6.3三角形的中位线(2) 课时练习
文档属性
| 名称 | 6.3三角形的中位线(2) 课时练习 |  | |
| 格式 | doc | ||
| 文件大小 | 168.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 09:47:36 | ||
图片预览

文档简介
新版北师大版八年级数学下册第6章《平行四边形》同步练习及答案—6.3三角形的中位线(2)
1.以三角形的一条中位线和第三边上的中线为对角线的四边形是( )
A.梯形 B.平行四边形 C.菱形 D.矩形
2.顺次连结等腰梯形两底的中点及两条对角线的中点,所组成的四边形是( )
A.菱形 B.平行四边形 C.矩形 D.直角三角形
3.如图所示,△ABC中,AH⊥BC于H,E、D、F分别是AB、BC、AC的中点,则四边形EDHF是( )
A.一般梯形 B.等腰梯形;
C.直角梯形 D.直角等腰梯形
4.梯形上底长为L,中位线长为m,则连结两条对角线中点的线段长为( )
A.m-2L B.-L C.2m-L D.m-L
5.若三角形的周长为56cm,则它的三条中位线组成的三角形的周长是_____.
6.等腰梯形的周长为80cm,它的中位线长等于腰长,则腰长为________.
7.梯形的中位线长为15cm,一条对角线把中位线分成3:2两部分,那么梯形的上底、下底的长分别是________和_______.
8.直角梯形的一腰与下底都等于a,这个腰与下底的夹角为60°,则中位线长为________.
新课标能力训练(每小题5分,共30分)
9.(学科内综合)等腰梯形的周长为66,腰长为8,对角线长为24,则连结两腰中点与一底中点的线段组成的三角形的周长为________.
10.如图所示,在直角梯形ABCD中,AB⊥BC,AD=1,BC=3,CD=4,EF为梯形中位线,DH为菱形的高.下列结论:(1)∠BCD=60°;(2)四边形EHCF为菱形;(3)S△BEH=S△CEH;(4)以AB为直径的圆与CD相切于F.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
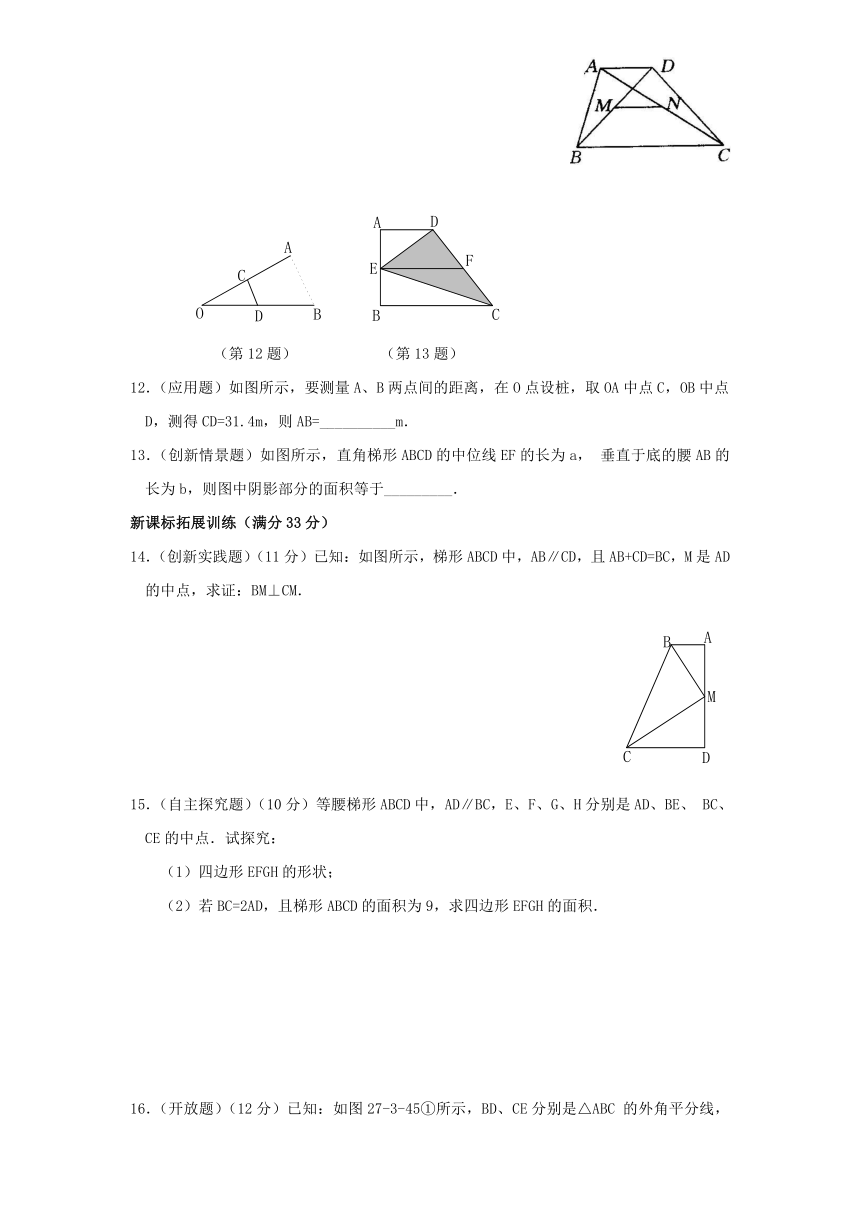
11.如图所示,已知梯形ABCD中,AD∥BC,且AD(第12题) (第13题)
12.(应用题)如图所示,要测量A、B两点间的距离,在O点设桩,取OA中点C,OB中点D,测得CD=31.4m,则AB=__________m. 来源:http://www./tiku/
13.(创新情景题)如图所示,直角梯形ABCD的中位线EF的长为a,垂直于底的腰AB的长为b,则图中阴影部分的面积等于_________.
新课标拓展训练(满分33分)
14.(创新实践题)(11分)已知:如图所示,梯形ABCD中,AB∥CD,且AB+CD=BC,M是AD的中点,求证:BM⊥CM.
15.(自主探究题)(10分)等腰梯形ABCD中,AD∥BC,E、F、G、H分别是AD、BE、BC、CE的中点.试探究:
(1)四边形EFGH的形状;
(2)若BC=2AD,且梯形ABCD的面积为9,求四边形EFGH的面积.
16.(开放题)(12分)已知:如图27-3-45①所示,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别为F、G.连结FG,延长AF、AG,与直线BC相交,易证FG=(AB+BC+AC).若(1)BD、CE分别是△ABC的内角平分线(如图②);(2)BD为△ABC的内角平分线,CE为△ABC的外角平分线(如图③),则在图②、图③两种情况下,线段FG与△ABC三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况给予证明. 来源:http://www./tiku/
参考答案:
1.B 2.A 3.B 4.D 5.28cm 6.20cm 7.12cm 18cm 8.a 9.49 10.C
11.取AB中点P,连MP,NP证N、M、P三点共线.
12.62.8
13.ab 解:如图所示,过点D作DG⊥EF于G,过点C作CH⊥EF交EF的延长线于H, 则DG+CH=AB=b.
故S阴影=S△DEF+S△CEF=EF·DG+EF·CH=EF(DG+CH)=ab.
点拨:本题通过巧作辅助线,运用三角形面积公式即可得到.
14.解:如图所示,延长BM交CD的延长线于点E.
∵AB∥CD,∴∠A=∠MDE(两直线平行,内错角相等).
在△ABM和△DEM中,∵∠A=∠MDE,AM=DM,∠AMB=DME,
∴△ABM≌△DEM(ASA).
∴BM=EM,AB=DE(全等三角形的对应边相等).
∵AB+CD=BC,
∴DE+DC=BC,即CE=CB.
∴CM⊥BM(等腰三角形底边中线也是底边上的高).
点拨:本题使用了“连结底的一端与所对腰的中点并延长与下底相交”的辅助线,构造了全等三角形.同时将梯形问题转化成了等腰三角形的问题.
15.解:∵梯形ABCD是等腰梯形,
∴AB=CD,∠A=∠D(等腰梯形的两腰相等,在同一底边上的两内角相等),
又∵AE=DE,
∴△ABE≌△DCE(SAS).
∴BE=CE(全等三角形的对应边相等).
又∵EF=EB,EH=EC,
∴EF=EH.
∵G、F、H分别是BC、BE、CE的中点,
∴GF∥CE,GH∥BE(三角形中位线定理).
∴四边形EFGH是平行四边形(平行四边形的定义).
∴EFGH是菱形(有一组邻边相等的平行四边形是菱形).
(2)∵BE=CE,G为BC中点,
∴EG⊥BC(等腰三角形的三线合一).
∴EG为梯形ABCD的高.
∵S梯形=(AD+BC)×EG=9,BC=2AD,
∴(BC+BC)×EG=9,
∴BC·EG=12.
∵F、H分别是BE、CE的中点,
∴FH=BC.
∴S菱形EFGH=FH·EG=××BC·EG=3.
点拨:通过三角形全等的性质得边相等,为求证四边形邻边相等创造条件.本题综合运用了等腰梯形的性质,平行四边形、菱形的判定、等腰三角形的性质以及三角形中位线定理、菱形的面积公式等.
16.解:猜想结果:图②中,FG=(AB+AC-BC);
图③中,FG=(BC+AC-AB).
证明图②的结果如下:
如图所示,分别延长AG、AF交BC于H、K.
在△ABF和△KBF中,
∵∠ABF=∠KBF,BF=BF,∠BFA=∠BFK=90°,
∴△ABF≌△KBF(ASA).
∴AF=FK,AB=BK(全等三角形的对应边相等).
同理△ACG≌△HCG.
∴AG=GH,AC=HC.
∴FG=HK(三角形中位数定理).
又∵HK=BK-BH=AB-(BC-CH)=AB-(BC-AC)=AB+AC-BC,
∴FG=(AB+AC-BC).
点拨:本题体现了类比的思想方法,综合运用全等三角形的判定及性质、三角形中位线定理解题.解题的关键是构造三角形的中位线.
1.以三角形的一条中位线和第三边上的中线为对角线的四边形是( )
A.梯形 B.平行四边形 C.菱形 D.矩形
2.顺次连结等腰梯形两底的中点及两条对角线的中点,所组成的四边形是( )
A.菱形 B.平行四边形 C.矩形 D.直角三角形
3.如图所示,△ABC中,AH⊥BC于H,E、D、F分别是AB、BC、AC的中点,则四边形EDHF是( )
A.一般梯形 B.等腰梯形;
C.直角梯形 D.直角等腰梯形
4.梯形上底长为L,中位线长为m,则连结两条对角线中点的线段长为( )
A.m-2L B.-L C.2m-L D.m-L
5.若三角形的周长为56cm,则它的三条中位线组成的三角形的周长是_____.
6.等腰梯形的周长为80cm,它的中位线长等于腰长,则腰长为________.
7.梯形的中位线长为15cm,一条对角线把中位线分成3:2两部分,那么梯形的上底、下底的长分别是________和_______.
8.直角梯形的一腰与下底都等于a,这个腰与下底的夹角为60°,则中位线长为________.
新课标能力训练(每小题5分,共30分)
9.(学科内综合)等腰梯形的周长为66,腰长为8,对角线长为24,则连结两腰中点与一底中点的线段组成的三角形的周长为________.
10.如图所示,在直角梯形ABCD中,AB⊥BC,AD=1,BC=3,CD=4,EF为梯形中位线,DH为菱形的高.下列结论:(1)∠BCD=60°;(2)四边形EHCF为菱形;(3)S△BEH=S△CEH;(4)以AB为直径的圆与CD相切于F.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
11.如图所示,已知梯形ABCD中,AD∥BC,且AD
12.(应用题)如图所示,要测量A、B两点间的距离,在O点设桩,取OA中点C,OB中点D,测得CD=31.4m,则AB=__________m. 来源:http://www./tiku/
13.(创新情景题)如图所示,直角梯形ABCD的中位线EF的长为a,垂直于底的腰AB的长为b,则图中阴影部分的面积等于_________.
新课标拓展训练(满分33分)
14.(创新实践题)(11分)已知:如图所示,梯形ABCD中,AB∥CD,且AB+CD=BC,M是AD的中点,求证:BM⊥CM.
15.(自主探究题)(10分)等腰梯形ABCD中,AD∥BC,E、F、G、H分别是AD、BE、BC、CE的中点.试探究:
(1)四边形EFGH的形状;
(2)若BC=2AD,且梯形ABCD的面积为9,求四边形EFGH的面积.
16.(开放题)(12分)已知:如图27-3-45①所示,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别为F、G.连结FG,延长AF、AG,与直线BC相交,易证FG=(AB+BC+AC).若(1)BD、CE分别是△ABC的内角平分线(如图②);(2)BD为△ABC的内角平分线,CE为△ABC的外角平分线(如图③),则在图②、图③两种情况下,线段FG与△ABC三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况给予证明. 来源:http://www./tiku/
参考答案:
1.B 2.A 3.B 4.D 5.28cm 6.20cm 7.12cm 18cm 8.a 9.49 10.C
11.取AB中点P,连MP,NP证N、M、P三点共线.
12.62.8
13.ab 解:如图所示,过点D作DG⊥EF于G,过点C作CH⊥EF交EF的延长线于H, 则DG+CH=AB=b.
故S阴影=S△DEF+S△CEF=EF·DG+EF·CH=EF(DG+CH)=ab.
点拨:本题通过巧作辅助线,运用三角形面积公式即可得到.
14.解:如图所示,延长BM交CD的延长线于点E.
∵AB∥CD,∴∠A=∠MDE(两直线平行,内错角相等).
在△ABM和△DEM中,∵∠A=∠MDE,AM=DM,∠AMB=DME,
∴△ABM≌△DEM(ASA).
∴BM=EM,AB=DE(全等三角形的对应边相等).
∵AB+CD=BC,
∴DE+DC=BC,即CE=CB.
∴CM⊥BM(等腰三角形底边中线也是底边上的高).
点拨:本题使用了“连结底的一端与所对腰的中点并延长与下底相交”的辅助线,构造了全等三角形.同时将梯形问题转化成了等腰三角形的问题.
15.解:∵梯形ABCD是等腰梯形,
∴AB=CD,∠A=∠D(等腰梯形的两腰相等,在同一底边上的两内角相等),
又∵AE=DE,
∴△ABE≌△DCE(SAS).
∴BE=CE(全等三角形的对应边相等).
又∵EF=EB,EH=EC,
∴EF=EH.
∵G、F、H分别是BC、BE、CE的中点,
∴GF∥CE,GH∥BE(三角形中位线定理).
∴四边形EFGH是平行四边形(平行四边形的定义).
∴EFGH是菱形(有一组邻边相等的平行四边形是菱形).
(2)∵BE=CE,G为BC中点,
∴EG⊥BC(等腰三角形的三线合一).
∴EG为梯形ABCD的高.
∵S梯形=(AD+BC)×EG=9,BC=2AD,
∴(BC+BC)×EG=9,
∴BC·EG=12.
∵F、H分别是BE、CE的中点,
∴FH=BC.
∴S菱形EFGH=FH·EG=××BC·EG=3.
点拨:通过三角形全等的性质得边相等,为求证四边形邻边相等创造条件.本题综合运用了等腰梯形的性质,平行四边形、菱形的判定、等腰三角形的性质以及三角形中位线定理、菱形的面积公式等.
16.解:猜想结果:图②中,FG=(AB+AC-BC);
图③中,FG=(BC+AC-AB).
证明图②的结果如下:
如图所示,分别延长AG、AF交BC于H、K.
在△ABF和△KBF中,
∵∠ABF=∠KBF,BF=BF,∠BFA=∠BFK=90°,
∴△ABF≌△KBF(ASA).
∴AF=FK,AB=BK(全等三角形的对应边相等).
同理△ACG≌△HCG.
∴AG=GH,AC=HC.
∴FG=HK(三角形中位数定理).
又∵HK=BK-BH=AB-(BC-CH)=AB-(BC-AC)=AB+AC-BC,
∴FG=(AB+AC-BC).
点拨:本题体现了类比的思想方法,综合运用全等三角形的判定及性质、三角形中位线定理解题.解题的关键是构造三角形的中位线.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
