1.2直角三角形（2） 课时练习

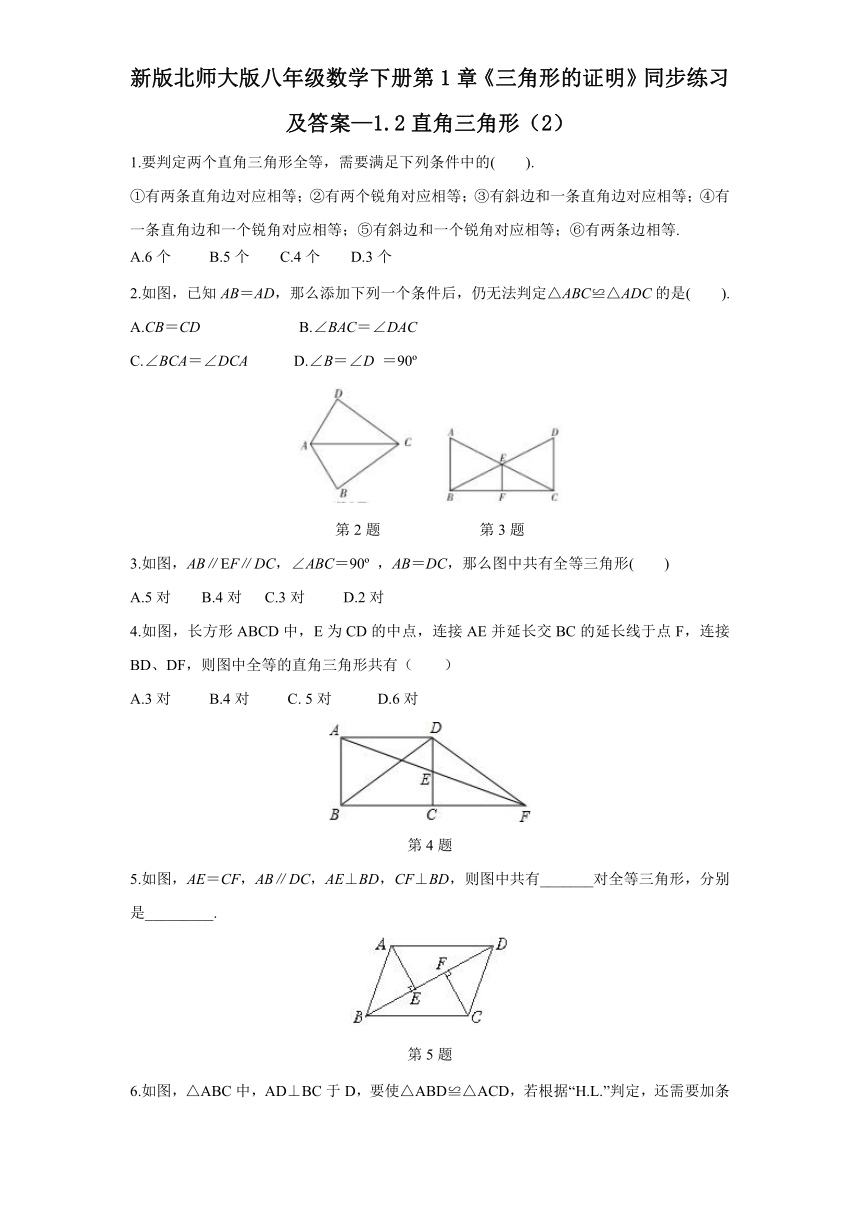
新版北师大版八年级数学下册第1章《三角形的证明》同步练习及答案—1.2直角三角形（2）
1.要判定两个直角三角形全等，需要满足下列条件中的( ).
①有两条直角边对应相等；②有两个锐角对应相等；③有斜边和一条直角边对应相等；④有一条直角边和一个锐角对应相等；⑤有斜边和一个锐角对应相等；⑥有两条边相等.
A.6个 B.5个 C.4个 D.3个
2.如图，已知AB＝AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是( ).
A.CB＝CD B.∠BAC＝∠DAC
C.∠BCA＝∠DCA D.∠B＝∠D ＝90
第2题 第3题
3.如图，AB∥EF∥DC，∠ABC＝90 ，AB＝DC，那么图中共有全等三角形( )
A.5对 B.4对 C.3对 D.2对
4.如图，长方形ABCD中，E为CD的中点，连接AE并延长交BC的延长线于点F，连接BD、DF，则图中全等的直角三角形共有（ ）
A.3对 B.4对 C. 5对 D.6对
第4题
5.如图，AE＝CF，AB∥DC，AE⊥BD，CF⊥BD，则图中共有_______对全等三角形，分别是_________.
第5题
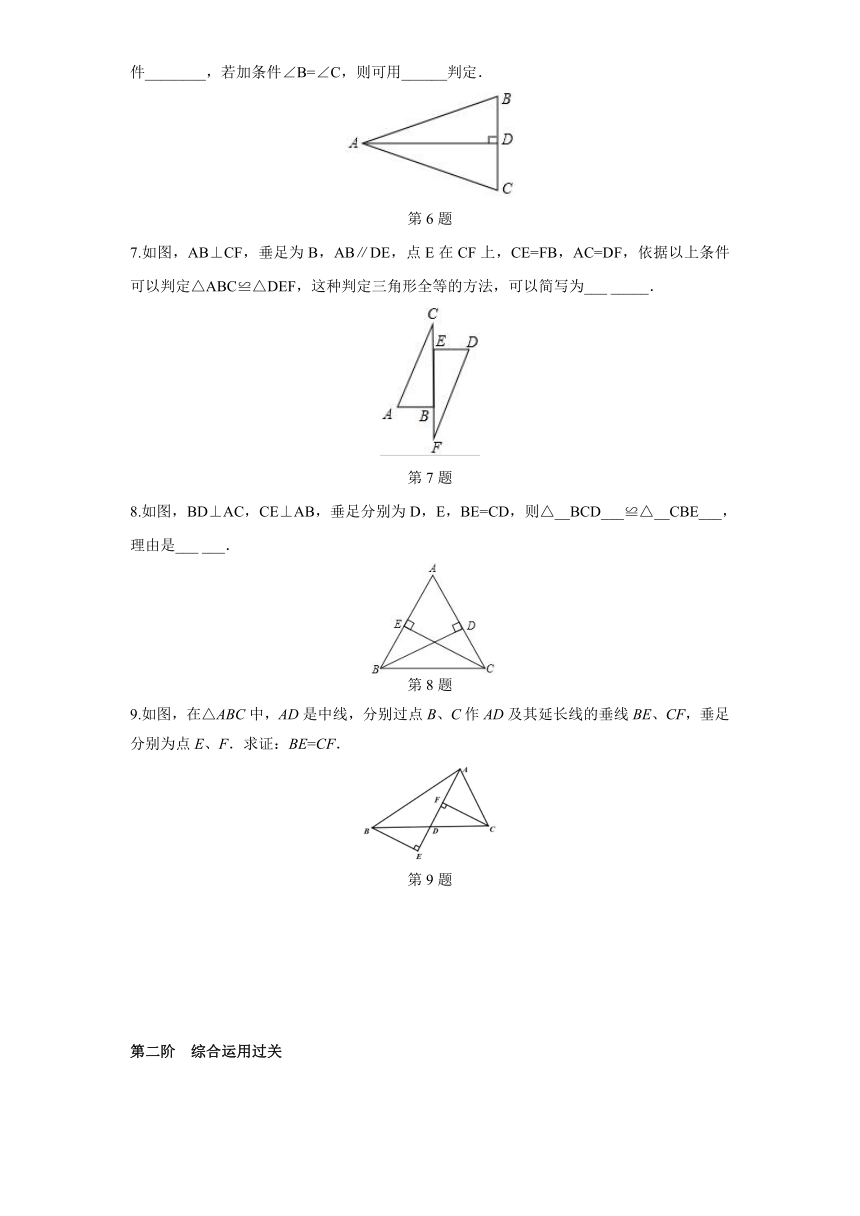
6.如图，△ABC中，AD⊥BC于D，要使△ABD≌△ACD，若根据“H.L.”判定，还需要加条件________，若加条件∠B=∠C，则可用______判定．
第6题
7.如图，AB⊥CF，垂足为B，AB∥DE，点E在CF上，CE=FB，AC=DF，依据以上条件可以判定△ABC≌△DEF，这种判定三角形全等的方法，可以简写为___ _____．
第7题
8.如图，BD⊥AC，CE⊥AB，垂足分别为D，E，BE=CD，则△__BCD___≌△__CBE___，理由是___ ___． 来源：http://www./tiku/
第8题
9.如图，在△ABC中，AD是中线，分别过点B、C作AD及其延长线的垂线BE、CF，垂足分别为点E、F．求证：BE=CF．
第9题
第二阶 综合运用过关
10．在△ABC中，AB=AC，D为AC上一点，且AD=BD，DE⊥AB于E，BD+DC=18，求AE的长.
第10题
11.如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连结BE、EC．
试猜想线段BE和EC的数量及位置关系，并证明你的猜想．
第11题
第三阶 思维能力拓展 来源：http://www./tiku/
12.如图所示,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD、CE相交于点F.
求证:∠BAF=∠CAF.
第12题
参考答案
1.C
2.C
3.C
4.B
5.3，（1）△ABE≌△CDF?（2）△ABD≌△CDB
（3）△AED≌△CFB．_.?
6. AB=AC，A.A.S.
7. H.L
8. H.L.
9.证明∵在△ABC中，AD是中线，∴BD=CD，∵CF⊥AD，BE⊥AD，∴∠CFD=∠BED=90° ，在△BED与△CFD中，∵∠BED=∠CFD，∠BDE=∠CDF，BD=CD，∴△BED≌△CFD(A.A.S.)，∴BE=CF.
10.解：∵DE⊥AB ∴∠AED=∠BED=∠90°，
又∵AD=BD，ED=ED,
∴Rt△BED≌Rt△AED(H.L.).
∴AE=EB.
又∵BD+DC=18 ,∴AD+DC=18 ∴AC=18.
又AB=AC=2AE,∴2AE=18 AE=9.
11.证明：BE=EC，BE⊥EC.
∵AC=2AB，点D是AC的中点，
∴AB=AD=CD.
∵∠EAD=∠EDA=45°，
∴∠EAB=∠EDC=135°.
∵EA=ED，∴△EAB≌△EDC，
∴∠AEB=∠DEC，EB=EC，
∴∠BEC=∠AED=90°，
∴BE=EC，BE⊥EC.
12.证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°.
∵AB=AC,∠BAD=∠CAE,∠ADB=∠AEC,
∴Rt△ABD≌Rt△ACE(A.A.S.).
∴AD=AE.
∵AD=AE,AF=AF, ∠ADF=∠AEF=90°,
∴Rt△ADF≌Rt△AEF(H.L.).
∴∠BAF=∠CAF(全等三角形对应角相等).