2022年苏科版七年级数学下册 第9章 数学活动 拼图·公式教案
文档属性
| 名称 | 2022年苏科版七年级数学下册 第9章 数学活动 拼图·公式教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 107.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 00:00:00 | ||
图片预览

文档简介
拼图·公式
教学目标:
1、进一步掌握长方形的拼图问题,会灵活的应用乘法公式和因式分解求出各类纸片的张数或长方形的边长。
2、进一步掌握完全平方公式和平方差公式,了解公式的几何背景,会灵活应用两个公式解决问题。
3、联系生活与实际,经历从具体问题抽象出数学问题——建立模型——综合运用已有的知识解决问题的过程。
4、获得一些研究问题的方法和经验,加深对知识的理解,发展有条理的思考和表达的能力。
教学重点:
1、进一步掌握长方形的拼图问题,会灵活的应用乘法公式和因式分解求出各类纸片的张数或长方形的边长。
2、进一步掌握完全平方公式和平方差公式,会灵活应用两个公式解决问题。
教学难点:
联系生活与实际,经历从具体问题抽象出数学问题——建立模型——综合运用已有的知识解决问题的过程。
例1.已知大长方形两边长,面积定,求各类纸片张数
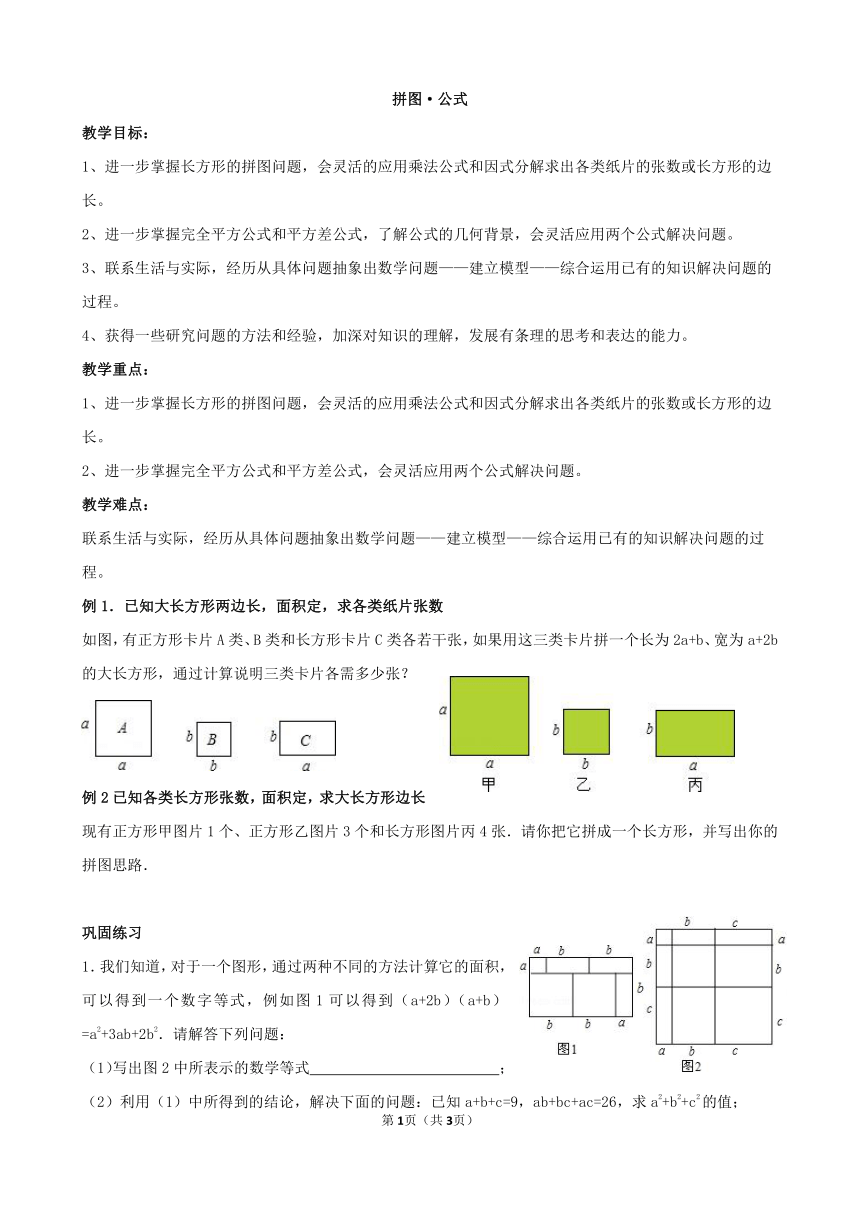
如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?
例2已知各类长方形张数,面积定,求大长方形边长
现有正方形甲图片1个、正方形乙图片3个和长方形图片丙4张.请你把它拼成一个长方形,并写出你的拼图思路.
巩固练习
1.我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数字等式,例如图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式 ;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=9,ab+bc+ac=26,求a2+b2+c2的值;
(3)小明同学用2张边长为a的正方形,3张边长为b的正方形,5张边长分别为a、b的长方形纸片拼出了一个长方形,那么该长方形较长一边的边长为多少?你能画出图形吗?
(4)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出了一个面积为(25a+7b)(2a+5b)长方形,那么9(x+y+z)= .
例3公式的应用①
图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1:
方法2:
(2)观察图2请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系.
;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;
②如果a,b(a>b>0)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
③已知:,求:的值.
(4)如图3,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
例4. 公式的应用②
(1)比较图3、4两图的阴影部分面积,可以得到乘法公式 (用式子表达).
(2)运用你所得到的公式计算:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
③(a+2b﹣c)(a﹣2b﹣c).
图1 图2
拓展与延伸:(生活与数学)
一个工程队要在一块长方形荒地上建造一套简易住房,如图所示,该住房的平面是由长2x+8、宽x+8构成,要求建成:两室、一厅、一厨、一卫,且各房间为长方形或正方形.其中客厅面积为x2+8x+16,卫生间面积为2x+8,厨房面积为x2+6x+8,主卧室的面积为4x+20,次卧面积为4x+12.若墙体所占面积忽略不计,请你根据所学知识,在所给图中设计一套住房的平面结构示意图.(要求:①在图上标出图中各房间的名称;②在图上用含有x的代数式表示图中各房间的边长)
巩固练习
2.如图,有A、B、C三种不同型号的卡片若干,其中A型是边长为a的正方形,B型是长为b,宽为a的矩形.C型是边长为b的正方形.
(1)请你选取相应型号和数量的卡片,在下图中的网格中拼出(或镶嵌)一个符合乘法公式的图形(要求三种型号的卡片都用上),这个乘法公式是 ;
(2)现有A型卡片1个,B型卡片6个,C型卡片10个,从这17个卡片中拿掉一个卡片,余下的卡片全用上,能拼出(或镶嵌)一个矩形(或正方形)的都是哪些情况?请你通过运算说明理由.
3.提出问题:怎么运用矩形面积表示与的大小关系(其中)?
几何建模:(1)画长,宽的矩形,按图方式分割(2)变形:
(3)分析:图中大矩形的面积可以表示为;阴影部分面积可以表示为,画点部分的面积可表示为,由图形的部分与整体的关系可知: >,即>
归纳提炼:当,时,表示与的大小关系根据题意,设,,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用铅笔画图,并标注相关线段的长)
第1页(共3页)
教学目标:
1、进一步掌握长方形的拼图问题,会灵活的应用乘法公式和因式分解求出各类纸片的张数或长方形的边长。
2、进一步掌握完全平方公式和平方差公式,了解公式的几何背景,会灵活应用两个公式解决问题。
3、联系生活与实际,经历从具体问题抽象出数学问题——建立模型——综合运用已有的知识解决问题的过程。
4、获得一些研究问题的方法和经验,加深对知识的理解,发展有条理的思考和表达的能力。
教学重点:
1、进一步掌握长方形的拼图问题,会灵活的应用乘法公式和因式分解求出各类纸片的张数或长方形的边长。
2、进一步掌握完全平方公式和平方差公式,会灵活应用两个公式解决问题。
教学难点:
联系生活与实际,经历从具体问题抽象出数学问题——建立模型——综合运用已有的知识解决问题的过程。
例1.已知大长方形两边长,面积定,求各类纸片张数
如图,有正方形卡片A类、B类和长方形卡片C类各若干张,如果用这三类卡片拼一个长为2a+b、宽为a+2b的大长方形,通过计算说明三类卡片各需多少张?
例2已知各类长方形张数,面积定,求大长方形边长
现有正方形甲图片1个、正方形乙图片3个和长方形图片丙4张.请你把它拼成一个长方形,并写出你的拼图思路.
巩固练习
1.我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数字等式,例如图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式 ;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=9,ab+bc+ac=26,求a2+b2+c2的值;
(3)小明同学用2张边长为a的正方形,3张边长为b的正方形,5张边长分别为a、b的长方形纸片拼出了一个长方形,那么该长方形较长一边的边长为多少?你能画出图形吗?
(4)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出了一个面积为(25a+7b)(2a+5b)长方形,那么9(x+y+z)= .
例3公式的应用①
图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1:
方法2:
(2)观察图2请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系.
;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;
②如果a,b(a>b>0)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
③已知:,求:的值.
(4)如图3,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
例4. 公式的应用②
(1)比较图3、4两图的阴影部分面积,可以得到乘法公式 (用式子表达).
(2)运用你所得到的公式计算:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
③(a+2b﹣c)(a﹣2b﹣c).
图1 图2
拓展与延伸:(生活与数学)
一个工程队要在一块长方形荒地上建造一套简易住房,如图所示,该住房的平面是由长2x+8、宽x+8构成,要求建成:两室、一厅、一厨、一卫,且各房间为长方形或正方形.其中客厅面积为x2+8x+16,卫生间面积为2x+8,厨房面积为x2+6x+8,主卧室的面积为4x+20,次卧面积为4x+12.若墙体所占面积忽略不计,请你根据所学知识,在所给图中设计一套住房的平面结构示意图.(要求:①在图上标出图中各房间的名称;②在图上用含有x的代数式表示图中各房间的边长)
巩固练习
2.如图,有A、B、C三种不同型号的卡片若干,其中A型是边长为a的正方形,B型是长为b,宽为a的矩形.C型是边长为b的正方形.
(1)请你选取相应型号和数量的卡片,在下图中的网格中拼出(或镶嵌)一个符合乘法公式的图形(要求三种型号的卡片都用上),这个乘法公式是 ;
(2)现有A型卡片1个,B型卡片6个,C型卡片10个,从这17个卡片中拿掉一个卡片,余下的卡片全用上,能拼出(或镶嵌)一个矩形(或正方形)的都是哪些情况?请你通过运算说明理由.
3.提出问题:怎么运用矩形面积表示与的大小关系(其中)?
几何建模:(1)画长,宽的矩形,按图方式分割(2)变形:
(3)分析:图中大矩形的面积可以表示为;阴影部分面积可以表示为,画点部分的面积可表示为,由图形的部分与整体的关系可知: >,即>
归纳提炼:当,时,表示与的大小关系根据题意,设,,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用铅笔画图,并标注相关线段的长)
第1页(共3页)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
