3.2圆的对称性(2) 课时练习
图片预览

文档简介
北师大版九年级数学下册课时同步练习-3.2圆的对称性(2)附答案
一.选择题(共10小题)
1.(2011 黄石)有如下图形:①函数y=x﹣1的图象;②函数的图象;③一段圆弧;④平行四边形.其中一定是轴对称图形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.(2013 徐州)如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为( )
A. 10 B. 8 C. 5 D. 3
3.(2013 内江)如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A. cm B. cm C. cm D. 4cm
4.(2013 牡丹江)在半径为13的⊙O中,弦AB∥CD,弦AB和CD的距离为7,若AB=24,则CD的长为( )
A. 10 B. 4 C. 10或4 D. 10或2
5.(2013 丽水)一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A. 4 B. 5 C. 6 D. 8
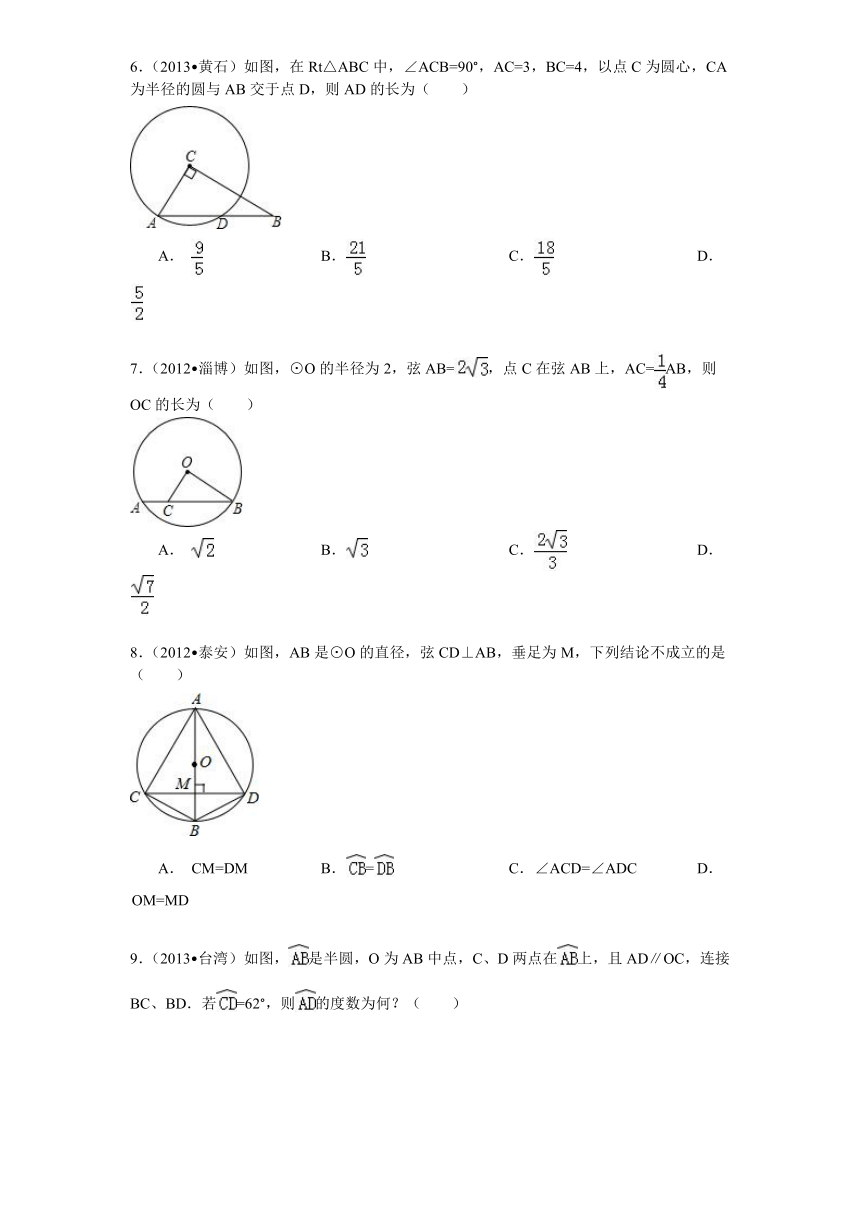
6.(2013 黄石)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A. B. C. D.
7.(2012 淄博)如图,⊙O的半径为2,弦AB=,点C在弦AB上,AC=AB,则OC的长为( )
A. B. C. D.
8.(2012 泰安)如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A. CM=DM B. = C. ∠ACD=∠ADC D. OM=MD
9.(2013 台湾)如图,是半圆,O为AB中点,C、D两点在上,且AD∥OC,连接BC、BD.若=62°,则的度数为何?( )
A. 56 B. 58 C. 60 D. 62
10.(2013 乐山)如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点.则弦CD长的所有可能的整数值有( )
A. 1个 B. 2个 C. 3个 D. 4个
二.填空题(共10小题)
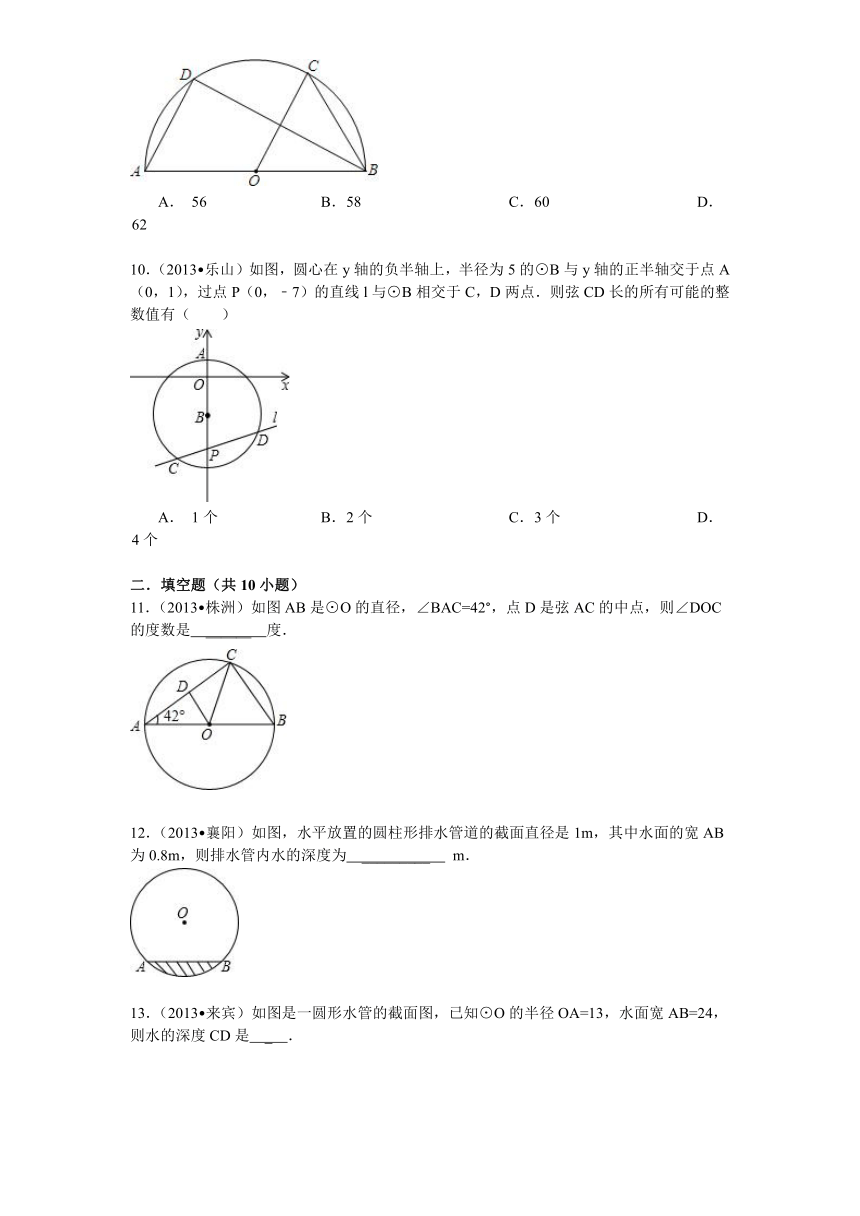
11.(2013 株洲)如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是 ______ 度.
12.(2013 襄阳)如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为 _________ m.
13.(2013 来宾)如图是一圆形水管的截面图,已知⊙O的半径OA=13,水面宽AB=24,则水的深度CD是 _ .
14.(2013 广州)如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为 _________ .
15.(2012 珠海)如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=26,CD=24,那么sin∠OCE= .
16.(2012 嘉兴)如图,在⊙O中,直径AB丄弦CD于点M,AM=18,BM=8,则CD的长为 ____ .
17.(2011 永州)如图,在⊙O中,直径CD垂直弦AB于点E,连接OB,CB,已知⊙O的半径为2,AB=,则∠BCD= _________ 度.
18.(2013 扬州)如图,已知⊙O的直径AB=6,E、F为AB的三等分点,M、N为上两点,且∠MEB=∠NFB=60°,则EM+FN= _________ .
19.(2013 西宁)如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3,则AB= _.
20.(2013 吉林)如图,AB是⊙O的弦,OC⊥AB于点C,连接OA、OB.点P是半径OB上任意一点,连接AP.若OA=5cm,OC=3cm,则AP的长度可能是 _________ cm(写出一个符合条件的数值即可)
三.解答题(共4小题)
21.(2013 大庆)如图,平面直角坐标系中,以点C(2,)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
22.(2012 南通)如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离.
23.(2011 资阳)如图,A、B、C、D、E、F是⊙O的六等分点.
(1)连接AB、AD、AF,求证:AB+AF=AD;
(2)若P是圆周上异于已知六等分点的动点,连接PB、PD、PF,写出这三条线段长度的数量关系(不必说明理由).
24.(2012 雅安)已知⊙O的弦CD与直径AB垂直于F,点E在CD上,且AE=CE.
(1)求证:CA2=CE CD;
(2)已知CA=5,EA=3,求sin∠EAF.
参考答案
一.选择题(共10小题)
1. C.2. C.3. A.4. D.5. C.6. C.7. D.8. D9. A.10. C.
二.填空题(共10小题)
11. 48.12. 0.2.13. 8.14.(3,2).15. .16. 24.17. 30.18. .19. 4
20. 6.
三.解答题(共4小题)
21.解:(1)过点C作CM⊥x轴于点M,则MA=MB,连结AC,如图∵点C的坐标为(2,),∴OM=2,CM=,在Rt△ACM中,CA=2,∴AM==1,∴OA=OM﹣AM=1,OB=OM+BM=3,∴A点坐标为(1,0),B点坐标为(3,0);
(2)将A(1,0),B(3,0)代入y=x2+bx+c得,解得.
所以二次函数的解析式为y=x2﹣4x+3.
22.解:过点O作弦AB的垂线,垂足为E,延长OE交CD于点F,连接OA,OC,∵AB∥CD,∴OF⊥CD,∵AB=30cm,CD=16cm,∴AE=AB=×30=15cm,CF=CD=×16=8cm,在Rt△AOE中,OE===8cm,在Rt△OCF中,OF===15cm,∴EF=OF﹣OE=15﹣8=7cm.
答:AB和CD的距离为7cm.
23.解:(1)连接OB、OF.∵A、B、C、D、E、F是⊙O的六等分点,∴AD是⊙O的直径,且∠AOB=∠AOF=60°,∴△AOB、△AOF是等边三角形.∴AB=AF=AO=OD,∴AB+AF=AD.
(2)当P在上时,PB+PF=PD;当P在上时,PB+PD=PF;当P在上时,PD+PF=PB.
24.(1)证明:在△CEA和△CAD中,
∵弦CD⊥直径AB,∴=,∴∠D=∠C,又∵AE=EC,∴∠CAE=∠C,∴∠CAE=∠D,∵∠C是公共角,∴△CEA∽△CAD,∴,即CA2=CE CD;
(2)解:∵CA2=CE CD,AC=5,EC=3,∴52=CD 3,解得:CD=,又∵CF=FD,∴CF=CD=×=,∴EF=CF﹣CE=﹣3=,在Rt△AFE中,sin∠EAF=.
一.选择题(共10小题)
1.(2011 黄石)有如下图形:①函数y=x﹣1的图象;②函数的图象;③一段圆弧;④平行四边形.其中一定是轴对称图形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.(2013 徐州)如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为( )
A. 10 B. 8 C. 5 D. 3
3.(2013 内江)如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A. cm B. cm C. cm D. 4cm
4.(2013 牡丹江)在半径为13的⊙O中,弦AB∥CD,弦AB和CD的距离为7,若AB=24,则CD的长为( )
A. 10 B. 4 C. 10或4 D. 10或2
5.(2013 丽水)一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A. 4 B. 5 C. 6 D. 8
6.(2013 黄石)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A. B. C. D.
7.(2012 淄博)如图,⊙O的半径为2,弦AB=,点C在弦AB上,AC=AB,则OC的长为( )
A. B. C. D.
8.(2012 泰安)如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A. CM=DM B. = C. ∠ACD=∠ADC D. OM=MD
9.(2013 台湾)如图,是半圆,O为AB中点,C、D两点在上,且AD∥OC,连接BC、BD.若=62°,则的度数为何?( )
A. 56 B. 58 C. 60 D. 62
10.(2013 乐山)如图,圆心在y轴的负半轴上,半径为5的⊙B与y轴的正半轴交于点A(0,1),过点P(0,﹣7)的直线l与⊙B相交于C,D两点.则弦CD长的所有可能的整数值有( )
A. 1个 B. 2个 C. 3个 D. 4个
二.填空题(共10小题)
11.(2013 株洲)如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是 ______ 度.
12.(2013 襄阳)如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为 _________ m.
13.(2013 来宾)如图是一圆形水管的截面图,已知⊙O的半径OA=13,水面宽AB=24,则水的深度CD是 _ .
14.(2013 广州)如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为 _________ .
15.(2012 珠海)如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=26,CD=24,那么sin∠OCE= .
16.(2012 嘉兴)如图,在⊙O中,直径AB丄弦CD于点M,AM=18,BM=8,则CD的长为 ____ .
17.(2011 永州)如图,在⊙O中,直径CD垂直弦AB于点E,连接OB,CB,已知⊙O的半径为2,AB=,则∠BCD= _________ 度.
18.(2013 扬州)如图,已知⊙O的直径AB=6,E、F为AB的三等分点,M、N为上两点,且∠MEB=∠NFB=60°,则EM+FN= _________ .
19.(2013 西宁)如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3,则AB= _.
20.(2013 吉林)如图,AB是⊙O的弦,OC⊥AB于点C,连接OA、OB.点P是半径OB上任意一点,连接AP.若OA=5cm,OC=3cm,则AP的长度可能是 _________ cm(写出一个符合条件的数值即可)
三.解答题(共4小题)
21.(2013 大庆)如图,平面直角坐标系中,以点C(2,)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
22.(2012 南通)如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离.
23.(2011 资阳)如图,A、B、C、D、E、F是⊙O的六等分点.
(1)连接AB、AD、AF,求证:AB+AF=AD;
(2)若P是圆周上异于已知六等分点的动点,连接PB、PD、PF,写出这三条线段长度的数量关系(不必说明理由).
24.(2012 雅安)已知⊙O的弦CD与直径AB垂直于F,点E在CD上,且AE=CE.
(1)求证:CA2=CE CD;
(2)已知CA=5,EA=3,求sin∠EAF.
参考答案
一.选择题(共10小题)
1. C.2. C.3. A.4. D.5. C.6. C.7. D.8. D9. A.10. C.
二.填空题(共10小题)
11. 48.12. 0.2.13. 8.14.(3,2).15. .16. 24.17. 30.18. .19. 4
20. 6.
三.解答题(共4小题)
21.解:(1)过点C作CM⊥x轴于点M,则MA=MB,连结AC,如图∵点C的坐标为(2,),∴OM=2,CM=,在Rt△ACM中,CA=2,∴AM==1,∴OA=OM﹣AM=1,OB=OM+BM=3,∴A点坐标为(1,0),B点坐标为(3,0);
(2)将A(1,0),B(3,0)代入y=x2+bx+c得,解得.
所以二次函数的解析式为y=x2﹣4x+3.
22.解:过点O作弦AB的垂线,垂足为E,延长OE交CD于点F,连接OA,OC,∵AB∥CD,∴OF⊥CD,∵AB=30cm,CD=16cm,∴AE=AB=×30=15cm,CF=CD=×16=8cm,在Rt△AOE中,OE===8cm,在Rt△OCF中,OF===15cm,∴EF=OF﹣OE=15﹣8=7cm.
答:AB和CD的距离为7cm.
23.解:(1)连接OB、OF.∵A、B、C、D、E、F是⊙O的六等分点,∴AD是⊙O的直径,且∠AOB=∠AOF=60°,∴△AOB、△AOF是等边三角形.∴AB=AF=AO=OD,∴AB+AF=AD.
(2)当P在上时,PB+PF=PD;当P在上时,PB+PD=PF;当P在上时,PD+PF=PB.
24.(1)证明:在△CEA和△CAD中,
∵弦CD⊥直径AB,∴=,∴∠D=∠C,又∵AE=EC,∴∠CAE=∠C,∴∠CAE=∠D,∵∠C是公共角,∴△CEA∽△CAD,∴,即CA2=CE CD;
(2)解:∵CA2=CE CD,AC=5,EC=3,∴52=CD 3,解得:CD=,又∵CF=FD,∴CF=CD=×=,∴EF=CF﹣CE=﹣3=,在Rt△AFE中,sin∠EAF=.
