3.7弧长及扇形的面积(2) 课时练习
文档属性
| 名称 | 3.7弧长及扇形的面积(2) 课时练习 |  | |
| 格式 | doc | ||
| 文件大小 | 425.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 10:30:07 | ||
图片预览

文档简介
北师大版九年级数学下册课时同步练习-3.7弧长及扇形的面积(2)附答案
一、请准确填空(每小题3分,共24分)
1.两个同心圆的半径差为5,其中一个圆的周长为15π,则另一个圆的周长为_____.
2.已知a、b、c分别是正六边形的一边、最短对角线和最长对角线,则a∶b∶c为_____.
3.已知Rt△ABC,斜边AB=13 cm,以直线BC为轴旋转一周,得到一个侧面积为65π cm2的圆锥,则这个圆锥的高等于_____.
4.已知在同一平面内圆锥两母线在顶点最大的夹角为60°,母线长为8,则圆锥的侧面积为_____
5.已知圆柱的底面半径长和母线长是方程4x2-11x+2=0的两个根,则该圆柱的侧面展开图的面积是_____.
6.圆内接正方形的一边切下的一部分的面积等于2π-4,则正方形的边长是_____,这个正方形的内切圆半径是_____.
7.要制造一个圆锥形的烟囱帽,如图1,使底面半径r与母线l的比r∶l=3∶4,那么在剪扇形铁皮时,圆心角应取_____.
8.将一根长24 cm的筷子,置于底面直径为5 cm,高为12 cm的圆柱形水杯中(如图2).设筷子露在杯子外面的长为h cm,则h的取值范围是_____.
图1 图2
二、相信你的选择(每小题3分,共24分)
9.已知正三角形的边长为a,其内切圆的半径为r,外接圆的半径为R,则r∶a∶R等于
A.1∶2∶2 B.1∶2∶2 C.1∶2∶ D.1∶∶2
10.如图3,△ABC是正三角形,曲线ABCDEF…叫做“正三角形的渐开线”,其中、 ?、? 、…?圆心依次按A、B、C循环,它们依次相连接,如果AB=1,那么曲线CDEF的长是
A.8π B.6π C.4π D.2π
11.如图4,一扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30 cm,贴纸部分BD长为20 cm,贴纸部分的面积为
A.800π cm2 B.500π cm2 C.π cm2 D.π cm2
12.已知如图5,两同心圆中大圆的半径OA、OB交小圆于C、D,OC∶CA=3∶2,则和的长度比为
A.1∶1 B.3∶2 C.3∶5 D.9∶25
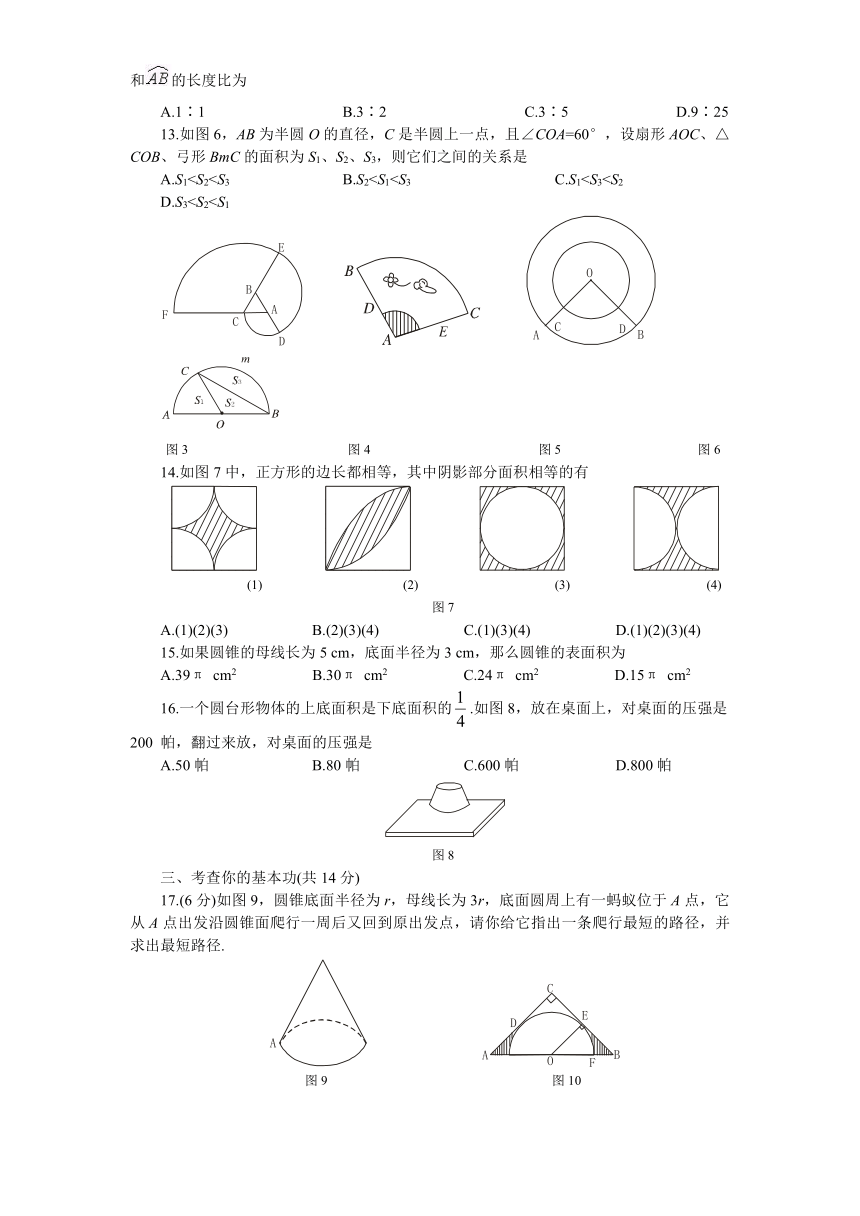
13.如图6,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3,则它们之间的关系是
A.S1图3 图4 图5 图6
14.如图7中,正方形的边长都相等,其中阴影部分面积相等的有
(1) (2) (3) (4)
图7
A.(1)(2)(3) B.(2)(3)(4) C.(1)(3)(4) D.(1)(2)(3)(4)
15.如果圆锥的母线长为5 cm,底面半径为3 cm,那么圆锥的表面积为
A.39π cm2 B.30π cm2 C.24π cm2 D.15π cm2
16.一个圆台形物体的上底面积是下底面积的.如图8,放在桌面上,对桌面的压强是200 帕,翻过来放,对桌面的压强是
A.50帕 B.80帕 C.600帕 D.800帕
图8
三、考查你的基本功(共14分)
17.(6分)如图9,圆锥底面半径为r,母线长为3r,底面圆周上有一蚂蚁位于A点,它从A点出发沿圆锥面爬行一周后又回到原出发点,请你给它指出一条爬行最短的路径,并求出最短路径.
图9 图10
18.(8分)如图10,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)
四、生活中的数学(共18分)
19.(8分)铅球比赛要求运动员在一固定圆圈内投掷,推出的铅球必须落在40°角的扇形区域内(以投掷圈的中心为圆心).如果运动员最多可投7 m,那么这一比赛的安全区域的面积至少应是多少?(结果精确到0.1 m2)
20.(10分)如图11,有一直径是1 m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形CAB.
(1)被剪掉的阴影部分的面积是多少?
(2)若用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?(结果可用根号表示)
图11 图12 图13
五、探究拓展与应用(共20分)
21.(10分)现有总长为8 m的建筑材料,用这些建筑材料围成一个扇形的花坛(如图12),当这个扇形的半径为多少时,可以使这个扇形花坛的面积最大?并求最大面积.
22.(10分)如图13,正三角形ABC的中心恰好为扇形ODE的圆心,且点B在扇形内,要使扇形ODE绕点O无论怎样转动,△ABC与扇形重叠部分的面积总等于△ABC的面积的,扇形的圆心角应为多少度?说明你的理由.
参考答案
一、1.5π或25π 2.1∶∶2 3.12 cm 4.32π 5.π 6.4 2 7.270° 8.11≤h≤12
二、9.A 10.C 11.C 12.C 13.B 14.C 15.C 16.D
三、17.解:把圆锥沿过点A的母线展成如图所示扇形,则蚂蚁运动的最短路程为AA′(线段).
由此知:OA=OA′=3r, 的长为2πr.
∴2πr=, n=120°,
即∠AOA′=120°, ∠OAC=30°.
∴.
∴. ∴AA′=2AC=3r,
即蚂蚁运动的最短路程是3r.
18.解:AC=ABcos45°=2,连接OE.
∴OE⊥BC , OE∥AC.
又OA=OB,则OE=BE=EC=AC=,
S阴影=2(S△OBE-S扇形OEF)=2-.
四、19.解:S扇形=≈17.2 m2.
20.(1)连接AB,则AB为⊙O直径.
∴S阴影=S⊙O-S扇形ABC=π·()2-π·(cm2).
(2)设所剪成圆锥的底面圆的半径为r,
则2πr=, ∴r=(m).
五、21.解:设扇形的半径为r,∠AOB的度数为n,扇形花坛面积为S,则扇形花坛周长为
2r+·2πr=8, ①
S=πr2. ②
由①得:. ③
将③代入②得:S=·πr2=4r-r2=-(r-2)2+4.
故当r=2时,S最大=4,
即当扇形半径为2 m时,花坛面积最大,其最大面积为4 m2.
22.当扇形的圆心角为120°时,△ABC与扇形重合部分的面积为△ABC面积的,无论绕点O怎样旋转,重合部分都等于△OAB的面积.
连接OB、OC,∴S△OBC=S△ABC .
∵∠BOC=120°,∠OBC=∠OCB=30°.
当∠DOE=120°时,
扇形ODE的两条半径OD、OE分别与OB、OC重合时,重合部分的面积为S△OBC .
当OD、OE不与OB、OC重合时,设OD交AB于点G,OE交BC于点H,
则∠BOG=∠COH,OB=OC, ∠OBG=∠OCH=30°.
∴△OBG≌△OCH .
∴S△OBG+S△OBH=S△OCH+S△OBH ,
即S四边形OGBH=S△OBC=S△ABC .
EF
DE
一、请准确填空(每小题3分,共24分)
1.两个同心圆的半径差为5,其中一个圆的周长为15π,则另一个圆的周长为_____.
2.已知a、b、c分别是正六边形的一边、最短对角线和最长对角线,则a∶b∶c为_____.
3.已知Rt△ABC,斜边AB=13 cm,以直线BC为轴旋转一周,得到一个侧面积为65π cm2的圆锥,则这个圆锥的高等于_____.
4.已知在同一平面内圆锥两母线在顶点最大的夹角为60°,母线长为8,则圆锥的侧面积为_____
5.已知圆柱的底面半径长和母线长是方程4x2-11x+2=0的两个根,则该圆柱的侧面展开图的面积是_____.
6.圆内接正方形的一边切下的一部分的面积等于2π-4,则正方形的边长是_____,这个正方形的内切圆半径是_____.
7.要制造一个圆锥形的烟囱帽,如图1,使底面半径r与母线l的比r∶l=3∶4,那么在剪扇形铁皮时,圆心角应取_____.
8.将一根长24 cm的筷子,置于底面直径为5 cm,高为12 cm的圆柱形水杯中(如图2).设筷子露在杯子外面的长为h cm,则h的取值范围是_____.
图1 图2
二、相信你的选择(每小题3分,共24分)
9.已知正三角形的边长为a,其内切圆的半径为r,外接圆的半径为R,则r∶a∶R等于
A.1∶2∶2 B.1∶2∶2 C.1∶2∶ D.1∶∶2
10.如图3,△ABC是正三角形,曲线ABCDEF…叫做“正三角形的渐开线”,其中、 ?、? 、…?圆心依次按A、B、C循环,它们依次相连接,如果AB=1,那么曲线CDEF的长是
A.8π B.6π C.4π D.2π
11.如图4,一扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30 cm,贴纸部分BD长为20 cm,贴纸部分的面积为
A.800π cm2 B.500π cm2 C.π cm2 D.π cm2
12.已知如图5,两同心圆中大圆的半径OA、OB交小圆于C、D,OC∶CA=3∶2,则和的长度比为
A.1∶1 B.3∶2 C.3∶5 D.9∶25
13.如图6,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3,则它们之间的关系是
A.S1
14.如图7中,正方形的边长都相等,其中阴影部分面积相等的有
(1) (2) (3) (4)
图7
A.(1)(2)(3) B.(2)(3)(4) C.(1)(3)(4) D.(1)(2)(3)(4)
15.如果圆锥的母线长为5 cm,底面半径为3 cm,那么圆锥的表面积为
A.39π cm2 B.30π cm2 C.24π cm2 D.15π cm2
16.一个圆台形物体的上底面积是下底面积的.如图8,放在桌面上,对桌面的压强是200 帕,翻过来放,对桌面的压强是
A.50帕 B.80帕 C.600帕 D.800帕
图8
三、考查你的基本功(共14分)
17.(6分)如图9,圆锥底面半径为r,母线长为3r,底面圆周上有一蚂蚁位于A点,它从A点出发沿圆锥面爬行一周后又回到原出发点,请你给它指出一条爬行最短的路径,并求出最短路径.
图9 图10
18.(8分)如图10,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)
四、生活中的数学(共18分)
19.(8分)铅球比赛要求运动员在一固定圆圈内投掷,推出的铅球必须落在40°角的扇形区域内(以投掷圈的中心为圆心).如果运动员最多可投7 m,那么这一比赛的安全区域的面积至少应是多少?(结果精确到0.1 m2)
20.(10分)如图11,有一直径是1 m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形CAB.
(1)被剪掉的阴影部分的面积是多少?
(2)若用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?(结果可用根号表示)
图11 图12 图13
五、探究拓展与应用(共20分)
21.(10分)现有总长为8 m的建筑材料,用这些建筑材料围成一个扇形的花坛(如图12),当这个扇形的半径为多少时,可以使这个扇形花坛的面积最大?并求最大面积.
22.(10分)如图13,正三角形ABC的中心恰好为扇形ODE的圆心,且点B在扇形内,要使扇形ODE绕点O无论怎样转动,△ABC与扇形重叠部分的面积总等于△ABC的面积的,扇形的圆心角应为多少度?说明你的理由.
参考答案
一、1.5π或25π 2.1∶∶2 3.12 cm 4.32π 5.π 6.4 2 7.270° 8.11≤h≤12
二、9.A 10.C 11.C 12.C 13.B 14.C 15.C 16.D
三、17.解:把圆锥沿过点A的母线展成如图所示扇形,则蚂蚁运动的最短路程为AA′(线段).
由此知:OA=OA′=3r, 的长为2πr.
∴2πr=, n=120°,
即∠AOA′=120°, ∠OAC=30°.
∴.
∴. ∴AA′=2AC=3r,
即蚂蚁运动的最短路程是3r.
18.解:AC=ABcos45°=2,连接OE.
∴OE⊥BC , OE∥AC.
又OA=OB,则OE=BE=EC=AC=,
S阴影=2(S△OBE-S扇形OEF)=2-.
四、19.解:S扇形=≈17.2 m2.
20.(1)连接AB,则AB为⊙O直径.
∴S阴影=S⊙O-S扇形ABC=π·()2-π·(cm2).
(2)设所剪成圆锥的底面圆的半径为r,
则2πr=, ∴r=(m).
五、21.解:设扇形的半径为r,∠AOB的度数为n,扇形花坛面积为S,则扇形花坛周长为
2r+·2πr=8, ①
S=πr2. ②
由①得:. ③
将③代入②得:S=·πr2=4r-r2=-(r-2)2+4.
故当r=2时,S最大=4,
即当扇形半径为2 m时,花坛面积最大,其最大面积为4 m2.
22.当扇形的圆心角为120°时,△ABC与扇形重合部分的面积为△ABC面积的,无论绕点O怎样旋转,重合部分都等于△OAB的面积.
连接OB、OC,∴S△OBC=S△ABC .
∵∠BOC=120°,∠OBC=∠OCB=30°.
当∠DOE=120°时,
扇形ODE的两条半径OD、OE分别与OB、OC重合时,重合部分的面积为S△OBC .
当OD、OE不与OB、OC重合时,设OD交AB于点G,OE交BC于点H,
则∠BOG=∠COH,OB=OC, ∠OBG=∠OCH=30°.
∴△OBG≌△OCH .
∴S△OBG+S△OBH=S△OCH+S△OBH ,
即S四边形OGBH=S△OBC=S△ABC .
EF
DE
