5.1.1 相交线 课时练习
图片预览
文档简介
第五章 相交线与平行线
5.1 相交线
5.1.1 相交线
要点感知1 有一条公共边,另一边__________,具有这种位置关系的两个角互为邻补角.
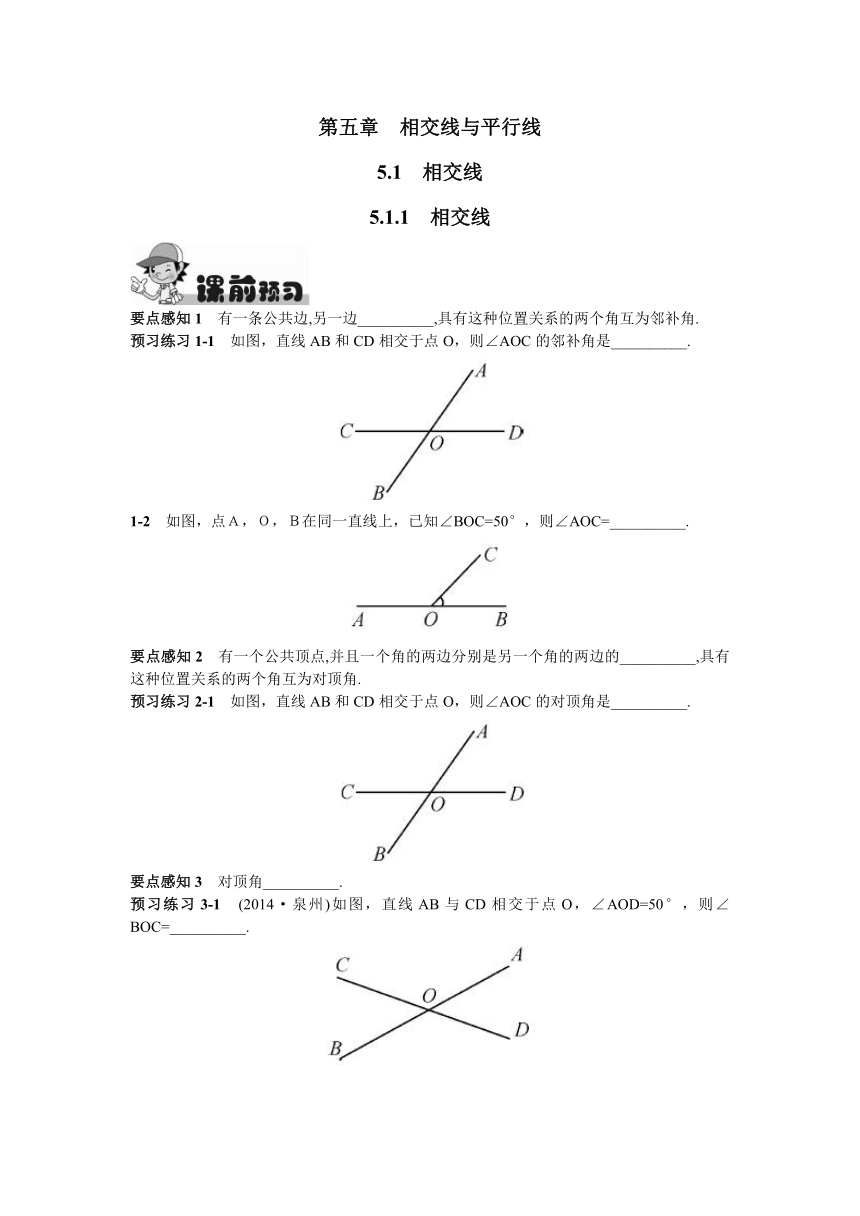
预习练习1-1 如图,直线AB和CD相交于点O,则∠AOC的邻补角是__________.
1-2 如图,点A,O,B在同一直线上,已知∠BOC=50°,则∠AOC=__________.
要点感知2 有一个公共顶点,并且一个角的两边分别是另一个角的两边的__________,具有这种位置关系的两个角互为对顶角.
预习练习2-1 如图,直线AB和CD相交于点O,则∠AOC的对顶角是__________.
要点感知3 对顶角__________.
预习练习3-1 (2014·泉州)如图,直线AB与CD相交于点O,∠AOD=50°,则∠BOC=__________.
知识点1 认识对顶角和邻补角
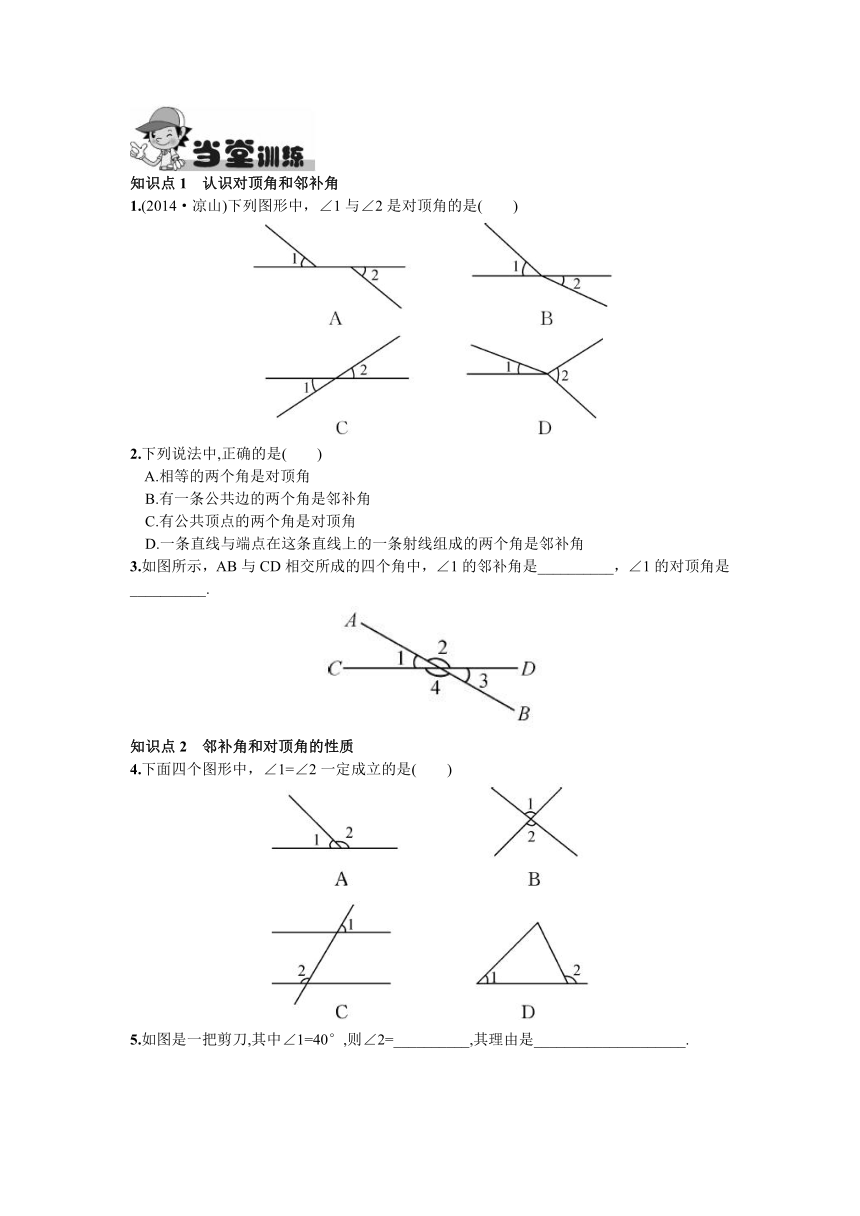
1.(2014·凉山)下列图形中,∠1与∠2是对顶角的是( )
2.下列说法中,正确的是( )
A.相等的两个角是对顶角
B.有一条公共边的两个角是邻补角
C.有公共顶点的两个角是对顶角
D.一条直线与端点在这条直线上的一条射线组成的两个角是邻补角
3.如图所示,AB与CD相交所成的四个角中,∠1的邻补角是__________,∠1的对顶角是__________.
知识点2 邻补角和对顶角的性质
4.下面四个图形中,∠1=∠2一定成立的是( )
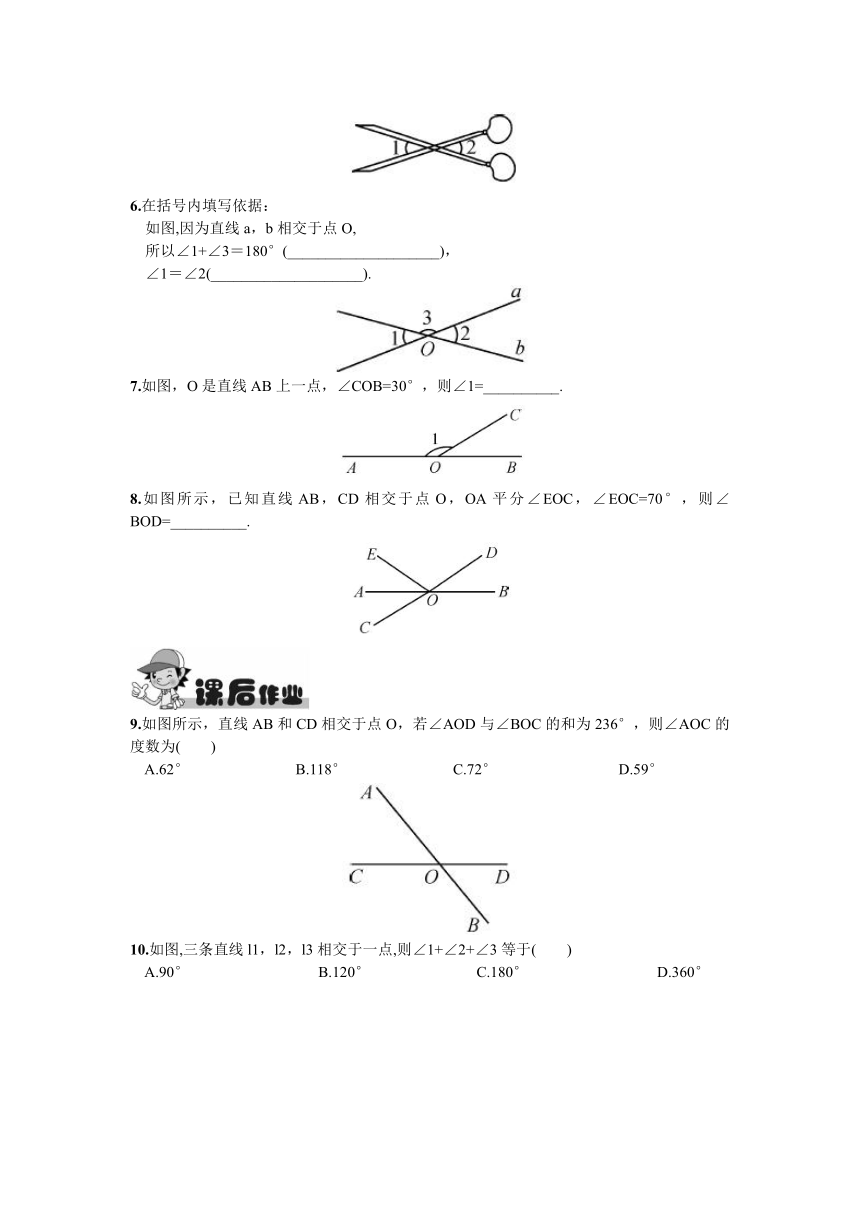
5.如图是一把剪刀,其中∠1=40°,则∠2=__________,其理由是____________________.
6.在括号内填写依据:
如图,因为直线a,b相交于点O,
所以∠1+∠3=180°(____________________),
∠1=∠2(____________________).
7.如图,O是直线AB上一点,∠COB=30°,则∠1=__________.
8.如图所示,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD=__________.
9.如图所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( )
A.62° B.118° C.72° D.59°
10.如图,三条直线l1,l2,l3相交于一点,则∠1+∠2+∠3等于( )
A.90° B.120° C.180° D.360°
11.(2013·大连)如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
12.如图,若∠1+∠3=180°,则图中与∠1相等的角有__________个,与∠1互补的角有__________个.
13.如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4=__________.
14.如图所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD-∠DOB=60°,则∠EOB=__________.
15.如图所示,AB,CD,EF交于点O,∠1=20°,∠2=60°,求∠BOC的度数.
16.如图所示,直线AB与CD相交于点O,OE平分∠AOD,∠BOC=80°,求∠BOD和∠AOE的度数.
17.如图所示,l1,l2,l3交于点O,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.
挑战自我
18.探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
参考答案
课前预习
要点感知1 互为反向延长线
预习练习1-1 ∠AOD和∠BOC
1-2 130°
要点感知2 反向延长线
预习练习2-1 ∠BOD
要点感知3 相等
预习练习3-1 50°
当堂训练
1.C 2.D 3.∠2,∠4∠3
4.B 5.40° 对顶角相等 6.邻补角互补 对顶角相等 7.150° 8.35°
课后作业
9.A 10.C 11.C 12.34 13.140° 14.150°
15.因为∠BOF=∠2=60°,
所以∠BOC=∠1+∠BOF=20°+60°=80°.
16.因为∠BOD与∠BOC是邻补角,∠BOC=80°,
所以∠BOD=180°—∠BOC=100°.
又因为∠AOD与∠BOC是对顶角,
所以∠AOD=∠BOC=80°.
又因为OE平分∠AOD,
所以∠AOE=∠BOC=40°.
17.设∠1=∠2=x°,则∠3=8x°.
由∠1+∠2+∠3=180°,得
10x=180.解得x=18.
所以∠1=∠2=18°.
所以∠4=∠1+∠2=2x°=36°.
18.(1)1 3
(2)1 6
(3)1 n(n-1) 2n(n-1)
5.1 相交线
5.1.1 相交线
要点感知1 有一条公共边,另一边__________,具有这种位置关系的两个角互为邻补角.
预习练习1-1 如图,直线AB和CD相交于点O,则∠AOC的邻补角是__________.
1-2 如图,点A,O,B在同一直线上,已知∠BOC=50°,则∠AOC=__________.
要点感知2 有一个公共顶点,并且一个角的两边分别是另一个角的两边的__________,具有这种位置关系的两个角互为对顶角.
预习练习2-1 如图,直线AB和CD相交于点O,则∠AOC的对顶角是__________.
要点感知3 对顶角__________.
预习练习3-1 (2014·泉州)如图,直线AB与CD相交于点O,∠AOD=50°,则∠BOC=__________.
知识点1 认识对顶角和邻补角
1.(2014·凉山)下列图形中,∠1与∠2是对顶角的是( )
2.下列说法中,正确的是( )
A.相等的两个角是对顶角
B.有一条公共边的两个角是邻补角
C.有公共顶点的两个角是对顶角
D.一条直线与端点在这条直线上的一条射线组成的两个角是邻补角
3.如图所示,AB与CD相交所成的四个角中,∠1的邻补角是__________,∠1的对顶角是__________.
知识点2 邻补角和对顶角的性质
4.下面四个图形中,∠1=∠2一定成立的是( )
5.如图是一把剪刀,其中∠1=40°,则∠2=__________,其理由是____________________.
6.在括号内填写依据:
如图,因为直线a,b相交于点O,
所以∠1+∠3=180°(____________________),
∠1=∠2(____________________).
7.如图,O是直线AB上一点,∠COB=30°,则∠1=__________.
8.如图所示,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD=__________.
9.如图所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( )
A.62° B.118° C.72° D.59°
10.如图,三条直线l1,l2,l3相交于一点,则∠1+∠2+∠3等于( )
A.90° B.120° C.180° D.360°
11.(2013·大连)如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
12.如图,若∠1+∠3=180°,则图中与∠1相等的角有__________个,与∠1互补的角有__________个.
13.如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4=__________.
14.如图所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD-∠DOB=60°,则∠EOB=__________.
15.如图所示,AB,CD,EF交于点O,∠1=20°,∠2=60°,求∠BOC的度数.
16.如图所示,直线AB与CD相交于点O,OE平分∠AOD,∠BOC=80°,求∠BOD和∠AOE的度数.
17.如图所示,l1,l2,l3交于点O,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.
挑战自我
18.探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
参考答案
课前预习
要点感知1 互为反向延长线
预习练习1-1 ∠AOD和∠BOC
1-2 130°
要点感知2 反向延长线
预习练习2-1 ∠BOD
要点感知3 相等
预习练习3-1 50°
当堂训练
1.C 2.D 3.∠2,∠4∠3
4.B 5.40° 对顶角相等 6.邻补角互补 对顶角相等 7.150° 8.35°
课后作业
9.A 10.C 11.C 12.34 13.140° 14.150°
15.因为∠BOF=∠2=60°,
所以∠BOC=∠1+∠BOF=20°+60°=80°.
16.因为∠BOD与∠BOC是邻补角,∠BOC=80°,
所以∠BOD=180°—∠BOC=100°.
又因为∠AOD与∠BOC是对顶角,
所以∠AOD=∠BOC=80°.
又因为OE平分∠AOD,
所以∠AOE=∠BOC=40°.
17.设∠1=∠2=x°,则∠3=8x°.
由∠1+∠2+∠3=180°,得
10x=180.解得x=18.
所以∠1=∠2=18°.
所以∠4=∠1+∠2=2x°=36°.
18.(1)1 3
(2)1 6
(3)1 n(n-1) 2n(n-1)
