5.2.2 平行线的判定 课时练习
图片预览

文档简介
5.2.2 平行线的判定
要点感知 平行线的判定方法有:
(1)定义:在同一平面内,两条__________的直线互相平行;
(2)两条直线都与第三条直线__________,那么这两条直线也互相平行;
(3)同位角相等,两直线__________;
(4)内错角__________,两直线平行;
(5)__________互补,两直线平行;
(6)同一平面内,垂直于同一直线的两条直线互相__________.
预习练习1-1 如图,∠1=60°,∠2=60°,则直线a与b的位置关系是__________.
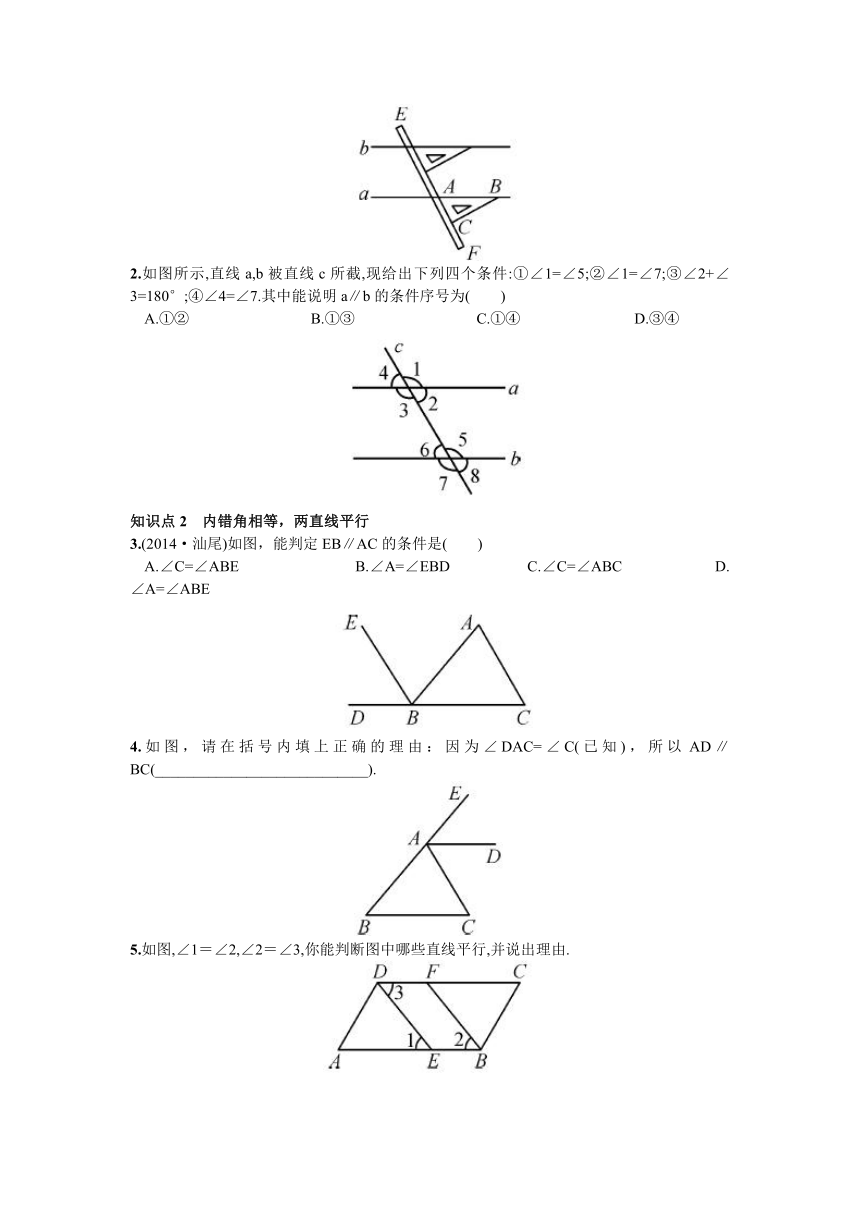
1-2 如图所示,直线AB,CD被直线EF所截,若∠1=_____,则AB∥CD;若∠3=_____,则AB∥CD;若∠2+_____=180°,则AB∥CD.
1-3 (2014·汕尾)已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是__________.
知识点1 同位角相等,两直线平行
1.(2014·滨州)如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,内错角相等
2.如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件序号为( )
A.①② B.①③ C.①④ D.③④
知识点2 内错角相等,两直线平行
3.(2014·汕尾)如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABE
4.如图,请在括号内填上正确的理由:因为∠DAC=∠C(已知),所以AD∥BC(____________________________).
5.如图,∠1=∠2,∠2=∠3,你能判断图中哪些直线平行,并说出理由.
知识点3 同旁内角互补,两直线平行
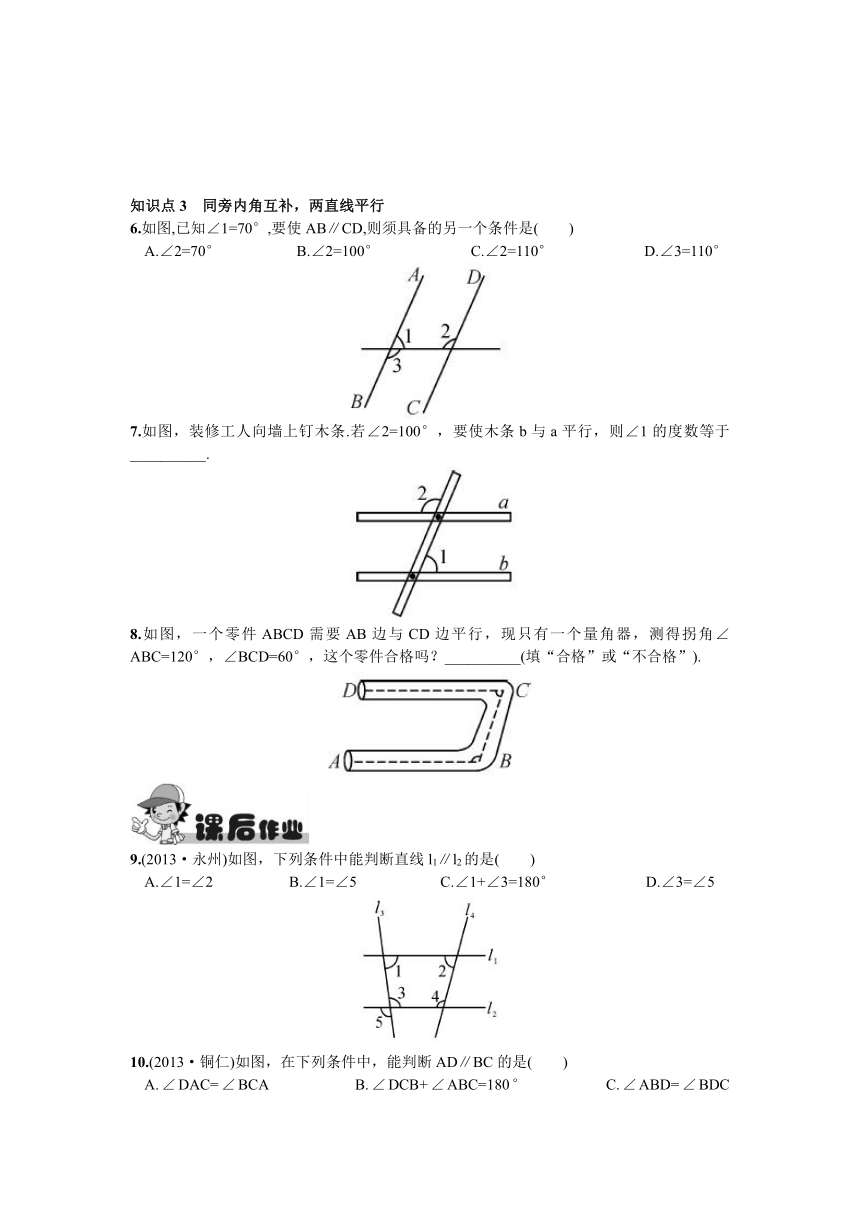
6.如图,已知∠1=70°,要使AB∥CD,则须具备的另一个条件是( )
A.∠2=70° B.∠2=100° C.∠2=110° D.∠3=110°
7.如图,装修工人向墙上钉木条.若∠2=100°,要使木条b与a平行,则∠1的度数等于__________.
8.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗?__________(填“合格”或“不合格”).
9.(2013·永州)如图,下列条件中能判断直线l1∥l2的是( )
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
10.(2013·铜仁)如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180° C.∠ABD=∠BDC D.∠BAC=∠ACD
11.对于图中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=180°
12.如图,直线a、b被直线c所截,若满足____________________,则a、b平行.
13.如图,用式子表示下列句子.
(1)因为∠1和∠B相等,根据“同位角相等,两直线平行”,所以DE和BC平行;
(2)因为∠1和∠2相等,根据“内错角相等,两直线平行”,所以AB和EF平行;
(3)因为∠BDE和∠B互补,根据“同旁内角互补,两直线平行”,所以DE和BC平行.
14.如图所示,推理填空:
(1)∵∠1=__________(已知),
∴AC∥ED(同位角相等,两直线平行).
(2)∵∠2=__________(已知),
∴AB∥FD(内错角相等,两直线平行).
(3)∵∠2+__________=180°(已知),
∴AC∥ED(同旁内角互补,两直线平行).
15.(2013·厦门)如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD.
16.如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由.
挑战自我
17.如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
参考答案
课前预习
要点感知 (1)不相交 (2)平行 (3)平行 (4)相等 (5)同旁内角 (6)平行
预习练习1-1 平行
1-2 ∠2 ∠2 ∠4
1-3 平行
当堂训练
1.A 2.A 3.D 4.内错角相等,两直线平行
5.DE∥BF,AB∥CD.
理由如下:
∵∠1=∠2,
∴DE∥BF(同位角相等,两直线平行).
∵∠2=∠3,
∴∠1=∠3(等量代换).
∴AB∥CD(内错角相等,两直线平行).
6.C 7.80° 8.合格
课后作业
9.C 10.A 11.D
12.答案不唯一,如:∠1=∠2或∠2=∠3或∠3+∠4=180°
13.(1)∵∠1=∠B(已知),
∴DE∥BC(同位角相等,两直线平行).
(2)∵∠1=∠2(已知),
∴EF∥AB(内错角相等,两直线平行).
(3)∵∠BDE+∠B=180°(已知),
∴DE∥BC(同旁内角互补,两直线平行).
14.(1)∠C
(2)∠BED
(3)∠AFD
15.∵∠ACD=70°,∠ACB=60°,
∴∠BCD=130°.
∵∠ABC=50°,
∴∠BCD+∠ABC=180°.
∴AB∥CD.
16.PG∥QH,AB∥CD.
∵PG平分∠APQ,QH平分∠DQP,
∴∠1=∠GPQ=∠APQ,∠PQH=∠2=∠PQD.
又∵∠1=∠2,
∴∠GPQ=∠PQH,∠APQ=∠PQD.
∴PG∥QH,AB∥CD.
17.CD∥EF.
理由如下:
∵AB⊥BD,CD⊥BD,
∴AB∥CD.
∵∠1+∠2=180°,
∴AB∥EF.
∴CD∥EF.
要点感知 平行线的判定方法有:
(1)定义:在同一平面内,两条__________的直线互相平行;
(2)两条直线都与第三条直线__________,那么这两条直线也互相平行;
(3)同位角相等,两直线__________;
(4)内错角__________,两直线平行;
(5)__________互补,两直线平行;
(6)同一平面内,垂直于同一直线的两条直线互相__________.
预习练习1-1 如图,∠1=60°,∠2=60°,则直线a与b的位置关系是__________.
1-2 如图所示,直线AB,CD被直线EF所截,若∠1=_____,则AB∥CD;若∠3=_____,则AB∥CD;若∠2+_____=180°,则AB∥CD.
1-3 (2014·汕尾)已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是__________.
知识点1 同位角相等,两直线平行
1.(2014·滨州)如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,内错角相等
2.如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件序号为( )
A.①② B.①③ C.①④ D.③④
知识点2 内错角相等,两直线平行
3.(2014·汕尾)如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABE
4.如图,请在括号内填上正确的理由:因为∠DAC=∠C(已知),所以AD∥BC(____________________________).
5.如图,∠1=∠2,∠2=∠3,你能判断图中哪些直线平行,并说出理由.
知识点3 同旁内角互补,两直线平行
6.如图,已知∠1=70°,要使AB∥CD,则须具备的另一个条件是( )
A.∠2=70° B.∠2=100° C.∠2=110° D.∠3=110°
7.如图,装修工人向墙上钉木条.若∠2=100°,要使木条b与a平行,则∠1的度数等于__________.
8.如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗?__________(填“合格”或“不合格”).
9.(2013·永州)如图,下列条件中能判断直线l1∥l2的是( )
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
10.(2013·铜仁)如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180° C.∠ABD=∠BDC D.∠BAC=∠ACD
11.对于图中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=180°
12.如图,直线a、b被直线c所截,若满足____________________,则a、b平行.
13.如图,用式子表示下列句子.
(1)因为∠1和∠B相等,根据“同位角相等,两直线平行”,所以DE和BC平行;
(2)因为∠1和∠2相等,根据“内错角相等,两直线平行”,所以AB和EF平行;
(3)因为∠BDE和∠B互补,根据“同旁内角互补,两直线平行”,所以DE和BC平行.
14.如图所示,推理填空:
(1)∵∠1=__________(已知),
∴AC∥ED(同位角相等,两直线平行).
(2)∵∠2=__________(已知),
∴AB∥FD(内错角相等,两直线平行).
(3)∵∠2+__________=180°(已知),
∴AC∥ED(同旁内角互补,两直线平行).
15.(2013·厦门)如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.试说明:AB∥CD.
16.如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由.
挑战自我
17.如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
参考答案
课前预习
要点感知 (1)不相交 (2)平行 (3)平行 (4)相等 (5)同旁内角 (6)平行
预习练习1-1 平行
1-2 ∠2 ∠2 ∠4
1-3 平行
当堂训练
1.A 2.A 3.D 4.内错角相等,两直线平行
5.DE∥BF,AB∥CD.
理由如下:
∵∠1=∠2,
∴DE∥BF(同位角相等,两直线平行).
∵∠2=∠3,
∴∠1=∠3(等量代换).
∴AB∥CD(内错角相等,两直线平行).
6.C 7.80° 8.合格
课后作业
9.C 10.A 11.D
12.答案不唯一,如:∠1=∠2或∠2=∠3或∠3+∠4=180°
13.(1)∵∠1=∠B(已知),
∴DE∥BC(同位角相等,两直线平行).
(2)∵∠1=∠2(已知),
∴EF∥AB(内错角相等,两直线平行).
(3)∵∠BDE+∠B=180°(已知),
∴DE∥BC(同旁内角互补,两直线平行).
14.(1)∠C
(2)∠BED
(3)∠AFD
15.∵∠ACD=70°,∠ACB=60°,
∴∠BCD=130°.
∵∠ABC=50°,
∴∠BCD+∠ABC=180°.
∴AB∥CD.
16.PG∥QH,AB∥CD.
∵PG平分∠APQ,QH平分∠DQP,
∴∠1=∠GPQ=∠APQ,∠PQH=∠2=∠PQD.
又∵∠1=∠2,
∴∠GPQ=∠PQH,∠APQ=∠PQD.
∴PG∥QH,AB∥CD.
17.CD∥EF.
理由如下:
∵AB⊥BD,CD⊥BD,
∴AB∥CD.
∵∠1+∠2=180°,
∴AB∥EF.
∴CD∥EF.
