5.3.1 平行线的性质第1课时 平行线的性质 课时练习
文档属性
| 名称 | 5.3.1 平行线的性质第1课时 平行线的性质 课时练习 |  | |
| 格式 | doc | ||
| 文件大小 | 150.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 10:48:33 | ||
图片预览

文档简介
5.3 平行线的性质
5.3.1 平行线的性质
第1课时 平行线的性质
要点感知 平行线的性质:
性质1:两直线平行,同位角__________;
性质2:两直线__________,内错角相等;
性质3:两直线平行,__________互补.
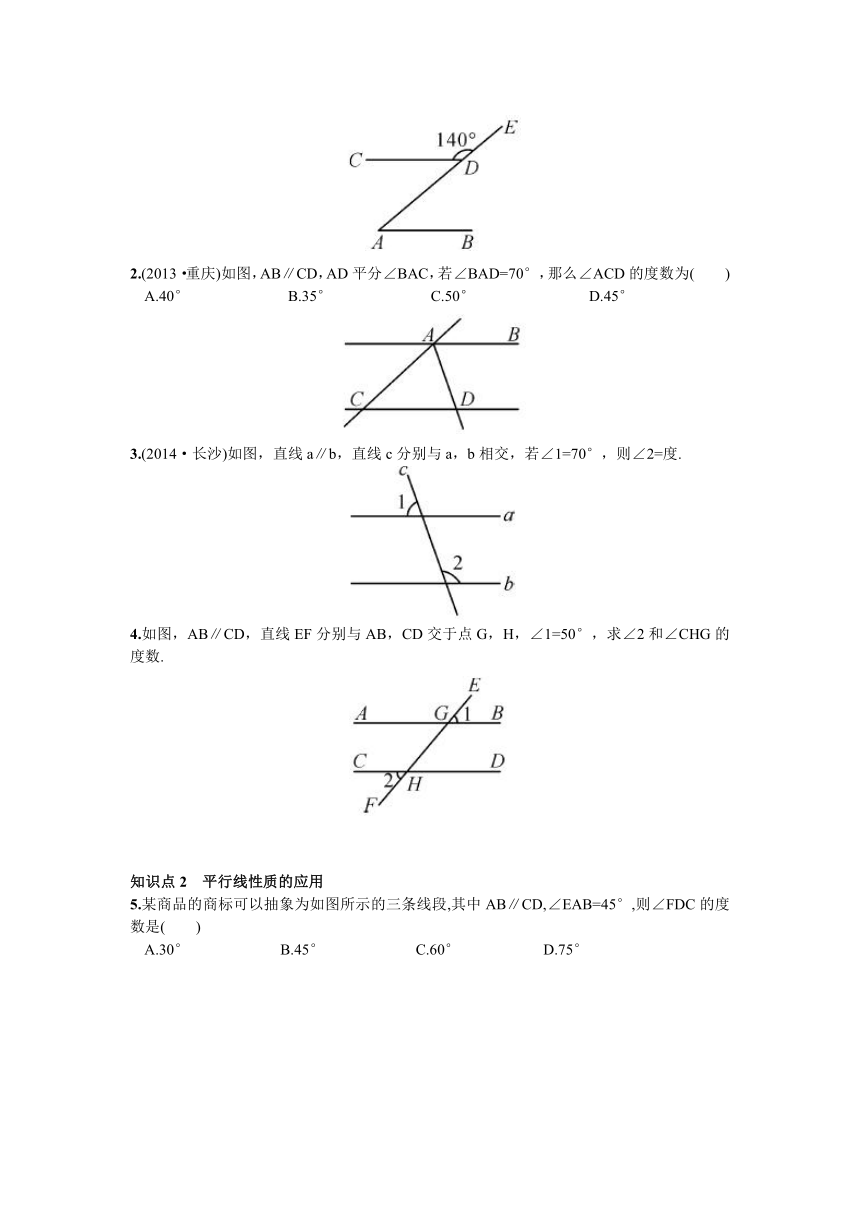
预习练习1-1 (2014·宜宾)如图,直线a、b被第三条直线c所截,如果a∥b,∠1=70°,那么∠3的度数是__________.
1-2 如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东__________.
1-3 如图,AB∥CD,∠1=85°,则∠2=__________.
知识点1 平行线的性质
1.(2013·枣庄)如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
A.140° B.60° C.50° D.40°
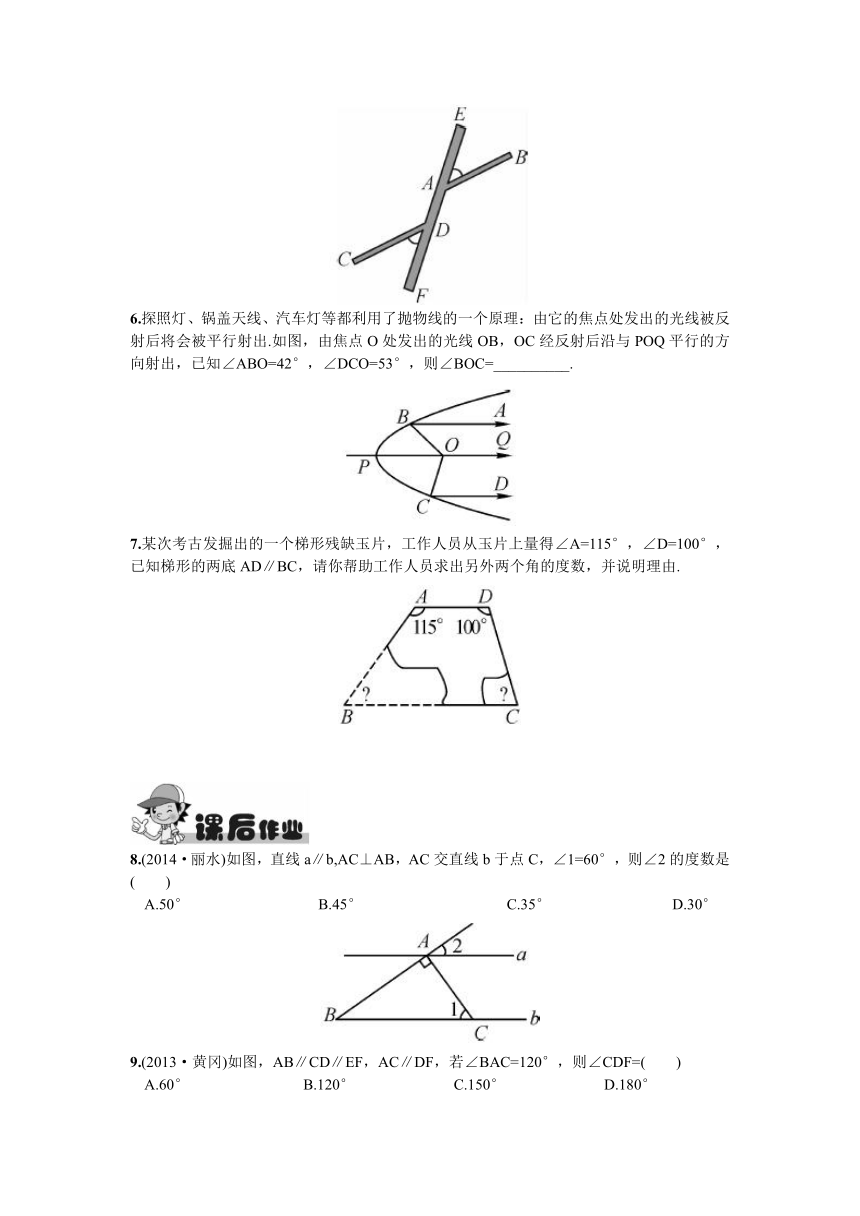
2.(2013·重庆)如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为( )
A.40° B.35° C.50° D.45°
3.(2014·长沙)如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2=度.
4.如图,AB∥CD,直线EF分别与AB,CD交于点G,H,∠1=50°,求∠2和∠CHG的度数.
知识点2 平行线性质的应用
5.某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是( )
A.30° B.45° C.60° D.75°
6.探照灯、锅盖天线、汽车灯等都利用了抛物线的一个原理:由它的焦点处发出的光线被反射后将会被平行射出.如图,由焦点O处发出的光线OB,OC经反射后沿与POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,则∠BOC=__________.
7.某次考古发掘出的一个梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.
8.(2014·丽水)如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=60°,则∠2的度数是( )
A.50° B.45° C.35° D.30°
9.(2013·黄冈)如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=( )
A.60° B.120° C.150° D.180°
10.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
11.(2013·成都)如图,∠B=30°,若AB∥CD,CB平分∠ACD,则∠ACD=__________.
12.如图,点B、C、D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A=__________.
13.(2014·益阳)如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
14.如图,已知AB∥CD,∠B=40°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.
15.如图:已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
挑战自我
16.如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).
参考答案
课前预习
要点感知 相等 平行 同旁内角
预习练习1-1 70°
1-2 42°
1-3 95°
当堂训练
1.D 2.A 3.110
4.∵AB∥CD,
∴∠DHE=∠1=50°.
∵∠2=∠DHE,
∴∠2=∠1=50°.
∵∠2+∠CHG=180°,
∴∠CHG=180°-∠2=130°.
5.B 6.95°
7.∵AD∥BC,∠A=115°,∠D=100°,
∴∠B=180°-∠A=180°-115°=65°,∠C=180°-∠D=180°-100°=80°.
课后作业
8.D 9.A 10.D 11.60° 12.54°
13.∵EF∥BC,
∴∠BAF=180°-∠B=100°.
∵AC平分∠BAF,
∴∠CAF=∠BAF=50°.
∵EF∥BC,
∴∠C=∠CAF=50°.
14.∵AB∥CD,
∴∠BCE+∠B=180°.
∵∠B=40°,
∴∠BCE=180°-40°=140°.
∵CN是∠BCE的平分线,
∴∠BCN=∠BCE=×140°=70°.
∵CM⊥CN,
∴∠BCM=90°-70°=20°.
15.∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°.
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°.
∴∠DCF=50°.
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
16.(1)∠1+∠2=∠3.
理由:过点P作l1的平行线PQ.
∵l1∥l2,
∴l1∥l2∥PQ.
∴∠1=∠4,∠2=∠5.
∵∠4+∠5=∠3,
∴∠1+∠2=∠3.
(2)∠1+∠2=∠3不变.
(3)∠1-∠2=∠3或∠2-∠1=∠3.
理由:①当点P在下侧时,如图,过点P作l1的平行线PQ.
∵l1∥l2,
∴l1∥l2∥PQ.
∴∠2=∠4,∠1=∠3+∠4.
∴∠1-∠2=∠3.
②当点P在上侧时,同理可得∠2-∠1=∠3.
5.3.1 平行线的性质
第1课时 平行线的性质
要点感知 平行线的性质:
性质1:两直线平行,同位角__________;
性质2:两直线__________,内错角相等;
性质3:两直线平行,__________互补.
预习练习1-1 (2014·宜宾)如图,直线a、b被第三条直线c所截,如果a∥b,∠1=70°,那么∠3的度数是__________.
1-2 如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东__________.
1-3 如图,AB∥CD,∠1=85°,则∠2=__________.
知识点1 平行线的性质
1.(2013·枣庄)如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
A.140° B.60° C.50° D.40°
2.(2013·重庆)如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为( )
A.40° B.35° C.50° D.45°
3.(2014·长沙)如图,直线a∥b,直线c分别与a,b相交,若∠1=70°,则∠2=度.
4.如图,AB∥CD,直线EF分别与AB,CD交于点G,H,∠1=50°,求∠2和∠CHG的度数.
知识点2 平行线性质的应用
5.某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是( )
A.30° B.45° C.60° D.75°
6.探照灯、锅盖天线、汽车灯等都利用了抛物线的一个原理:由它的焦点处发出的光线被反射后将会被平行射出.如图,由焦点O处发出的光线OB,OC经反射后沿与POQ平行的方向射出,已知∠ABO=42°,∠DCO=53°,则∠BOC=__________.
7.某次考古发掘出的一个梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°,已知梯形的两底AD∥BC,请你帮助工作人员求出另外两个角的度数,并说明理由.
8.(2014·丽水)如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=60°,则∠2的度数是( )
A.50° B.45° C.35° D.30°
9.(2013·黄冈)如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=( )
A.60° B.120° C.150° D.180°
10.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
11.(2013·成都)如图,∠B=30°,若AB∥CD,CB平分∠ACD,则∠ACD=__________.
12.如图,点B、C、D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A=__________.
13.(2014·益阳)如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
14.如图,已知AB∥CD,∠B=40°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.
15.如图:已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
挑战自我
16.如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).
参考答案
课前预习
要点感知 相等 平行 同旁内角
预习练习1-1 70°
1-2 42°
1-3 95°
当堂训练
1.D 2.A 3.110
4.∵AB∥CD,
∴∠DHE=∠1=50°.
∵∠2=∠DHE,
∴∠2=∠1=50°.
∵∠2+∠CHG=180°,
∴∠CHG=180°-∠2=130°.
5.B 6.95°
7.∵AD∥BC,∠A=115°,∠D=100°,
∴∠B=180°-∠A=180°-115°=65°,∠C=180°-∠D=180°-100°=80°.
课后作业
8.D 9.A 10.D 11.60° 12.54°
13.∵EF∥BC,
∴∠BAF=180°-∠B=100°.
∵AC平分∠BAF,
∴∠CAF=∠BAF=50°.
∵EF∥BC,
∴∠C=∠CAF=50°.
14.∵AB∥CD,
∴∠BCE+∠B=180°.
∵∠B=40°,
∴∠BCE=180°-40°=140°.
∵CN是∠BCE的平分线,
∴∠BCN=∠BCE=×140°=70°.
∵CM⊥CN,
∴∠BCM=90°-70°=20°.
15.∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°.
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°.
∴∠DCF=50°.
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
16.(1)∠1+∠2=∠3.
理由:过点P作l1的平行线PQ.
∵l1∥l2,
∴l1∥l2∥PQ.
∴∠1=∠4,∠2=∠5.
∵∠4+∠5=∠3,
∴∠1+∠2=∠3.
(2)∠1+∠2=∠3不变.
(3)∠1-∠2=∠3或∠2-∠1=∠3.
理由:①当点P在下侧时,如图,过点P作l1的平行线PQ.
∵l1∥l2,
∴l1∥l2∥PQ.
∴∠2=∠4,∠1=∠3+∠4.
∴∠1-∠2=∠3.
②当点P在上侧时,同理可得∠2-∠1=∠3.
