5.3.1 平行线的性质第2课时 平行线的性质与判定的综合运用 课时练习
文档属性
| 名称 | 5.3.1 平行线的性质第2课时 平行线的性质与判定的综合运用 课时练习 |
|
|
| 格式 | doc | ||
| 文件大小 | 166.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 00:00:00 | ||
图片预览

文档简介
第2课时 平行线的性质与判定的综合运用
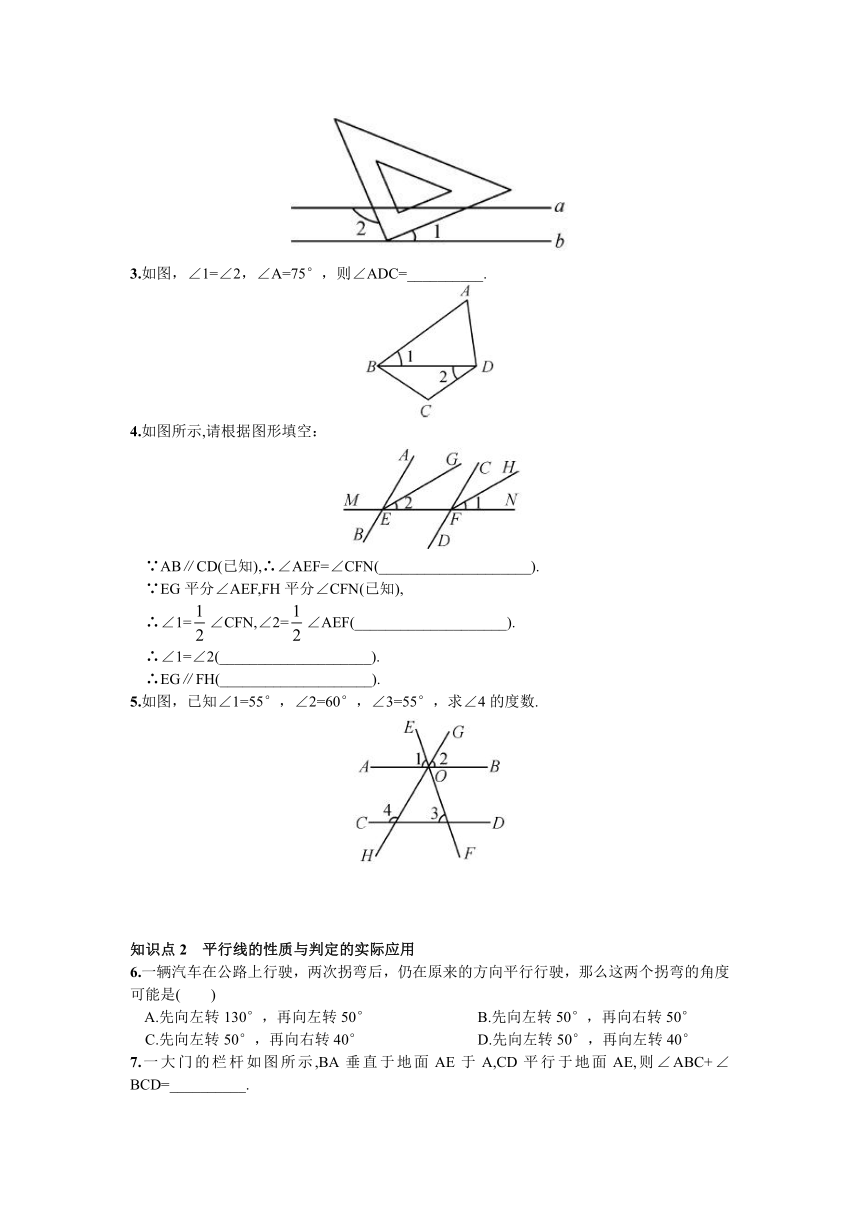
预习练习1-1 如图所示,把下面的推理补充完整:
①∵∠1+∠α=180°,∴__________(____________________).
②∵∠1=∠γ,∴__________(____________________).
③∵∠β=∠γ,∴__________(____________________).
④∵l1∥l2,l3∥l2,∴__________(____________________).
1-2 (2013·随州)如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A.35° B.70° C.90° D.110°
知识点1 平行线的性质与判定的综合运用
1.如图,直线AB、CD相交于点O,OT⊥AB于点O,CE∥AB交CD于点C,若∠ECO=30°,则∠DOT=( )
A.30° B.45° C.60° D.120°
2.(2014·仙桃)如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( )
A.100° B.110° C.120° D.130°
3.如图,∠1=∠2,∠A=75°,则∠ADC=__________.
4.如图所示,请根据图形填空:
∵AB∥CD(已知),∴∠AEF=∠CFN(____________________).
∵EG平分∠AEF,FH平分∠CFN(已知),
∴∠1=∠CFN,∠2=∠AEF(____________________).
∴∠1=∠2(____________________).
∴EG∥FH(____________________).
5.如图,已知∠1=55°,∠2=60°,∠3=55°,求∠4的度数.
知识点2 平行线的性质与判定的实际应用
6.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )
A.先向左转130°,再向左转50° B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40° D.先向左转50°,再向左转40°
7.一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=__________.
8.如图,一只船从点A出发沿北偏东60°方向航行到点B,再以南偏西25°方向返回,则∠ABC=__________.
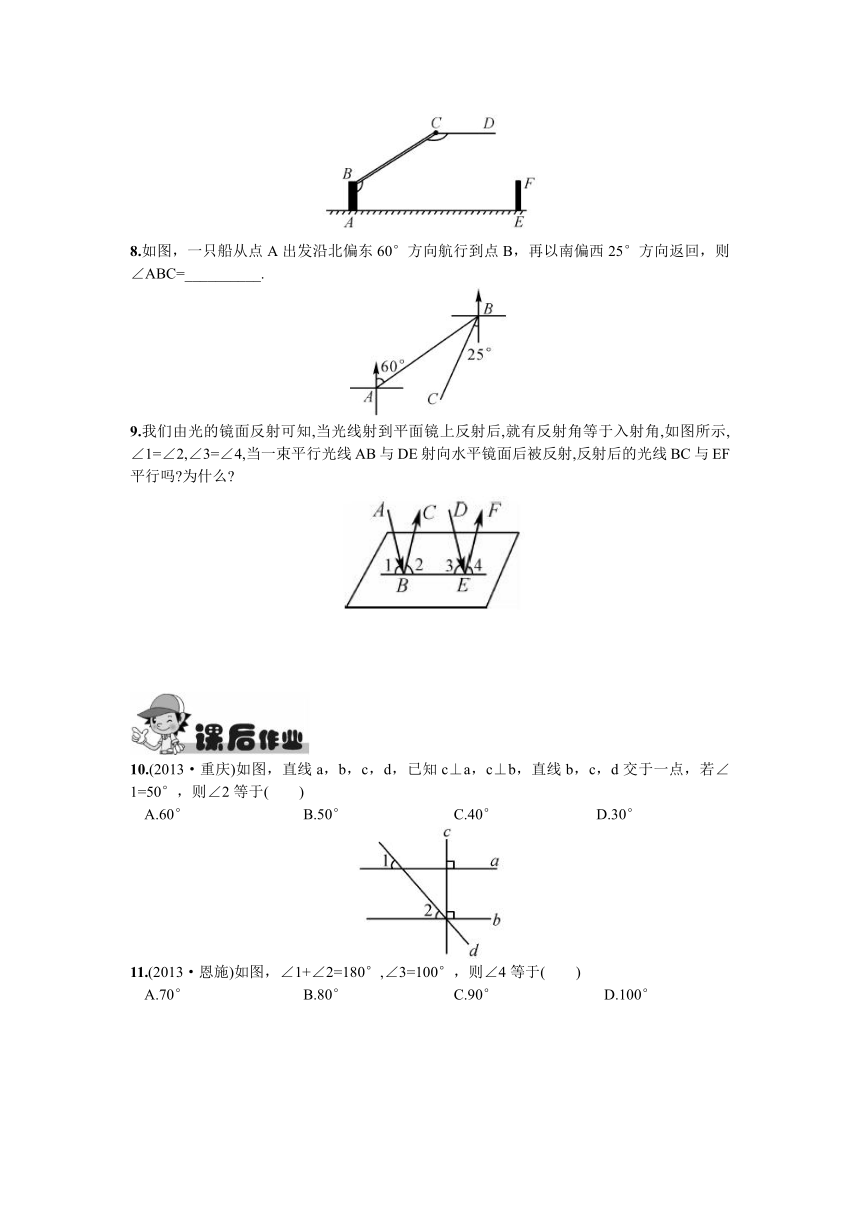
9.我们由光的镜面反射可知,当光线射到平面镜上反射后,就有反射角等于入射角,如图所示,∠1=∠2,∠3=∠4,当一束平行光线AB与DE射向水平镜面后被反射,反射后的光线BC与EF平行吗 为什么
10.(2013·重庆)如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2等于( )
A.60° B.50° C.40° D.30°
11.(2013·恩施)如图,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
12.(2013·孝感)如图,∠1=∠2,∠3=40°.则∠4等于( )
A.120° B.130° C.140° D.40°
13.(2014·龙岩)如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
A.40° B.50° C.70° D.80°
14.如图所示,AB∥CD,∠E=37°,∠C=20°,∠EAB的度数为( )
A.57° B.60° C.63° D.123°
15.(2013·广安)如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=__________.
16.如图,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
17.如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3.请问:AD平分∠BAC吗?若平分,请说明理由.
18.如图,E为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,试说明AC∥DF,并在每步后面批注依据.
挑战自我
19.探究题:
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?
参考答案
课前预习
预习练习1-1 ①l1∥l2 同旁内角互补,两直线平行
②l3∥l2 同位角相等,两直线平行
③l3∥l2 内错角相等,两直线平行
④l1∥l3 平行于同一条直线的两条直线平行
1-2 D
当堂训练
1.C 2.D 3.105°
4.两直线平行,同位角相等 角平分线定义 等量代换 同位角相等,两直线平行
5.∵∠1=∠3,
∴AB∥CD.
∴∠AOG=∠4.
∵∠2=60°,
∴∠AOG=180°-∠2=120°.
∴∠4=120°.
6.B 7.270° 8.35°
9.BC∥EF.
理由如下:
∵AB∥DE,
∴∠1=∠3(两直线平行,同位角相等).
又∵∠1=∠2,∠3=∠4,
∴∠2=∠4.
∴BC∥EF(同位角相等,两直线平行).
课后作业
10.B 11.D 12.C 13.C 14.A 15.63°30′
16.∵∠1=72°,∠2=72°,
∴∠1=∠2.
∴a∥b.
∴∠3+∠4=180°.
∵∠3=60°,
∴∠4=120°.
17.AD平分∠BAC.
理由:∵AD⊥BC,EG⊥BC,
∴∠ADC=∠EGC=90°.
∴AD∥EG.
∴∠3=∠2,∠E=∠1.
∵∠3=∠E,
∴∠1=∠2,即AD平分∠BAC.
18.∵∠1=∠2(已知),∠4=∠2(对顶角相等),
∴∠4=∠1(等量代换).
∴DB∥CE(同位角相等,两直线平行).
∴∠C=∠ABD(两直线平行,同位角相等).
∵∠C=∠D(已知),
∴∠D=∠ABD(等量代换).
∴AC∥DF(内错角相等,两直线平行).
19.(1)理由:过点E作EF∥AB,
∴∠B=∠BEF.
∵CD∥AB,
∴CD∥EF.
∴∠D=∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠BED.
(2)AB∥CD.
(3)∠B+∠D+∠E=360°.
(4)∠B=∠D+∠E.
(5)∠E+∠G=∠B+∠F+∠D.
预习练习1-1 如图所示,把下面的推理补充完整:
①∵∠1+∠α=180°,∴__________(____________________).
②∵∠1=∠γ,∴__________(____________________).
③∵∠β=∠γ,∴__________(____________________).
④∵l1∥l2,l3∥l2,∴__________(____________________).
1-2 (2013·随州)如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A.35° B.70° C.90° D.110°
知识点1 平行线的性质与判定的综合运用
1.如图,直线AB、CD相交于点O,OT⊥AB于点O,CE∥AB交CD于点C,若∠ECO=30°,则∠DOT=( )
A.30° B.45° C.60° D.120°
2.(2014·仙桃)如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( )
A.100° B.110° C.120° D.130°
3.如图,∠1=∠2,∠A=75°,则∠ADC=__________.
4.如图所示,请根据图形填空:
∵AB∥CD(已知),∴∠AEF=∠CFN(____________________).
∵EG平分∠AEF,FH平分∠CFN(已知),
∴∠1=∠CFN,∠2=∠AEF(____________________).
∴∠1=∠2(____________________).
∴EG∥FH(____________________).
5.如图,已知∠1=55°,∠2=60°,∠3=55°,求∠4的度数.
知识点2 平行线的性质与判定的实际应用
6.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )
A.先向左转130°,再向左转50° B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40° D.先向左转50°,再向左转40°
7.一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=__________.
8.如图,一只船从点A出发沿北偏东60°方向航行到点B,再以南偏西25°方向返回,则∠ABC=__________.
9.我们由光的镜面反射可知,当光线射到平面镜上反射后,就有反射角等于入射角,如图所示,∠1=∠2,∠3=∠4,当一束平行光线AB与DE射向水平镜面后被反射,反射后的光线BC与EF平行吗 为什么
10.(2013·重庆)如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2等于( )
A.60° B.50° C.40° D.30°
11.(2013·恩施)如图,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
12.(2013·孝感)如图,∠1=∠2,∠3=40°.则∠4等于( )
A.120° B.130° C.140° D.40°
13.(2014·龙岩)如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
A.40° B.50° C.70° D.80°
14.如图所示,AB∥CD,∠E=37°,∠C=20°,∠EAB的度数为( )
A.57° B.60° C.63° D.123°
15.(2013·广安)如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=__________.
16.如图,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
17.如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3.请问:AD平分∠BAC吗?若平分,请说明理由.
18.如图,E为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,试说明AC∥DF,并在每步后面批注依据.
挑战自我
19.探究题:
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?
参考答案
课前预习
预习练习1-1 ①l1∥l2 同旁内角互补,两直线平行
②l3∥l2 同位角相等,两直线平行
③l3∥l2 内错角相等,两直线平行
④l1∥l3 平行于同一条直线的两条直线平行
1-2 D
当堂训练
1.C 2.D 3.105°
4.两直线平行,同位角相等 角平分线定义 等量代换 同位角相等,两直线平行
5.∵∠1=∠3,
∴AB∥CD.
∴∠AOG=∠4.
∵∠2=60°,
∴∠AOG=180°-∠2=120°.
∴∠4=120°.
6.B 7.270° 8.35°
9.BC∥EF.
理由如下:
∵AB∥DE,
∴∠1=∠3(两直线平行,同位角相等).
又∵∠1=∠2,∠3=∠4,
∴∠2=∠4.
∴BC∥EF(同位角相等,两直线平行).
课后作业
10.B 11.D 12.C 13.C 14.A 15.63°30′
16.∵∠1=72°,∠2=72°,
∴∠1=∠2.
∴a∥b.
∴∠3+∠4=180°.
∵∠3=60°,
∴∠4=120°.
17.AD平分∠BAC.
理由:∵AD⊥BC,EG⊥BC,
∴∠ADC=∠EGC=90°.
∴AD∥EG.
∴∠3=∠2,∠E=∠1.
∵∠3=∠E,
∴∠1=∠2,即AD平分∠BAC.
18.∵∠1=∠2(已知),∠4=∠2(对顶角相等),
∴∠4=∠1(等量代换).
∴DB∥CE(同位角相等,两直线平行).
∴∠C=∠ABD(两直线平行,同位角相等).
∵∠C=∠D(已知),
∴∠D=∠ABD(等量代换).
∴AC∥DF(内错角相等,两直线平行).
19.(1)理由:过点E作EF∥AB,
∴∠B=∠BEF.
∵CD∥AB,
∴CD∥EF.
∴∠D=∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠BED.
(2)AB∥CD.
(3)∠B+∠D+∠E=360°.
(4)∠B=∠D+∠E.
(5)∠E+∠G=∠B+∠F+∠D.
