9.2 一元一次不等式第1课时 一元一次不等式的解法 课时练习
文档属性
| 名称 | 9.2 一元一次不等式第1课时 一元一次不等式的解法 课时练习 |  | |
| 格式 | doc | ||
| 文件大小 | 157.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 10:48:33 | ||
图片预览

文档简介
9.2 一元一次不等式
第1课时 一元一次不等式的解法
要点感知1 含有__________未知数,并且未知数的次数是__________的不等式,叫做一元一次不等式.
预习练习1-1 下列不等式中,属于一元一次不等式的是( )
A.4>1 B.3x-24<4 C.<2 D.4x-3<2y-7
要点感知2 解一元一次不等式,要依据__________,将不等式逐步化为__________的形式.
预习练习2-1 不等式-x>3的解集是( )
A.x>-3 B.x<-3 C.x<3 D.x>3
要点感知3 解一元一次不等式的一般步骤:
(1)去分母(根据不等式的__________);
(2)去括号(根据__________);
(3)移项(根据不等式的__________);
(4)合并(根据__________);
(5)系数化为1(根据不等式的__________).
预习练习3-1 解不等式2(x-1)-3<1,并把它的解集在数轴上表示出来.
知识点1 一元一次不等式及其解法
1.(2014·沈阳)一元一次不等式x-1≥0的解集在数轴上表示正确的是( )
2.(2013·桂林)不等式x+1>2x-4的解集是( )
A.x<5 B.x>5 C.x<1 D.x>1
3.不等式4-3x≥2x-6的非负整数解有( )
A.1个 B.2个 C.3个 D.4个
4.如果关于x的不等式(a+1)x>a+1的解集为x<1,那么a的取值范围是( )
A.a>0 B.a<0 C.a>-1 D.a<-1
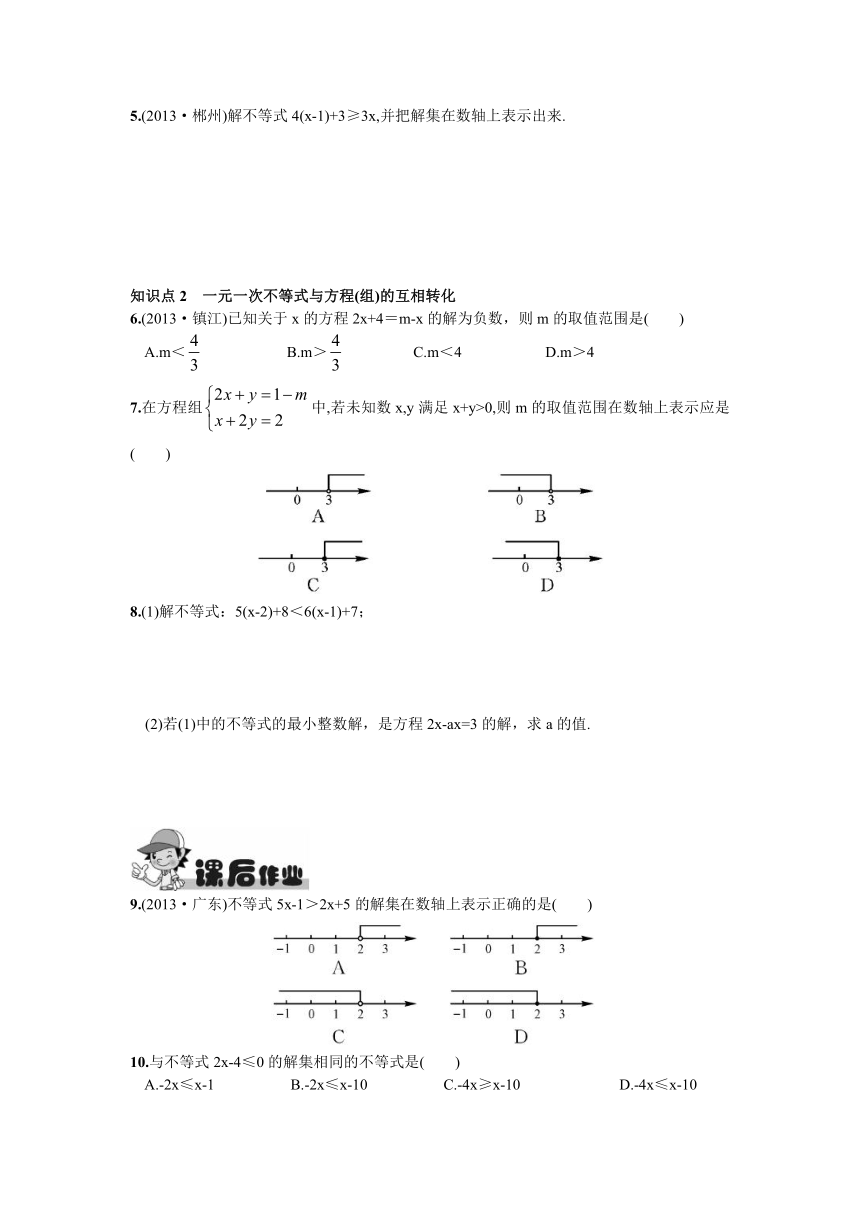
5.(2013·郴州)解不等式4(x-1)+3≥3x,并把解集在数轴上表示出来.
知识点2 一元一次不等式与方程(组)的互相转化
6.(2013·镇江)已知关于x的方程2x+4=m-x的解为负数,则m的取值范围是( )
A.m< B.m> C.m<4 D.m>4
7.在方程组中,若未知数x,y满足x+y>0,则m的取值范围在数轴上表示应是( )
8.(1)解不等式:5(x-2)+8<6(x-1)+7;
(2)若(1)中的不等式的最小整数解,是方程2x-ax=3的解,求a的值.
9.(2013·广东)不等式5x-1>2x+5的解集在数轴上表示正确的是( )
10.与不等式2x-4≤0的解集相同的不等式是( )
A.-2x≤x-1 B.-2x≤x-10 C.-4x≥x-10 D.-4x≤x-10
11.不等式2x-3<的解集是__________.
12.(2013·张掖)不等式2x+9≥3(x+2)的正整数解是__________.
13.(2013·荆州)在实数范围内规定新运算“△”,其规则是:a△b=2a-b.已知不等式x△k≥1的解集在数轴上如图表示,则k的值是__________.
14.如果a<2,那么不等式ax>2x+5的解集是__________.
15.解下列不等式,并把解集在数轴上表示出来.
(1)(2012·连云港)x-1>2x;
(2)-x>1;
(3)(2013·巴中)-≤1.
16.下面解不等式的过程是否正确,如不正确,请找出,并改正.
解不等式:-1<.
解:去分母,得2(4-2x)-1<3(6-4x).①
去括号,得8-4x-1<18-12x.②
移项,合并,得8x<11.③
系数化为1,得x<.④
挑战自我
17.已知关于x的方程4(x+2)-2=5+3a的解不小于方程=的解,试求a的取值范围.
参考答案
课前预习
要点感知1 一个 1
预习练习1-1 B
要点感知2 不等式的性质 xa
预习练习2-1 B
要点感知3 (1)性质2 (2)去括号法则 (3)性质1 (4)合并同类项的法则 (5)性质2或性质3
预习练习3-1 去括号,得2x-2-3<1.
移项,得2x<2+3+1.
系数化为1,得x<3.
不等式的解集在数轴上表示如图.
当堂训练
1.A 2.A 3.C 4.D
5.去括号,得4x-4+3≥3x.
移项,得4x-3x≥4-3.
合并,得x≥1.
故不等式的解集为:x≥1.
用数轴表示解集为:
6.C 7.B
8.(1)5x-10+8<6x-6+7.
5x-6x<-6+7+10-8.
-x<3.
所以x>-3.
(2)由(1)得,x的最小整数解为-2,故2×(-2)-a×(-2)=3.解得a=.
课后作业
9.A 10.C 11.x<2 12.1,2,3 13.-3 14.x<
15.(1)移项,得x-2x>1.
合并,得-x>1.
系数化为1,得x<-2.
其解集在数轴上表示为:
(2)去分母,得5x-1-3x>3.
移项,得2x>4.
系数化为1,得x>2.
把不等式的解集在数轴上表示为:
(3)去分母,得2(2x-1)-(9x+2)≤6.
去括号,得4x-2-9x-2≤6.
移项,得4x-9x≤6+2+2.
合并同类项,得-5x≤10.
系数化为1,得x≥-2.
把不等式的解集在数轴上表示为:
16.①不正确.
去分母,得2(4-2x)-6<3(6-4x).
去括号、移项、合并,得8x<16.
解得x<2.
17.解方程4(x+2)-2=5+3a,得x=.
解方程=,得x=.
依题意,得≥.解得a≤-.
故a的取值范围为a≤-.
第1课时 一元一次不等式的解法
要点感知1 含有__________未知数,并且未知数的次数是__________的不等式,叫做一元一次不等式.
预习练习1-1 下列不等式中,属于一元一次不等式的是( )
A.4>1 B.3x-24<4 C.<2 D.4x-3<2y-7
要点感知2 解一元一次不等式,要依据__________,将不等式逐步化为__________的形式.
预习练习2-1 不等式-x>3的解集是( )
A.x>-3 B.x<-3 C.x<3 D.x>3
要点感知3 解一元一次不等式的一般步骤:
(1)去分母(根据不等式的__________);
(2)去括号(根据__________);
(3)移项(根据不等式的__________);
(4)合并(根据__________);
(5)系数化为1(根据不等式的__________).
预习练习3-1 解不等式2(x-1)-3<1,并把它的解集在数轴上表示出来.
知识点1 一元一次不等式及其解法
1.(2014·沈阳)一元一次不等式x-1≥0的解集在数轴上表示正确的是( )
2.(2013·桂林)不等式x+1>2x-4的解集是( )
A.x<5 B.x>5 C.x<1 D.x>1
3.不等式4-3x≥2x-6的非负整数解有( )
A.1个 B.2个 C.3个 D.4个
4.如果关于x的不等式(a+1)x>a+1的解集为x<1,那么a的取值范围是( )
A.a>0 B.a<0 C.a>-1 D.a<-1
5.(2013·郴州)解不等式4(x-1)+3≥3x,并把解集在数轴上表示出来.
知识点2 一元一次不等式与方程(组)的互相转化
6.(2013·镇江)已知关于x的方程2x+4=m-x的解为负数,则m的取值范围是( )
A.m< B.m> C.m<4 D.m>4
7.在方程组中,若未知数x,y满足x+y>0,则m的取值范围在数轴上表示应是( )
8.(1)解不等式:5(x-2)+8<6(x-1)+7;
(2)若(1)中的不等式的最小整数解,是方程2x-ax=3的解,求a的值.
9.(2013·广东)不等式5x-1>2x+5的解集在数轴上表示正确的是( )
10.与不等式2x-4≤0的解集相同的不等式是( )
A.-2x≤x-1 B.-2x≤x-10 C.-4x≥x-10 D.-4x≤x-10
11.不等式2x-3<的解集是__________.
12.(2013·张掖)不等式2x+9≥3(x+2)的正整数解是__________.
13.(2013·荆州)在实数范围内规定新运算“△”,其规则是:a△b=2a-b.已知不等式x△k≥1的解集在数轴上如图表示,则k的值是__________.
14.如果a<2,那么不等式ax>2x+5的解集是__________.
15.解下列不等式,并把解集在数轴上表示出来.
(1)(2012·连云港)x-1>2x;
(2)-x>1;
(3)(2013·巴中)-≤1.
16.下面解不等式的过程是否正确,如不正确,请找出,并改正.
解不等式:-1<.
解:去分母,得2(4-2x)-1<3(6-4x).①
去括号,得8-4x-1<18-12x.②
移项,合并,得8x<11.③
系数化为1,得x<.④
挑战自我
17.已知关于x的方程4(x+2)-2=5+3a的解不小于方程=的解,试求a的取值范围.
参考答案
课前预习
要点感知1 一个 1
预习练习1-1 B
要点感知2 不等式的性质 x
预习练习2-1 B
要点感知3 (1)性质2 (2)去括号法则 (3)性质1 (4)合并同类项的法则 (5)性质2或性质3
预习练习3-1 去括号,得2x-2-3<1.
移项,得2x<2+3+1.
系数化为1,得x<3.
不等式的解集在数轴上表示如图.
当堂训练
1.A 2.A 3.C 4.D
5.去括号,得4x-4+3≥3x.
移项,得4x-3x≥4-3.
合并,得x≥1.
故不等式的解集为:x≥1.
用数轴表示解集为:
6.C 7.B
8.(1)5x-10+8<6x-6+7.
5x-6x<-6+7+10-8.
-x<3.
所以x>-3.
(2)由(1)得,x的最小整数解为-2,故2×(-2)-a×(-2)=3.解得a=.
课后作业
9.A 10.C 11.x<2 12.1,2,3 13.-3 14.x<
15.(1)移项,得x-2x>1.
合并,得-x>1.
系数化为1,得x<-2.
其解集在数轴上表示为:
(2)去分母,得5x-1-3x>3.
移项,得2x>4.
系数化为1,得x>2.
把不等式的解集在数轴上表示为:
(3)去分母,得2(2x-1)-(9x+2)≤6.
去括号,得4x-2-9x-2≤6.
移项,得4x-9x≤6+2+2.
合并同类项,得-5x≤10.
系数化为1,得x≥-2.
把不等式的解集在数轴上表示为:
16.①不正确.
去分母,得2(4-2x)-6<3(6-4x).
去括号、移项、合并,得8x<16.
解得x<2.
17.解方程4(x+2)-2=5+3a,得x=.
解方程=,得x=.
依题意,得≥.解得a≤-.
故a的取值范围为a≤-.
