27.1 图形的相似 课时练习3
图片预览

文档简介
27.1 图形的相似
专题一 开放题
1.已知三条线段的长度为,,,请你再添一条长度为 的线段,使得四条线段成比例.
2.小明家有一个矩形相框,其长、宽分别为20 cm和10 cm,小明想做一个与该相框形状完全相同的相框,手中有一根30㎝长的框料,他想以这根框料为一边,那么新的相框的另一边是多少?
专题二 操作题
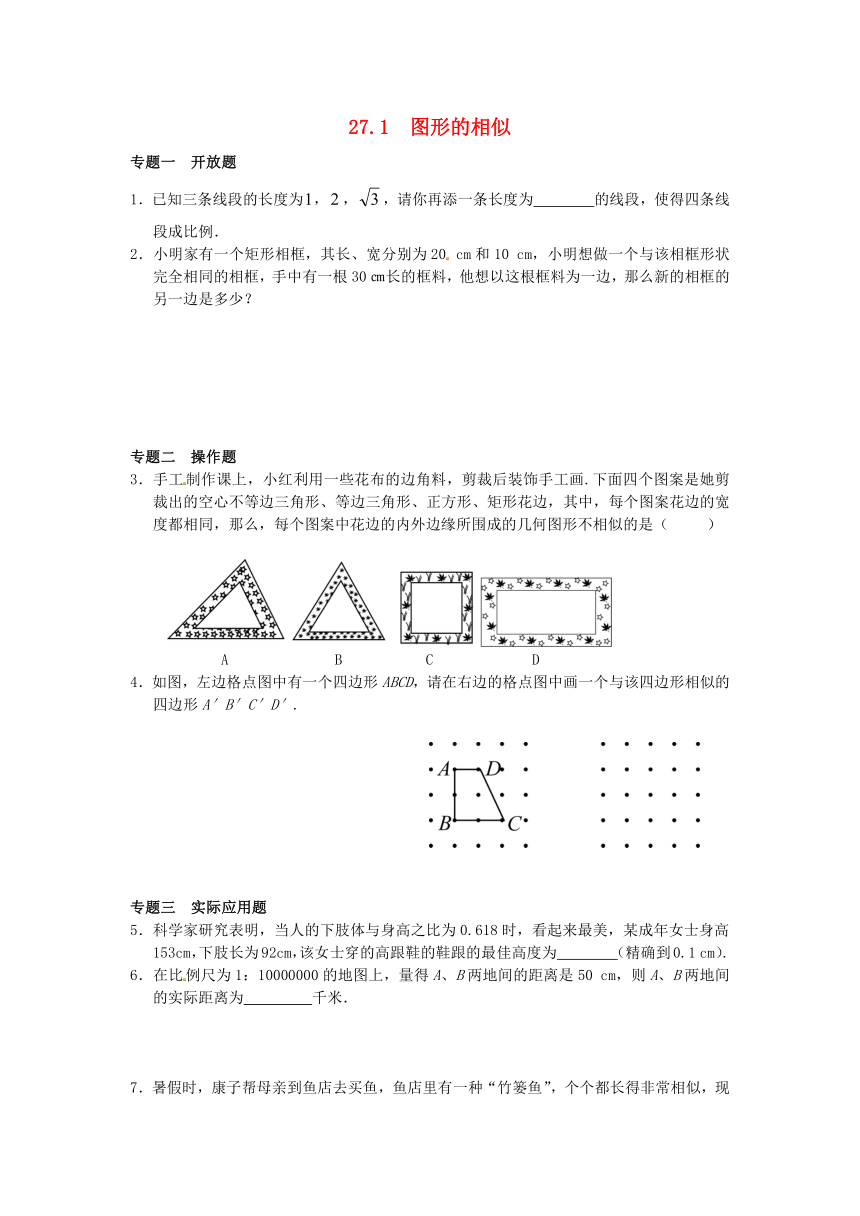
3.手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画.下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相同,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是( )
A B C D
4.如图,左边格点图中有一个四边形ABCD,请在右边的格点图中画一个与该四边形相似的四边形A′B′C′D′.
专题三 实际应用题
5.科学家研究表明,当人的下肢体与身高之比为0.618时,看起来最美,某成年女士身高153cm,下肢长为92cm,该女士穿的高跟鞋的鞋跟的最佳高度为 (精确到0.1 cm).
6.在比例尺为1:10000000的地图上,量得A、B两地间的距离是50 cm,则A、B两地间的实际距离为_________千米.
7.暑假时,康子帮母亲到鱼店去买鱼,鱼店里有一种“竹篓鱼”,个个都长得非常相似,现在根据大小有两种不同的价格,如图所示,鱼长10 cm的每条10元,鱼长18 cm的每条15元,康子不知道买哪条更好些,你看怎么办?
专题四 探究题
8.如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( ).
A. B. C. D.2
9.如图所示,一般书本的纸张是原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依次类推,若各种开本的矩形都相似,求的值.
【知识要点】
1.我们把形状相同的图形叫做相似图形.
2.对于四条线段,如果满足,我们就说这四条线段是成比例线段,
简称比例线段.
3.相似多边形对应角相等,对应边的比相等.
4.我们把多边形对应边的比称为相似比.
【温馨提示】
1.不是所有的矩形都相似,不是所有的菱形都相似.
2.判断两个多边形是否相似时,从边的比是否相等,和角是否相等两方面入手.
【方法技巧】
1.两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
2.当三角形或多边形在网格中时,要判断两图形是否相似,常常利用“网格+勾股定理”确定线段的长度.
3.图形的折叠本身也是全等问题,常常利用折叠转化相等线段和相等角.
参考答案
1. 或或(不唯一)
【解析】设所添线段的长度为,则由,可求出;
由,可求出x=;
由,可求出.
2.解:因为两个矩形相似,所以它们的对应边成比例,设另一相框边长为x㎝.
①当=时,解得x=15(㎝);
②当=时,解得x=60(㎝).
综上所述,新的相框的另一边是15 cm或60 cm.
3.D【解析】选项A中,将里面的三角形任意一条边向两边延长与外面三角形的两边相交,利用平行线的性质可以得到内、外两三角形两个角对应相等,因此两三角形相似;B中,由于任意两个等边三角形相似,因此B中两三角形相似;同理C中两正方形相似;D中内、外两矩形对应边不成比例,故两矩形不相似.
4.解:如图,将左边图形中的四边形放大一倍,得到四边形A′B′C′D′,四边形A′B′C′D′与四边形ABCD相似.
5.6.7cm 【解析】由题意知 ≈0.618,∴鞋跟高度约为6.7 cm.
6.5000 【解析】设A、B两地间的实际距离为x cm,则由50:x=1:10000000,得x=5×108(cm)=5×103千米.
7.解:因为10:10=1:1,18:15=6:5,所以买18cm长的鱼更合算.
8.B【解析】设AD=x,∵AB=1,∴FD=x﹣1,FE=1.
∵四边形EFDC与矩形ABCD相似,∴,即.
解得,(负值舍去),经检验是原方程的解.
9.解:由题意可知AD=2AE=2ED=2MN,AB=2EM,四边形EMND∽四边形EABF,则EM:MN=AE:AB,则AB∶AD=AD∶AB,则AB2∶AD2=1∶2,则AB∶AD=.
专题一 开放题
1.已知三条线段的长度为,,,请你再添一条长度为 的线段,使得四条线段成比例.
2.小明家有一个矩形相框,其长、宽分别为20 cm和10 cm,小明想做一个与该相框形状完全相同的相框,手中有一根30㎝长的框料,他想以这根框料为一边,那么新的相框的另一边是多少?
专题二 操作题
3.手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画.下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相同,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是( )
A B C D
4.如图,左边格点图中有一个四边形ABCD,请在右边的格点图中画一个与该四边形相似的四边形A′B′C′D′.
专题三 实际应用题
5.科学家研究表明,当人的下肢体与身高之比为0.618时,看起来最美,某成年女士身高153cm,下肢长为92cm,该女士穿的高跟鞋的鞋跟的最佳高度为 (精确到0.1 cm).
6.在比例尺为1:10000000的地图上,量得A、B两地间的距离是50 cm,则A、B两地间的实际距离为_________千米.
7.暑假时,康子帮母亲到鱼店去买鱼,鱼店里有一种“竹篓鱼”,个个都长得非常相似,现在根据大小有两种不同的价格,如图所示,鱼长10 cm的每条10元,鱼长18 cm的每条15元,康子不知道买哪条更好些,你看怎么办?
专题四 探究题
8.如图,已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( ).
A. B. C. D.2
9.如图所示,一般书本的纸张是原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依次类推,若各种开本的矩形都相似,求的值.
【知识要点】
1.我们把形状相同的图形叫做相似图形.
2.对于四条线段,如果满足,我们就说这四条线段是成比例线段,
简称比例线段.
3.相似多边形对应角相等,对应边的比相等.
4.我们把多边形对应边的比称为相似比.
【温馨提示】
1.不是所有的矩形都相似,不是所有的菱形都相似.
2.判断两个多边形是否相似时,从边的比是否相等,和角是否相等两方面入手.
【方法技巧】
1.两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
2.当三角形或多边形在网格中时,要判断两图形是否相似,常常利用“网格+勾股定理”确定线段的长度.
3.图形的折叠本身也是全等问题,常常利用折叠转化相等线段和相等角.
参考答案
1. 或或(不唯一)
【解析】设所添线段的长度为,则由,可求出;
由,可求出x=;
由,可求出.
2.解:因为两个矩形相似,所以它们的对应边成比例,设另一相框边长为x㎝.
①当=时,解得x=15(㎝);
②当=时,解得x=60(㎝).
综上所述,新的相框的另一边是15 cm或60 cm.
3.D【解析】选项A中,将里面的三角形任意一条边向两边延长与外面三角形的两边相交,利用平行线的性质可以得到内、外两三角形两个角对应相等,因此两三角形相似;B中,由于任意两个等边三角形相似,因此B中两三角形相似;同理C中两正方形相似;D中内、外两矩形对应边不成比例,故两矩形不相似.
4.解:如图,将左边图形中的四边形放大一倍,得到四边形A′B′C′D′,四边形A′B′C′D′与四边形ABCD相似.
5.6.7cm 【解析】由题意知 ≈0.618,∴鞋跟高度约为6.7 cm.
6.5000 【解析】设A、B两地间的实际距离为x cm,则由50:x=1:10000000,得x=5×108(cm)=5×103千米.
7.解:因为10:10=1:1,18:15=6:5,所以买18cm长的鱼更合算.
8.B【解析】设AD=x,∵AB=1,∴FD=x﹣1,FE=1.
∵四边形EFDC与矩形ABCD相似,∴,即.
解得,(负值舍去),经检验是原方程的解.
9.解:由题意可知AD=2AE=2ED=2MN,AB=2EM,四边形EMND∽四边形EABF,则EM:MN=AE:AB,则AB∶AD=AD∶AB,则AB2∶AD2=1∶2,则AB∶AD=.
