27.2.1 相似三角形的判定 课时练习2
文档属性
| 名称 | 27.2.1 相似三角形的判定 课时练习2 | 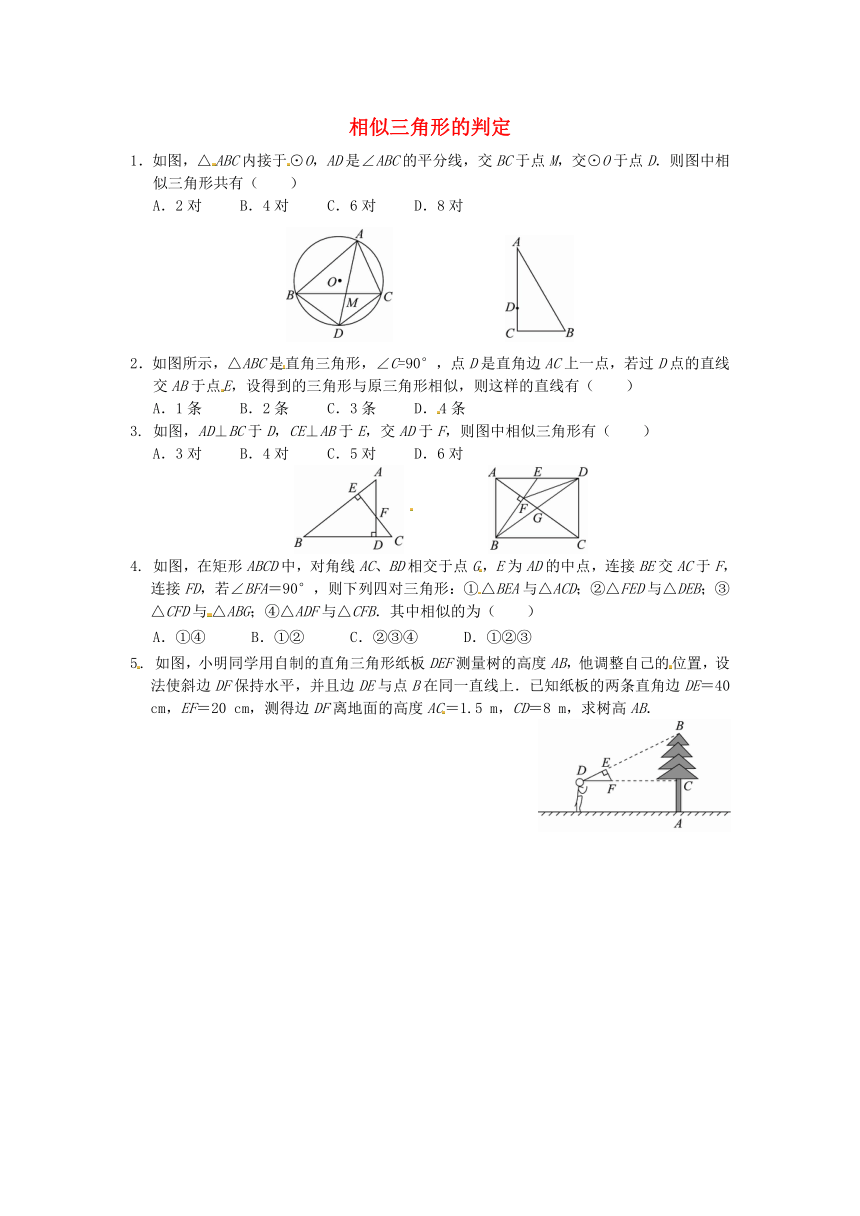 | |
| 格式 | doc | ||
| 文件大小 | 120.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 11:01:57 | ||
图片预览

文档简介
相似三角形的判定
1.如图,△ABC内接于⊙O,AD是∠ABC的平分线,交BC于点M,交⊙O于点D.则图中相似三角形共有( )
A.2对 B.4对 C.6对 D.8对
2.如图所示,△ABC是直角三角形,∠C=90°,点D是直角边AC上一点,若过D点的直线交AB于点E,设得到的三角形与原三角形相似,则这样的直线有( )
A.1条 B.2条 C.3条 D.4条
3. 如图,AD⊥BC于D,CE⊥AB于E,交AD于F,则图中相似三角形有( )
A.3对 B.4对 C.5对 D.6对
4. 如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△CFB.其中相似的为( )
A.①④ B.①② C.②③④ D.①②③
5. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,求树高AB.
参考答案
1.C
2.B
3.D
4.D
5. 解:∵∠DEF=∠BCD=90°,∠D=∠D,∴△DEF∽△DCB.
∴BC:EF=DC:DE.
∵DE=40 cm=0.4 m,EF=20 cm=0.2 m,CD=8 m,
∴BC:0.2=8:0.4,
∴BC=4 m,∴树高AB=AC+BC=1.5+4=5.5(m).
1.如图,△ABC内接于⊙O,AD是∠ABC的平分线,交BC于点M,交⊙O于点D.则图中相似三角形共有( )
A.2对 B.4对 C.6对 D.8对
2.如图所示,△ABC是直角三角形,∠C=90°,点D是直角边AC上一点,若过D点的直线交AB于点E,设得到的三角形与原三角形相似,则这样的直线有( )
A.1条 B.2条 C.3条 D.4条
3. 如图,AD⊥BC于D,CE⊥AB于E,交AD于F,则图中相似三角形有( )
A.3对 B.4对 C.5对 D.6对
4. 如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△CFB.其中相似的为( )
A.①④ B.①② C.②③④ D.①②③
5. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,求树高AB.
参考答案
1.C
2.B
3.D
4.D
5. 解:∵∠DEF=∠BCD=90°,∠D=∠D,∴△DEF∽△DCB.
∴BC:EF=DC:DE.
∵DE=40 cm=0.4 m,EF=20 cm=0.2 m,CD=8 m,
∴BC:0.2=8:0.4,
∴BC=4 m,∴树高AB=AC+BC=1.5+4=5.5(m).
