人教版七年级数学上册2.2 整式的加减《合并同类项》教学设计 (表格式)
文档属性
| 名称 | 人教版七年级数学上册2.2 整式的加减《合并同类项》教学设计 (表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 137.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 07:02:31 | ||
图片预览

文档简介
合并同类项
一、教学目标
(1)知识与技能
1、了解同类项的概念,能识别同类项;
2、学会合并同类项,并知道合并同类项所依据的运算律.
(2)过程与方法
让学生经历观察、分析、归纳的的过程,进一步培养学生的“分类”“整体”“方程”的数学思想。
(3)情感、态度、价值观
1、积极营造亲切和谐的课堂氛围,激励全体学生积极参与教学活动。
2、进一步培养学生团结协助、严谨求实的学习作风和勇于创新的精神。
二、教学重、难点
重点:同类项的概念,合并同类项的定义和法则;
难点:会合并同类项。
三、教学过程设计与分析
在这堂课的教学中,采用“以学为主”的设计 ( http: / / www.21cnjy.com )模式。根据学习任务、学生分析和教学目标,采取以下的教学流程:创设情境—建构新知——例题板演——模仿练习——归纳小结——当堂检测。通过教师引导讲授和学生归纳,以讨论法、谈话法组织整个教学过程。
教学过程教学过程 教学环节 内容 设计意图
同舟竞技 提出生活中的分类,数学课上也有分类,复习整式的分类同舟竞技:规则:请任意一名同学任意报一个关于x的一位整数,求所给代数式-x2 +2x +x2 –x -1的值,看谁算得快! 复习旧知识,为新知识作铺垫,激发学生的求知欲
创设情境一 一、同类项自主尝试:观察下列各单项式,请你根据这些单项式的特征对它们进行分类,并说出你的分类标准. ( http: / / www.21cnjy.com ) 目的在于引发和提高学生学习的积极性,启发学生的探索欲望,加强学科联系,并注意联系生活,同时为本课学习做好准备和铺垫。
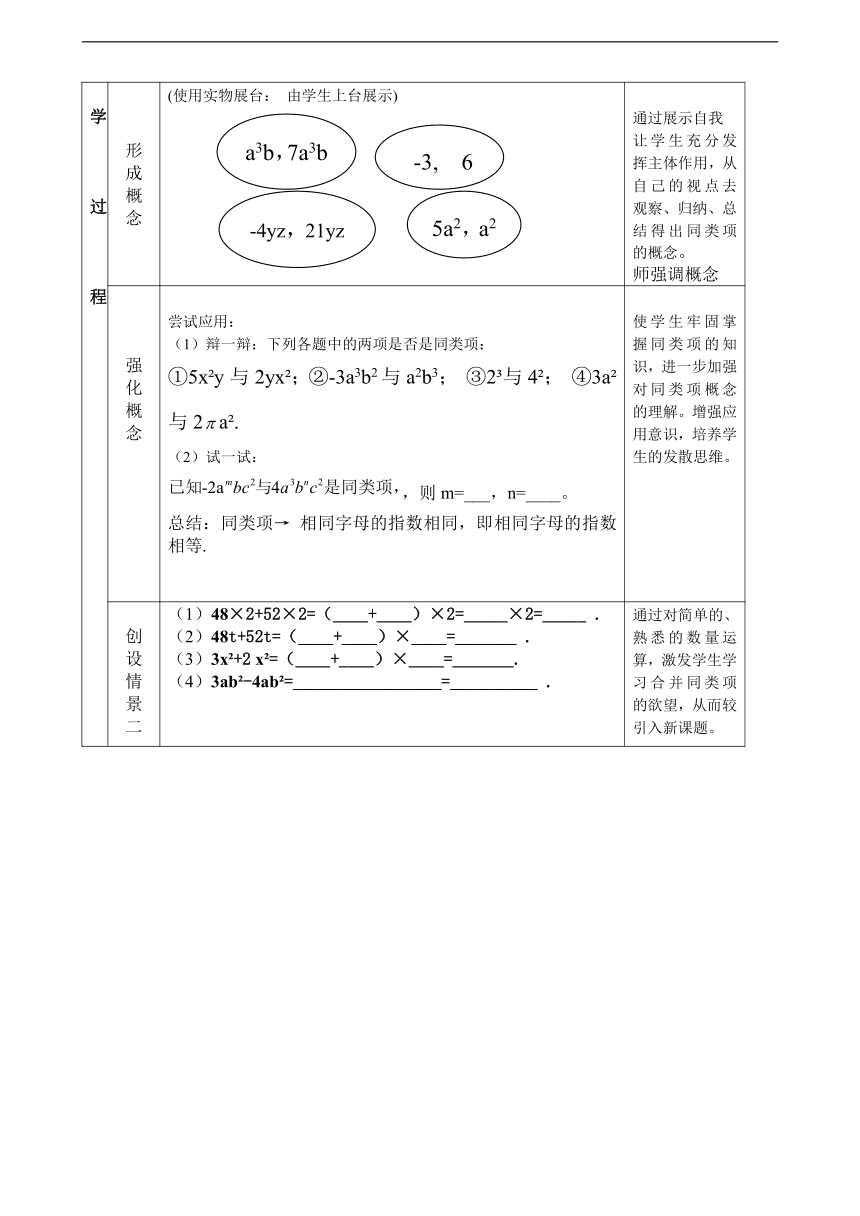
形成概念 (使用实物展台: 由学生上台展示) 通过展示自我让学生充分发挥主体作用,从自己的视点去观察、归纳、总结得出同类项的概念。师强调概念
强化概念 尝试应用:(1)辩一辩:下列各题中的两项是否是同类项:①5x y与2yx ;②-3a3b2与a2b3; ③2 与4 ; ④3a 与2a .(2)试一试:,则m=___,n=____。总结:同类项→ 相同字母的指数相同,即相同字母的指数相等. 使学生牢固掌握同类项的知识,进一步加强对同类项概念的理解。增强应用意识,培养学生的发散思维。
创设情景二 (1)48×2+52×2=(____+____)×2=_____×2=_____ .(2)48t+52t=(____+____)×____=_______ .(3)3x +2 x =(____+____)×____=_______.(4)3ab -4ab =_________________=__________ . 通过对简单的、熟悉的数量运算,激发学生学习合并同类项的欲望,从而较引入新课题。
层层追问引出法则合并同类项的步骤巩固法则尝试训练 我们通过逆用乘法分配律的方法,就完成合并同类项了。 只把系数相加 (一变)合并同类项 字母和字母的指数不变 (两不变)尝试应用:下面合并同类项是否正确。 (1)a+a=2a2, (2)3a+2b=5ab, (3)5y2-3y2=2, (4)4x2y-5x2y= -x2y. 例1 计 4a2+3b2+2ab-4a2-4b2 我们应该先找同类项;找 我们把交换位置把同类项放在一起,换然后把同类项结合在一起,用括号括起来 最后合并同类项。 小试牛刀:合并下列各式中的同类项:-x2 +2x +x2 –x -1 合并同类项就是给多项式”减肥”,使运算更简便 例2 求多项式 的值,其中a=- b=2,c=-3 强调:在代数式求值时,先合并同类项,再求值。 牛刀小试:先化简,再求值: 求多项式 的值,其中x= 分解难度,设计过渡问题,使学生能自然的感受法则的探索过程。以一道例题的训练为桥梁来得出合并同类项的一般步骤。体现新课程中以学生为主,注重学生参与的理念。求多项式的值,常常先合并同类项,化简后再求值,这样比较简便。
教学过程 课堂小结教师总结当堂检测 这实际就是整式的加减(板书: ( http: / / www.21cnjy.com )整式的加减),整式的加减就是逆用乘法的分配律进行合并同类项,其基本步骤是先找同类项,再交换位置把同类项放在一起,通过添加括号将同类项结合在一起,最后合并同类项.一要注意符号,二要灵活使用括号。这儿也渗透着我们数学上的重要的分类讨论的思想。还有我们进行整式的加减计算就是要合并化简到不能再化简为止。板书设计: 字母相同 整 分类思想 相同字母的指数也相同 同类项式 常数项的 逆用分配率 只把系数相加 合并同类项加 找,移,并 字母和字母的指数不变减 1、选择题: (1)下列各组代数式中,是同类项的是 ( ) A.5xy与xy B.一5xy与yx C.5x与yx D.8与x(2)下列运算中结果正确的是 ( ) A.3a+2b=5ab B.5y-3y=2 C.-3x+5x=-8x D.3x2y-2x2y=x2y2、合并同类项 3求下列式子的值3x-4x2+7-3x+2x2+1,其中x=-3 小组讨论进一步让学生巩固基本知识,渗透数学分类思想;使知识结构更完善。
-3, 6
a3b,7a3b
-4yz,21yz
5a2,a2
两相同
两无关
一变
两不变
一、教学目标
(1)知识与技能
1、了解同类项的概念,能识别同类项;
2、学会合并同类项,并知道合并同类项所依据的运算律.
(2)过程与方法
让学生经历观察、分析、归纳的的过程,进一步培养学生的“分类”“整体”“方程”的数学思想。
(3)情感、态度、价值观
1、积极营造亲切和谐的课堂氛围,激励全体学生积极参与教学活动。
2、进一步培养学生团结协助、严谨求实的学习作风和勇于创新的精神。
二、教学重、难点
重点:同类项的概念,合并同类项的定义和法则;
难点:会合并同类项。
三、教学过程设计与分析
在这堂课的教学中,采用“以学为主”的设计 ( http: / / www.21cnjy.com )模式。根据学习任务、学生分析和教学目标,采取以下的教学流程:创设情境—建构新知——例题板演——模仿练习——归纳小结——当堂检测。通过教师引导讲授和学生归纳,以讨论法、谈话法组织整个教学过程。
教学过程教学过程 教学环节 内容 设计意图
同舟竞技 提出生活中的分类,数学课上也有分类,复习整式的分类同舟竞技:规则:请任意一名同学任意报一个关于x的一位整数,求所给代数式-x2 +2x +x2 –x -1的值,看谁算得快! 复习旧知识,为新知识作铺垫,激发学生的求知欲
创设情境一 一、同类项自主尝试:观察下列各单项式,请你根据这些单项式的特征对它们进行分类,并说出你的分类标准. ( http: / / www.21cnjy.com ) 目的在于引发和提高学生学习的积极性,启发学生的探索欲望,加强学科联系,并注意联系生活,同时为本课学习做好准备和铺垫。
形成概念 (使用实物展台: 由学生上台展示) 通过展示自我让学生充分发挥主体作用,从自己的视点去观察、归纳、总结得出同类项的概念。师强调概念
强化概念 尝试应用:(1)辩一辩:下列各题中的两项是否是同类项:①5x y与2yx ;②-3a3b2与a2b3; ③2 与4 ; ④3a 与2a .(2)试一试:,则m=___,n=____。总结:同类项→ 相同字母的指数相同,即相同字母的指数相等. 使学生牢固掌握同类项的知识,进一步加强对同类项概念的理解。增强应用意识,培养学生的发散思维。
创设情景二 (1)48×2+52×2=(____+____)×2=_____×2=_____ .(2)48t+52t=(____+____)×____=_______ .(3)3x +2 x =(____+____)×____=_______.(4)3ab -4ab =_________________=__________ . 通过对简单的、熟悉的数量运算,激发学生学习合并同类项的欲望,从而较引入新课题。
层层追问引出法则合并同类项的步骤巩固法则尝试训练 我们通过逆用乘法分配律的方法,就完成合并同类项了。 只把系数相加 (一变)合并同类项 字母和字母的指数不变 (两不变)尝试应用:下面合并同类项是否正确。 (1)a+a=2a2, (2)3a+2b=5ab, (3)5y2-3y2=2, (4)4x2y-5x2y= -x2y. 例1 计 4a2+3b2+2ab-4a2-4b2 我们应该先找同类项;找 我们把交换位置把同类项放在一起,换然后把同类项结合在一起,用括号括起来 最后合并同类项。 小试牛刀:合并下列各式中的同类项:-x2 +2x +x2 –x -1 合并同类项就是给多项式”减肥”,使运算更简便 例2 求多项式 的值,其中a=- b=2,c=-3 强调:在代数式求值时,先合并同类项,再求值。 牛刀小试:先化简,再求值: 求多项式 的值,其中x= 分解难度,设计过渡问题,使学生能自然的感受法则的探索过程。以一道例题的训练为桥梁来得出合并同类项的一般步骤。体现新课程中以学生为主,注重学生参与的理念。求多项式的值,常常先合并同类项,化简后再求值,这样比较简便。
教学过程 课堂小结教师总结当堂检测 这实际就是整式的加减(板书: ( http: / / www.21cnjy.com )整式的加减),整式的加减就是逆用乘法的分配律进行合并同类项,其基本步骤是先找同类项,再交换位置把同类项放在一起,通过添加括号将同类项结合在一起,最后合并同类项.一要注意符号,二要灵活使用括号。这儿也渗透着我们数学上的重要的分类讨论的思想。还有我们进行整式的加减计算就是要合并化简到不能再化简为止。板书设计: 字母相同 整 分类思想 相同字母的指数也相同 同类项式 常数项的 逆用分配率 只把系数相加 合并同类项加 找,移,并 字母和字母的指数不变减 1、选择题: (1)下列各组代数式中,是同类项的是 ( ) A.5xy与xy B.一5xy与yx C.5x与yx D.8与x(2)下列运算中结果正确的是 ( ) A.3a+2b=5ab B.5y-3y=2 C.-3x+5x=-8x D.3x2y-2x2y=x2y2、合并同类项 3求下列式子的值3x-4x2+7-3x+2x2+1,其中x=-3 小组讨论进一步让学生巩固基本知识,渗透数学分类思想;使知识结构更完善。
-3, 6
a3b,7a3b
-4yz,21yz
5a2,a2
两相同
两无关
一变
两不变
