2021-2022学年北师大版七年级数学下册第四章三角形复习与回顾同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册第四章三角形复习与回顾同步练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 928.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 00:00:00 | ||
图片预览



文档简介
第四章复习与回顾(1)
一、基础性作业(必做题)
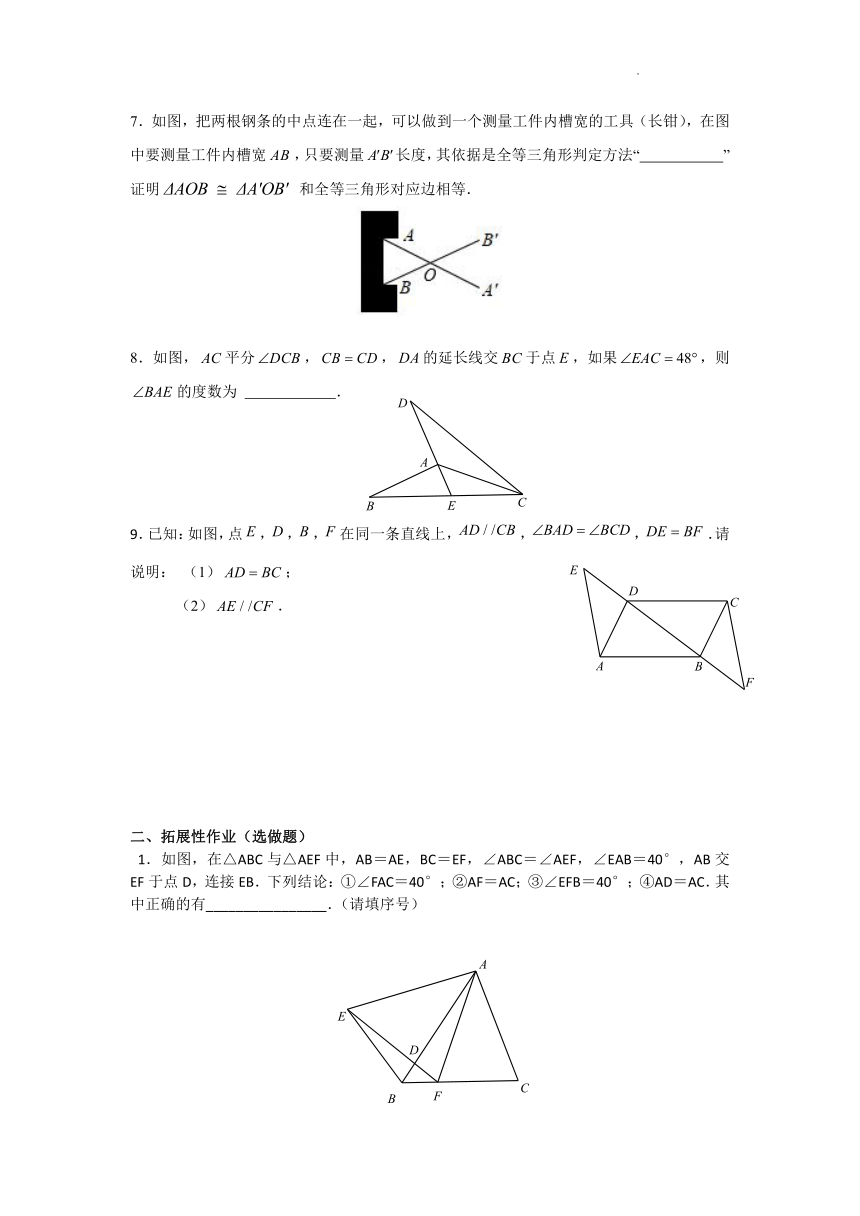
1.下列长度的各组线段中,能组成三角形的是( )
A.1,2,3 B.2,3,5 C.3,4,8 D.3,4,5
2.若一个三角形的三个内角的度数之比为1:3:4,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
3. 如图所示,在中,、、分别为、、的中点,且,则的面积等于
A. B. C. D.
4. 如图,工人师傅砌门时,常用木条固定门框,使其不变形,根据是三角形具有 .
5. 如图,已知,,那么图中共有 对全等三角形.
6. 如图,已知点、、、在同一直线上,,,则添加条件 ,可以判断.
7.如图,把两根钢条的中点连在一起,可以做到一个测量工件内槽宽的工具(长钳),在图中要测量工件内槽宽,只要测量长度,其依据是全等三角形判定方法“ ”证明 和全等三角形对应边相等.
8.如图,平分,,的延长线交于点,如果,则的度数为 .
9.已知:如图,点,,,在同一条直线上,,,.请说明: (1);
(2).
二、拓展性作业(选做题)
1.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EFB=40°;④AD=AC.其中正确的有________________.(请填序号)
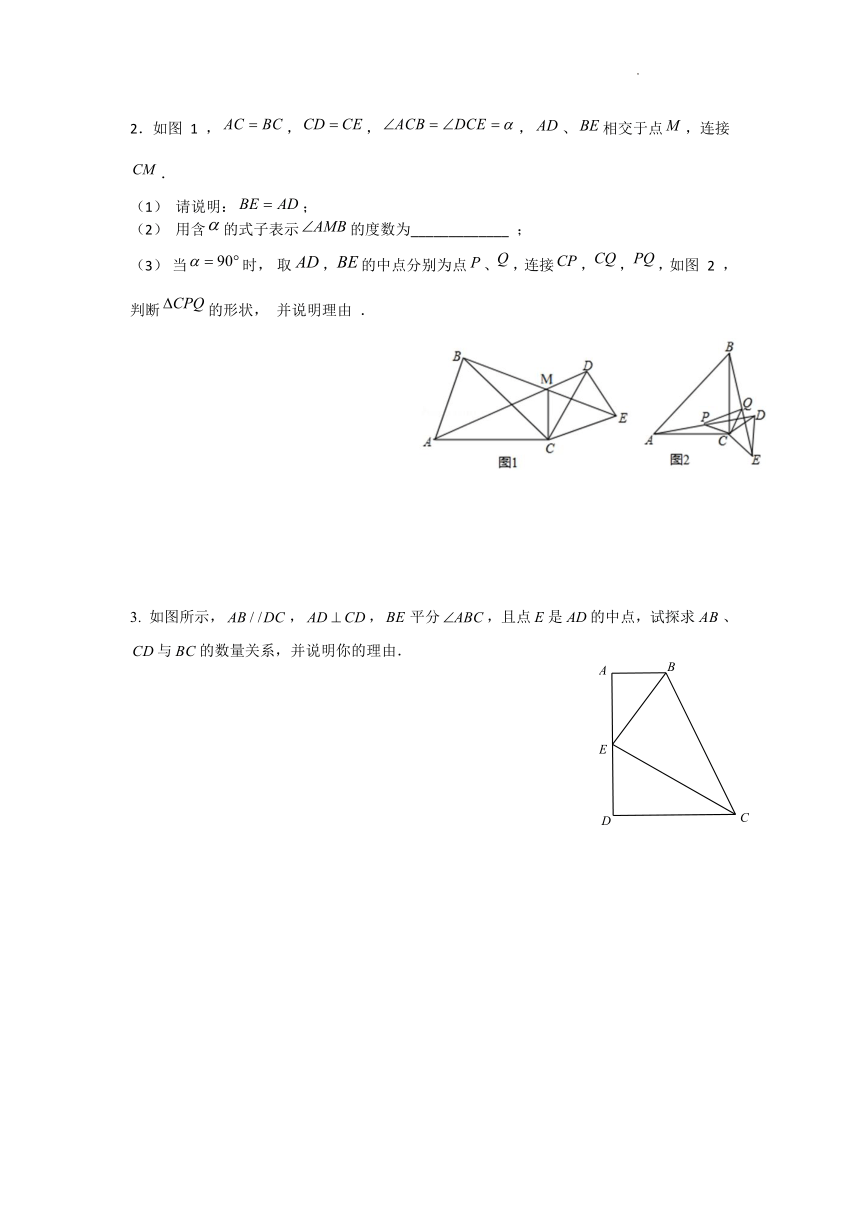
2.如图 1 ,,,,、相交于点,连接.
(1) 请说明:;
(2) 用含的式子表示的度数为_____________ ;
(3) 当时, 取,的中点分别为点、,连接,,,如图 2 ,判断的形状, 并说明理由 .
3. 如图所示,,,平分,且点是的中点,试探求、与的数量关系,并说明你的理由.
第四章复习与回顾 参考答案
一、基础性作业(必做题)
1.D.
2.B.
3.A
4.稳定性.
5.3 .
6.∠AFB=∠DEC(或AB=DC).
7.SAS .
8.84°.
9.证明:(1),
.
在和中
,
;
(2),,,
.
在和中
.
,
.
二、拓展性作业(选做题)
1.①②③
2.解:(1) 如图 1 ,,
,
在和中,
,
,
;
(2);
(3)为等腰直角三角形 .
证明: 如图 2 ,由 (1) 可得,,
,的中点分别为点、,
,
,
,
在和中,
,
,
,且,
又,
,
,
为等腰直角三角形 .
3.解:,理由如下:过作于,
平分,
.
在与中,
,
,
.
同理可得:,
,
,
.
第四章复习与回顾(2)
一、基础性作业(必做题)
1. 如图所示的网格由边长相同的小正方形组成,点、、、、、、在小正方形的顶点上,则的重心是
A.点 B.点 C.点 D.点
2. 如图,在中,,,是高,是角平分线,则的度数为
A. B. C. D.
3. 打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是
A.带①③去 B.带②③去 C.带③④去 D.带②④去
4. 在直角中,,是边上的高线,且,,,则的长为_______________________.
5. 在和中,其中,则下列条件:①,;②,;③,;④,;⑤,.其中能够判定这两个三角形全等的是_________________.(填序号)
6. 如图,在中,,,,以为圆心,以适当的长为半径作弧,交于点,交于点.分别以,为圆心,以大于的长为半径作弧,两弧在的内部相交于点,作射线,交于点,点在边上,,连接,则的周长为 .
7.如图,点、、、在一条直线上(点,之间不能直接测量),点,在的异侧,如果测得,,.若,,则的长度为 .
8. 如图,在中,为上一点,为的中点,连接并延长至点,连接,已知.
(1)求证:为的中点;
(2)若,连接,平分,平分,求的度数.
二、拓展性作业(选做题)
1. 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是 .
第1题 第2题
2. 如图,在中,,,则边上的中线的长的取值范围是 .
3.在一个三角形中,如果一个角是另一个角的2倍,这样的三角形我们称之为“倍角三角形”.如图,中,,点是线段上一点(不与、重合),连接.
(1)当时;
①若,则 “倍角三角形”(填“是”或“否” ;
②若是“倍角三角形”,求的度数;
(2)当、、都是“倍角三角形”时,则的度数为____________.
第四章复习与回顾 参考答案
一、基础性作业(必做题)
1.A.
2.B.
3.A.
4..
5.①②④.
6.12 .
7.4 .
8.(1)证明:,
,
为的中点,
.
在和中,
,
,
.
即为的中点;
(2)解:,,
,,
平分,
,
.
二、拓展性作业(选做题)
1.80°.
2.23.解:解:(1)①,,
,
,
,
,
,
是“倍角三角形”,
故答案为:是.
②,是“倍角三角形”,
内角的度数分别是,,,
或,
或.
(2)如图中,当是等腰直角三角形,时,满足条件,此时.
如图中,当,时,满足条件,此时.
如图中,当,时,满足条件,此时.
如图中,当,时,满足条件,此时.
如图中,当,时,满足条件,此时.
综上所述,满足条件的的值为或或或或.
一、基础性作业(必做题)
1.下列长度的各组线段中,能组成三角形的是( )
A.1,2,3 B.2,3,5 C.3,4,8 D.3,4,5
2.若一个三角形的三个内角的度数之比为1:3:4,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
3. 如图所示,在中,、、分别为、、的中点,且,则的面积等于
A. B. C. D.
4. 如图,工人师傅砌门时,常用木条固定门框,使其不变形,根据是三角形具有 .
5. 如图,已知,,那么图中共有 对全等三角形.
6. 如图,已知点、、、在同一直线上,,,则添加条件 ,可以判断.
7.如图,把两根钢条的中点连在一起,可以做到一个测量工件内槽宽的工具(长钳),在图中要测量工件内槽宽,只要测量长度,其依据是全等三角形判定方法“ ”证明 和全等三角形对应边相等.
8.如图,平分,,的延长线交于点,如果,则的度数为 .
9.已知:如图,点,,,在同一条直线上,,,.请说明: (1);
(2).
二、拓展性作业(选做题)
1.如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EFB=40°;④AD=AC.其中正确的有________________.(请填序号)
2.如图 1 ,,,,、相交于点,连接.
(1) 请说明:;
(2) 用含的式子表示的度数为_____________ ;
(3) 当时, 取,的中点分别为点、,连接,,,如图 2 ,判断的形状, 并说明理由 .
3. 如图所示,,,平分,且点是的中点,试探求、与的数量关系,并说明你的理由.
第四章复习与回顾 参考答案
一、基础性作业(必做题)
1.D.
2.B.
3.A
4.稳定性.
5.3 .
6.∠AFB=∠DEC(或AB=DC).
7.SAS .
8.84°.
9.证明:(1),
.
在和中
,
;
(2),,,
.
在和中
.
,
.
二、拓展性作业(选做题)
1.①②③
2.解:(1) 如图 1 ,,
,
在和中,
,
,
;
(2);
(3)为等腰直角三角形 .
证明: 如图 2 ,由 (1) 可得,,
,的中点分别为点、,
,
,
,
在和中,
,
,
,且,
又,
,
,
为等腰直角三角形 .
3.解:,理由如下:过作于,
平分,
.
在与中,
,
,
.
同理可得:,
,
,
.
第四章复习与回顾(2)
一、基础性作业(必做题)
1. 如图所示的网格由边长相同的小正方形组成,点、、、、、、在小正方形的顶点上,则的重心是
A.点 B.点 C.点 D.点
2. 如图,在中,,,是高,是角平分线,则的度数为
A. B. C. D.
3. 打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是
A.带①③去 B.带②③去 C.带③④去 D.带②④去
4. 在直角中,,是边上的高线,且,,,则的长为_______________________.
5. 在和中,其中,则下列条件:①,;②,;③,;④,;⑤,.其中能够判定这两个三角形全等的是_________________.(填序号)
6. 如图,在中,,,,以为圆心,以适当的长为半径作弧,交于点,交于点.分别以,为圆心,以大于的长为半径作弧,两弧在的内部相交于点,作射线,交于点,点在边上,,连接,则的周长为 .
7.如图,点、、、在一条直线上(点,之间不能直接测量),点,在的异侧,如果测得,,.若,,则的长度为 .
8. 如图,在中,为上一点,为的中点,连接并延长至点,连接,已知.
(1)求证:为的中点;
(2)若,连接,平分,平分,求的度数.
二、拓展性作业(选做题)
1. 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是 .
第1题 第2题
2. 如图,在中,,,则边上的中线的长的取值范围是 .
3.在一个三角形中,如果一个角是另一个角的2倍,这样的三角形我们称之为“倍角三角形”.如图,中,,点是线段上一点(不与、重合),连接.
(1)当时;
①若,则 “倍角三角形”(填“是”或“否” ;
②若是“倍角三角形”,求的度数;
(2)当、、都是“倍角三角形”时,则的度数为____________.
第四章复习与回顾 参考答案
一、基础性作业(必做题)
1.A.
2.B.
3.A.
4..
5.①②④.
6.12 .
7.4 .
8.(1)证明:,
,
为的中点,
.
在和中,
,
,
.
即为的中点;
(2)解:,,
,,
平分,
,
.
二、拓展性作业(选做题)
1.80°.
2.2
,
,
,
,
,
是“倍角三角形”,
故答案为:是.
②,是“倍角三角形”,
内角的度数分别是,,,
或,
或.
(2)如图中,当是等腰直角三角形,时,满足条件,此时.
如图中,当,时,满足条件,此时.
如图中,当,时,满足条件,此时.
如图中,当,时,满足条件,此时.
如图中,当,时,满足条件,此时.
综上所述,满足条件的的值为或或或或.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
