北师大版七年级数学下册 5.3 角的轴对称性 课件(共28张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 5.3 角的轴对称性 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
第五章
生活中的轴对称
5.3 简单的轴对称图形(三)
北师大版·数学·七年级下册
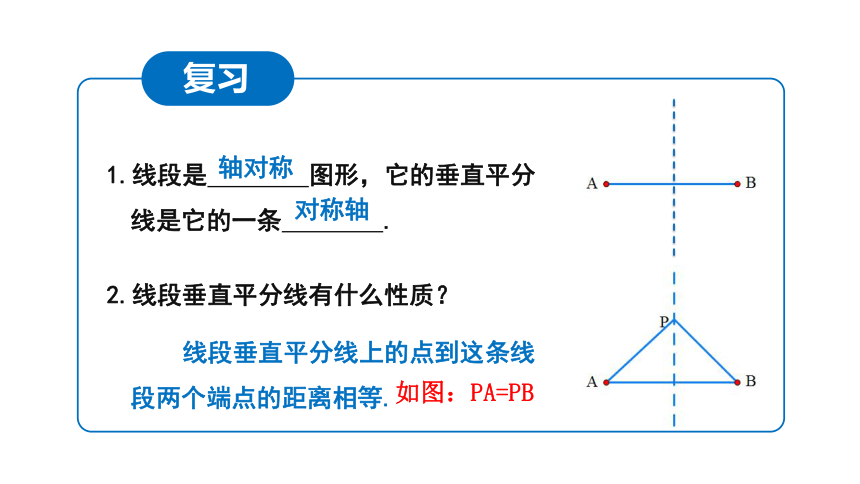
复习
1.线段是 图形,它的垂直平分线是它的一条 .
2.线段垂直平分线有什么性质?
线段垂直平分线上的点到这条线段两个端点的距离相等.
轴对称
对称轴
如图:PA=PB
1
情景导入,初步认知
2
思考探究,获取新知
3
深化理解
4
课堂小结
5
课后作业
角Angle
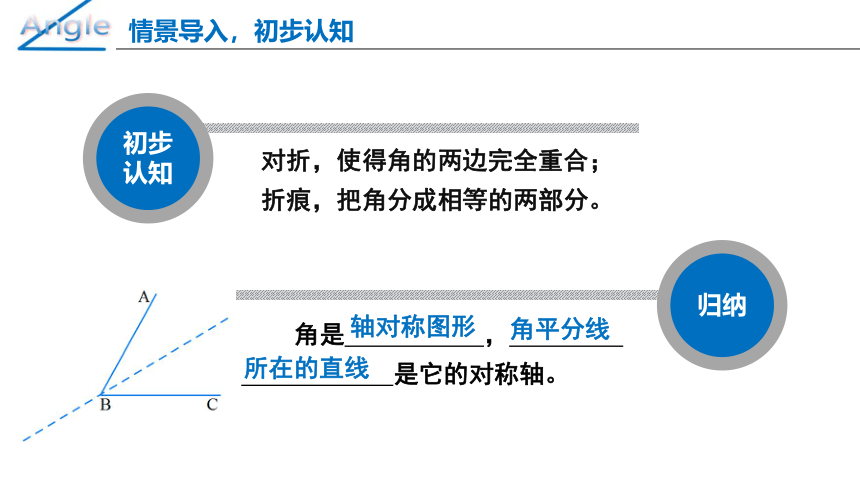
情景导入
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
对折
(视频)
打开纸片,看看折痕与这个角有何关系?
情景导入,初步认知
角平分线
所在的直线
初步认知
对折,使得角的两边完全重合;
折痕,把角分成相等的两部分。
归纳
角是 , .
是它的对称轴。
情景导入,初步认知
轴对称图形
1
年度工作概述
2
思考探究,获取新知
3
成功项目展示
4
工作存在不足
5
明年工作计划
角
Angle
情景导入,初步认知
深化理解
课堂小结
课后作业
探究1
做一做
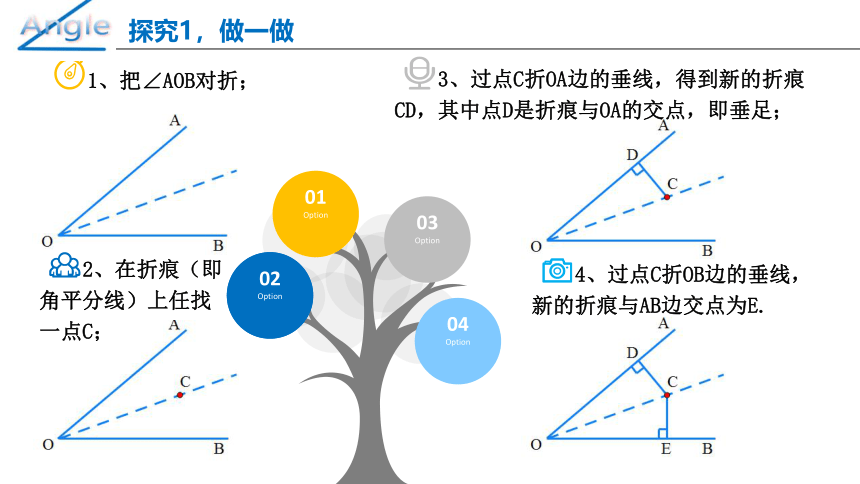
拿出准备好的角(纸片),标上∠AOB,并按以下步骤操作.
02
Option here
01
Option
1、把∠AOB对折;
03
Option
04
Option
探究1,做一做
2、在折痕(即角平分线)上任找一点C;
3、过点C折OA边的垂线,得到新的折痕CD,其中点D是折痕与OA的交点,即垂足;
4、过点C折OB边的垂线,新的折痕与AB边交点为E.
02
Option
Observe
探究1,做一做
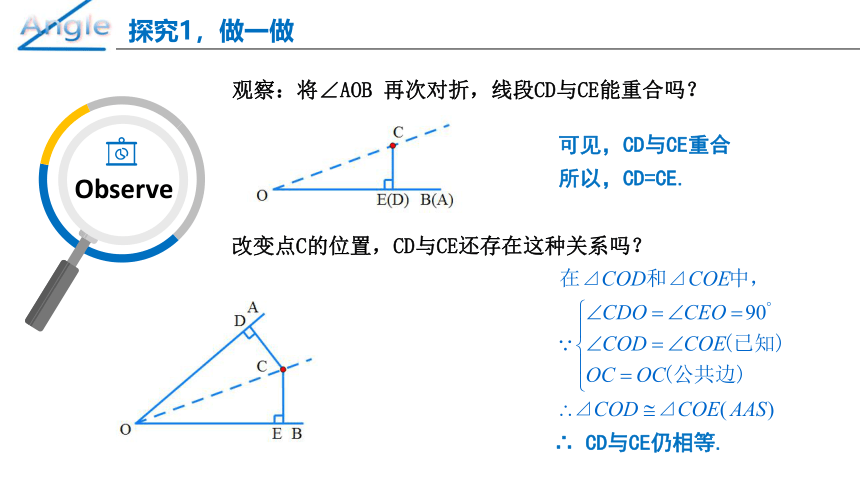
观察:将∠AOB 再次对折,线段CD与CE能重合吗?
改变点C的位置,CD与CE还存在这种关系吗?
可见,CD与CE重合
所以,CD=CE.
∴ CD与CE仍相等.
用符号语言表示
必须找全推理的三个理由。
角平分线的性质
角平分线上的点 .
探究1,归纳
E
D
拓展
到这个角的两边的距离相等
探究1,归纳
延伸
角平分线的性质,为我们“证明两线段相等”,又提供了新的方法与途径。
运用新知
练习
1、如图,在Rt⊿ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
解:DE=DC.
理由是:射线BD是∠ABC的平分线,点D到角两边BA,BC的距离分别是线段DE,DC的长,所以DE=DC.
运用新知
练习
2、如图,在⊿ABC中,∠C=90°,AD是∠BAC的平分线,BC=8cm,BD=5cm,那么点D到直线AB的距离是 .
∟
E
析:DE=DC=BC-BD=8-5=3(cm).
作图
例:利用尺规,作∠AOB的平分线.
探究2,尺规作角平分线
已知:∠AOB.
求作:射线OC,使∠AOC=∠BOC.
A
B
O
探究2,尺规作角平分线
已知:∠AOB.
求作:射线OC,使∠AOC=∠BOC.
尺规作图
作法
尺规作图
微课
尺规作图
证明
尺规作图
注意事项
已知:∠AOB.
求作:射线OC,使∠AOC=∠BOC.
尺规作角平分线
A
B
O
D
E
C
作法:
1.在OA和OB上分别截取OD,OE,使OD=OE.
2.分别以D,E为圆心、以大于 的长为半径作弧,两弧在∠AOB内交于点C.
3.作射线OC.
OC就是∠AOB的平分线.
A
B
O
B
A
O
D
E
C
由已知得,OD=OE、 DC=EC
在⊿OCD和⊿OCE中,
OD=OE(已知)
DC=EC(已知)
OC=OC(公共边)
∴⊿OCD ≌⊿OCE(SSS)
∴∠COD =∠COE
∴OC是∠AOB的平分线.
∵
证明:
已知在∠AOB中,OD=OE,DC=EC. 求证:OC是∠AOB的平分线.
尺规作角平分线
尺规作图注意事项:
尺规作角平分线
1、初中阶段,尺规作图不要求学生写作法,但学生应能说明其中的道理,即以操作和理解为主;
2、保留作图痕迹;
3、在空白处注明:“如图,xxx为所求作。”
运用新知
练习
3、先任意画一个角,然后利用尺规将它四等分.
(要求:写出已知、求作,利用尺规作图)
1
2
3
4
5
目录
CONTENTS
思考探究,获取新知
情景导入,初步认知
深化理解
课堂小结
课后作业
深化理解
习题
1、如图,已知⊿ABC内一点P到∠A的两边的距离相等,且PA=PB,则P点如何确定?
P
·
析:先作出∠BAC的平分线,
再作出线段AB的中垂线,
两线交点P就是所要确定的点.
∟
习题
2、如图,在⊿ABC中,BD是三角形的角平分线,BC=12cm,BA=8cm,点D到直线BC的距离等于4cm,求⊿ABC的面积.
深化理解
析:过D作DF垂直AB,垂足为F,
则,DF=DE=4
∴S⊿ABC = S⊿ABD+S⊿CBD
=(AB×DF+BC×DE)÷2
=40(cm2)
∟
F
习题
3、如图,BD是∠ABC的平分线,BA=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别为M,N. 试说明 PM=PN.
深化理解
析:先证明⊿ABD ≌⊿CBD(SAS),
得, ∠ADB =∠CDB,
根据角平分线的性质,得
PM = PN.
1
2
3
4
5
目录
CONTENTS
思考探究,获取新知
情景导入,初步认知
深化理解
课堂小结
课后作业
归纳1
角是轴对称图形,角平分线所在的直线是它的对称轴.
课堂小结
归纳2
角平分线上的点到这个角的两边的距离相等.
注意:这里的距离指的是“点到线的距离”
归纳3
掌握尺规作角平分线的方法与步骤.
1
2
3
目录
CONTENTS
思考探究,获取新知
情景导入,初步认知
深化理解
课堂小结
课后作业
4
5
课本 P127 习题5.5
第 2、3题
课后作业
下一节再见
第五章
生活中的轴对称
5.3 简单的轴对称图形(三)
北师大版·数学·七年级下册
复习
1.线段是 图形,它的垂直平分线是它的一条 .
2.线段垂直平分线有什么性质?
线段垂直平分线上的点到这条线段两个端点的距离相等.
轴对称
对称轴
如图:PA=PB
1
情景导入,初步认知
2
思考探究,获取新知
3
深化理解
4
课堂小结
5
课后作业
角Angle
情景导入
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
对折
(视频)
打开纸片,看看折痕与这个角有何关系?
情景导入,初步认知
角平分线
所在的直线
初步认知
对折,使得角的两边完全重合;
折痕,把角分成相等的两部分。
归纳
角是 , .
是它的对称轴。
情景导入,初步认知
轴对称图形
1
年度工作概述
2
思考探究,获取新知
3
成功项目展示
4
工作存在不足
5
明年工作计划
角
Angle
情景导入,初步认知
深化理解
课堂小结
课后作业
探究1
做一做
拿出准备好的角(纸片),标上∠AOB,并按以下步骤操作.
02
Option here
01
Option
1、把∠AOB对折;
03
Option
04
Option
探究1,做一做
2、在折痕(即角平分线)上任找一点C;
3、过点C折OA边的垂线,得到新的折痕CD,其中点D是折痕与OA的交点,即垂足;
4、过点C折OB边的垂线,新的折痕与AB边交点为E.
02
Option
Observe
探究1,做一做
观察:将∠AOB 再次对折,线段CD与CE能重合吗?
改变点C的位置,CD与CE还存在这种关系吗?
可见,CD与CE重合
所以,CD=CE.
∴ CD与CE仍相等.
用符号语言表示
必须找全推理的三个理由。
角平分线的性质
角平分线上的点 .
探究1,归纳
E
D
拓展
到这个角的两边的距离相等
探究1,归纳
延伸
角平分线的性质,为我们“证明两线段相等”,又提供了新的方法与途径。
运用新知
练习
1、如图,在Rt⊿ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
解:DE=DC.
理由是:射线BD是∠ABC的平分线,点D到角两边BA,BC的距离分别是线段DE,DC的长,所以DE=DC.
运用新知
练习
2、如图,在⊿ABC中,∠C=90°,AD是∠BAC的平分线,BC=8cm,BD=5cm,那么点D到直线AB的距离是 .
∟
E
析:DE=DC=BC-BD=8-5=3(cm).
作图
例:利用尺规,作∠AOB的平分线.
探究2,尺规作角平分线
已知:∠AOB.
求作:射线OC,使∠AOC=∠BOC.
A
B
O
探究2,尺规作角平分线
已知:∠AOB.
求作:射线OC,使∠AOC=∠BOC.
尺规作图
作法
尺规作图
微课
尺规作图
证明
尺规作图
注意事项
已知:∠AOB.
求作:射线OC,使∠AOC=∠BOC.
尺规作角平分线
A
B
O
D
E
C
作法:
1.在OA和OB上分别截取OD,OE,使OD=OE.
2.分别以D,E为圆心、以大于 的长为半径作弧,两弧在∠AOB内交于点C.
3.作射线OC.
OC就是∠AOB的平分线.
A
B
O
B
A
O
D
E
C
由已知得,OD=OE、 DC=EC
在⊿OCD和⊿OCE中,
OD=OE(已知)
DC=EC(已知)
OC=OC(公共边)
∴⊿OCD ≌⊿OCE(SSS)
∴∠COD =∠COE
∴OC是∠AOB的平分线.
∵
证明:
已知在∠AOB中,OD=OE,DC=EC. 求证:OC是∠AOB的平分线.
尺规作角平分线
尺规作图注意事项:
尺规作角平分线
1、初中阶段,尺规作图不要求学生写作法,但学生应能说明其中的道理,即以操作和理解为主;
2、保留作图痕迹;
3、在空白处注明:“如图,xxx为所求作。”
运用新知
练习
3、先任意画一个角,然后利用尺规将它四等分.
(要求:写出已知、求作,利用尺规作图)
1
2
3
4
5
目录
CONTENTS
思考探究,获取新知
情景导入,初步认知
深化理解
课堂小结
课后作业
深化理解
习题
1、如图,已知⊿ABC内一点P到∠A的两边的距离相等,且PA=PB,则P点如何确定?
P
·
析:先作出∠BAC的平分线,
再作出线段AB的中垂线,
两线交点P就是所要确定的点.
∟
习题
2、如图,在⊿ABC中,BD是三角形的角平分线,BC=12cm,BA=8cm,点D到直线BC的距离等于4cm,求⊿ABC的面积.
深化理解
析:过D作DF垂直AB,垂足为F,
则,DF=DE=4
∴S⊿ABC = S⊿ABD+S⊿CBD
=(AB×DF+BC×DE)÷2
=40(cm2)
∟
F
习题
3、如图,BD是∠ABC的平分线,BA=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别为M,N. 试说明 PM=PN.
深化理解
析:先证明⊿ABD ≌⊿CBD(SAS),
得, ∠ADB =∠CDB,
根据角平分线的性质,得
PM = PN.
1
2
3
4
5
目录
CONTENTS
思考探究,获取新知
情景导入,初步认知
深化理解
课堂小结
课后作业
归纳1
角是轴对称图形,角平分线所在的直线是它的对称轴.
课堂小结
归纳2
角平分线上的点到这个角的两边的距离相等.
注意:这里的距离指的是“点到线的距离”
归纳3
掌握尺规作角平分线的方法与步骤.
1
2
3
目录
CONTENTS
思考探究,获取新知
情景导入,初步认知
深化理解
课堂小结
课后作业
4
5
课本 P127 习题5.5
第 2、3题
课后作业
下一节再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
