2021-2022学年北师大数学八年级下册1.1等腰三角形B 课后训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大数学八年级下册1.1等腰三角形B 课后训练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 439.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 19:39:31 | ||
图片预览



文档简介
北师大数学八年级下册第一章 三角形的证明 1.1等腰三角形 拓展提升(含答案)
姓名:___________班级:___________
一、单选题
1.等腰三角形的顶角为80°,则其底角的度数是( )
A.100° B.80° C.50° D.40°
2.下列命题中,是真命题的是( )
A.三角形的外角大于该三角形任意一个内角
B.如果点P(x,y)的坐标满足xy<0,那么点P一定在第二象限
C.如果两个直角三角形,有两组边分别相等,则这两个直角三角形全等
D.如果一个等腰三角形的一个内角为60°,那么这个三角形是等边三角形
3.在中,,于点D,若,,则的周长为( )
A.13 B.18 C.21 D.26
4.如图,已知为边的中点,在上,将沿着折叠,使点落在上的处.若,则等于( )
A.65 B. C. D.
5.等腰三角形的顶角是,则这个三角形的一个底角的大小是( )
A. B. C. D.
6.如图,在中,AB=AC,,点D是BC边上任意一点,过点D作DFAB交AC于点E,则∠FEA的度数是( )
A.60° B.50° C.35° D.30°
7.等腰三角形两边长分别为4和9,则该三角形第三边的长为( )
A.4 B.9 C.4或9 D.大于5且小于13
8.如图所示,∠AOB是一个钢架,且∠AOB=10°,为了使钢架更加牢固,需在内部添加一些钢管EF、FG、GH…添加钢管的长度都与OE相等,则最多能添加这样的钢管的根数为( )
A.15 B.9 C.8 D.7
9.如图,在纸片△ABC中,AC=6,∠A=30 ,∠C=90 ,将∠A沿DE折叠,使点A与点B重合,则折痕DE的长为( )
A.4 B.3 C.2 D.无法确定
10.如图,在△ABC中,以点B为圆心,AB为半径画弧交BC于点D,以点C为圆心,AC为半径画弧交BC于点E,连接AE,AD.设∠EAD=α,∠ACB=β,则∠B的度数为( )
A.α﹣ B.2α﹣β C.α+ D.3α﹣β
11.如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,若∠A=50°,则∠An﹣1AnBn﹣1的度数为( )
A. B. C. D.
12.如图1,在中,,于点.动点M从A点出发,沿折线方向运动,运动到点C停止.设点M的运动路程为x,的面积为y,y与x的函数图象如图2,则AC的长为( )
A.4 B.6 C.8 D.10
二、填空题
13.等腰三角形的一个内角为,则这个等腰三角形的一个底角的度数为_____.
14.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,若BC=4,则BD=_____.
15.如图,在平面直角坐标系中,∠AOB=30°,P(5,0),在OB上找一点M,在OA上找一点N,使△PMN周长最小,则此时△PMN的周长为 ___.
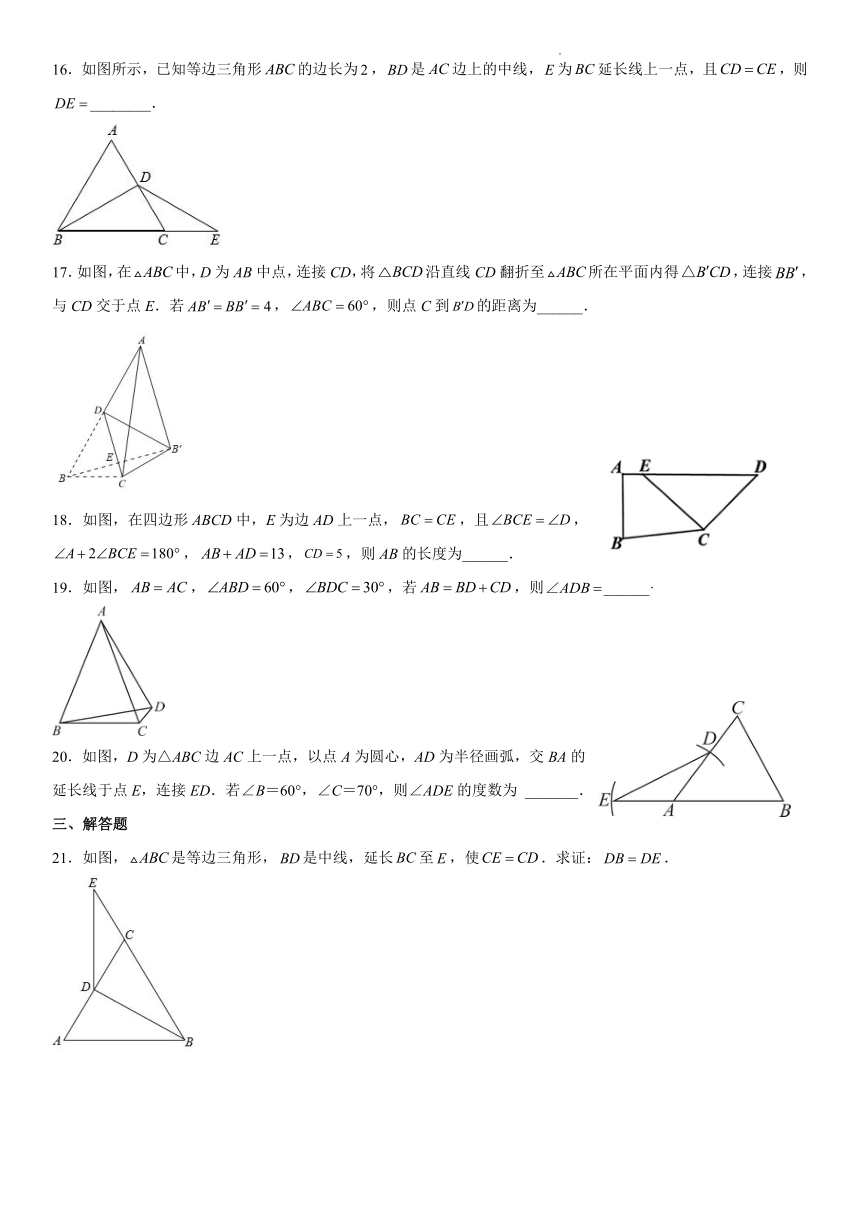
16.如图所示,已知等边三角形的边长为,是边上的中线,为延长线上一点,且,则________.
17.如图,在中,D为AB中点,连接CD,将沿直线CD翻折至所在平面内得,连接,与CD交于点E.若,,则点C到的距离为______.
18.如图,在四边形ABCD中,E为边AD上一点,,且,,,,则AB的长度为______.
19.如图,,,,若,则______·
20.如图,D为△ABC边AC上一点,以点A为圆心,AD为半径画弧,交BA的延长线于点E,连接ED.若∠B=60°,∠C=70°,则∠ADE的度数为 _______.
三、解答题
21.如图,是等边三角形,是中线,延长至,使.求证:.
22.已知:如图1,△ABC中,AB=AC,P是BC的中点,PD⊥AB,PE⊥AC,垂足分别是D、E,过点C做直线AB的垂线,垂足是F.
(1)若∠BAC=120°,求证:PD+PE=CF;
(2)若∠BAC=100°,(1)中的结论是否仍然成立?并说明理由.
(3)如图2,△ABC中,AB=AC,P是BC边上任意一点,PD⊥AB,PE⊥AC,垂足分别是D、E,已知△ABC的面积为15,AB=6,则PD+PE=_____.
23.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且BP=CD,∠APD=∠B.
(1)求证:AB=CP;
(2)若∠BAC=120°,则∠ADP= °.
24.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB//CE,AB=4,求DF的长.
25.如图,已知在Rt△ABC中,∠ACB=90°,AC=18,BC=36.点P从B点出发沿射线BC方向以每秒4个单位的速度向右运动.设点P的运动时间为t.连结AP.
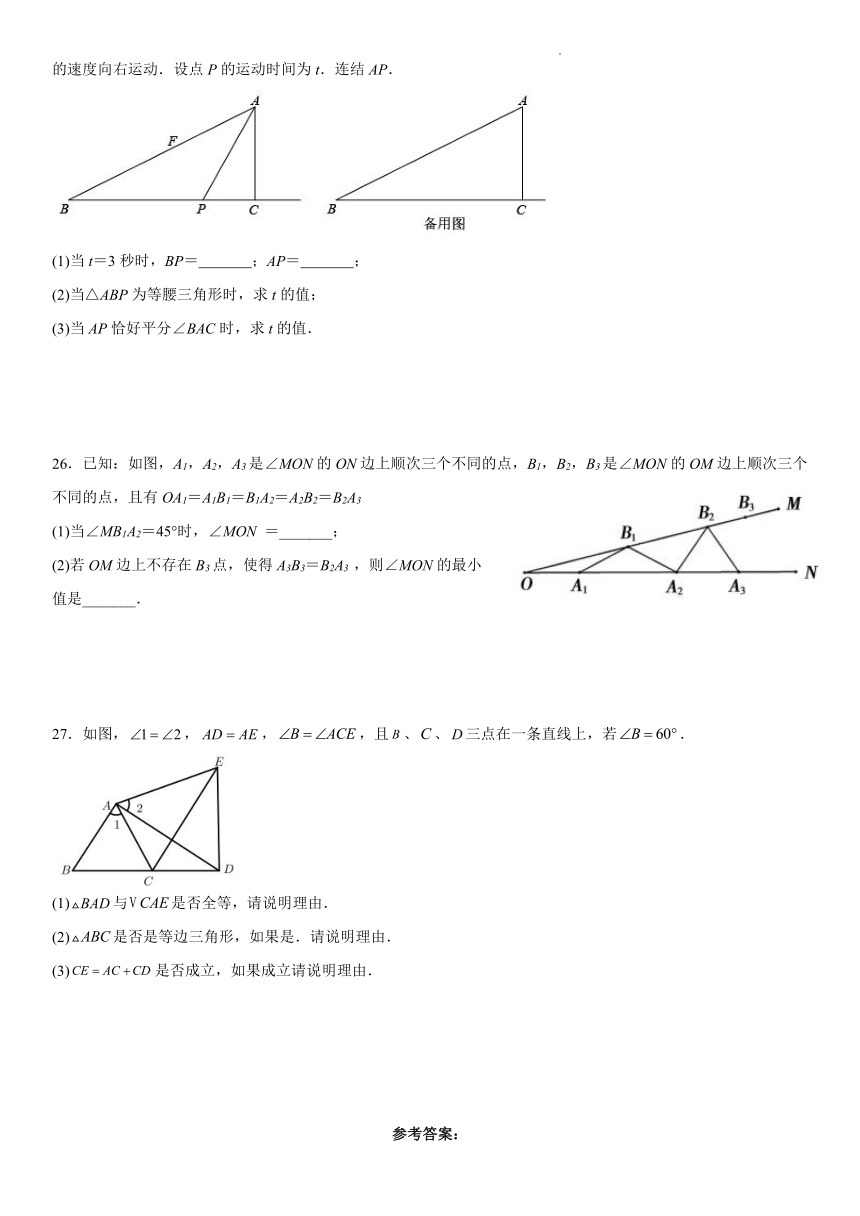
(1)当t=3秒时,BP= ;AP= ;
(2)当△ABP为等腰三角形时,求t的值;
(3)当AP恰好平分∠BAC时,求t的值.
26.已知:如图,A1,A2,A3是∠MON的ON边上顺次三个不同的点,B1,B2,B3是∠MON的OM边上顺次三个不同的点,且有OA1=A1B1=B1A2=A2B2=B2A3
(1)当∠MB1A2=45°时,∠MON =_______;
(2)若OM边上不存在B3点,使得A3B3=B2A3 ,则∠MON的最小值是_______.
27.如图,,,,且、、三点在一条直线上,若.
(1)与是否全等,请说明理由.
(2)是否是等边三角形,如果是.请说明理由.
(3)是否成立,如果成立请说明理由.
参考答案:
1.C 2.D 3.D 4.C 5.A 6.B 7.B 8.C 9.C 10.B 11.B 12.B
13.或
14.2
15.5
16.
17.3﹣
18.4
19.75°
20.
21.解:∵是等边三角形,
∴,.
∵是中线,
∴.
∵,
∴.
∵,
∴.
∴.
∴.
22.(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=120°,
∴∠ABC=∠ACB=(180°-120°)=30°,
在中,
∵∠ABC=30°,
∴PD=BP,
同理可证PE=CP,CF=BC,
∴PD+PE=BP+CP=(BP+CP)=BC=CF,
即PD+PF=CF;
(2)解:PD+PF=CF仍然成立,理由如下:
如图,连接AP,
∵S△ABP=AB·PD,S△ACP=AC·PE,
∴S△ABC=S△ABP+S△ACP=AB·PD+AC·PE,
∵AB=AC,
∴S△ABC=AB(PD+PE) ,
又∵S△ABC=AB·CF,
∴PD+PE=CF;
(3)如图,连接AP ,
∵S△ABC=S△ABP+S△ACP,PD⊥AB,PE⊥AC,
∴,
∵AB=AC,△ABC的面积为15,AB=6,
∴,
∴.
23.(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠APC=∠B+∠BAP=∠APD+∠CPD,且∠APD=∠B,
∴∠CPD=∠BAP,
在△ABP和△PCD中,
,
∴△ABP≌△PCD(AAS),
∴AB=CP;
(2)解:∵∠BAC=120°,∠B=∠C,
∴∠B=∠C=30°,
∵AB=AC,AB=PC,
∴PC=AC,
∴∠CAP=∠APC==75°,
由(1)知:△ABP≌△PCD,
∴AP=PD,
∴∠ADP=∠CAP=75°.
24.(1)证明:∵CB为∠ACE的平分线,
∴∠ACB=∠BCE.
在△ACB和△FCE中
,
∴△ACB≌△FCE.
∴AB=FE.
(2)∵AB∥CE,
∴∠B=∠BCE.
∵∠B=∠E,∠ACB=∠BCE,
∴∠E=∠BCE=∠ACB.
∴EF=FC.
∵AB=FE,AB=4,
∴FC=4.
∵ED⊥AC,
∴∠EDC=90°.
∴∠E+∠BCE+∠ACB=90°.
∴∠E=∠BCE=∠ACB=30°.
∴DF=CF=2.
25.(1)解:由题意得:BP=4t,
∴当t=3秒时,BP=4×3=12,
∵BC=36,
∴PC=BC﹣BP=36﹣12=24,
由勾股定理得:AP===30,
故答案为:12;30;
(2)在Rt△ABC中,AC=18,BC=36,
∴AB===18,
当BP=AB=18时,t=18÷4=;
当AP=AB时,BP=2BC=72,则t=72÷4=18;
当PA=PB=4t时,
在Rt△APC中,AP2=PC2+AC2,即(4t)2=(36﹣4t)2+182,
解得:t=,
综上所述,当△ABP为等腰三角形时,t=或18或;
(3)如图,过点P作PF⊥AB于F,
∵AP平分∠BAC,PF⊥AB,∠ACB=90°,
∴PC=PF=36﹣4t,
在Rt△APF和Rt△APC中,
,
∴Rt△APF≌Rt△APC(HL),
∴AF=AC=18,
∴BF=18﹣18,
在Rt△BPF中,BP2=PF2+BF2,即(4t)2=(18﹣18)2+(36﹣4t)2,
解得:t=,即AP恰好平分∠BAC时,t=.
26.(1)解:∵OA1=A1B1=B1A2=A2B2=B2A3
∴,,
∵,,
∴,
∴∠MON=15°;
故答案为:15°;
(2)解:∵OM边上不存在B3点,使得A3B3=B2A3 ,
∴OM边上不存在B3点,使得,
∴ ,
同理可求出 ,
∴,
∴,
∴,
27.(1)解:与全等;
理由如下:
∵,
∴,即,
在与中,
,
∴;
(2)解:∵,
∴,
又∵,
∴是等边三角形;
(3)解:成立,
理由如下:
∵,
∴,
∵是等边三角形,
∴,
∴,即.
答案第1页,共2页
姓名:___________班级:___________
一、单选题
1.等腰三角形的顶角为80°,则其底角的度数是( )
A.100° B.80° C.50° D.40°
2.下列命题中,是真命题的是( )
A.三角形的外角大于该三角形任意一个内角
B.如果点P(x,y)的坐标满足xy<0,那么点P一定在第二象限
C.如果两个直角三角形,有两组边分别相等,则这两个直角三角形全等
D.如果一个等腰三角形的一个内角为60°,那么这个三角形是等边三角形
3.在中,,于点D,若,,则的周长为( )
A.13 B.18 C.21 D.26
4.如图,已知为边的中点,在上,将沿着折叠,使点落在上的处.若,则等于( )
A.65 B. C. D.
5.等腰三角形的顶角是,则这个三角形的一个底角的大小是( )
A. B. C. D.
6.如图,在中,AB=AC,,点D是BC边上任意一点,过点D作DFAB交AC于点E,则∠FEA的度数是( )
A.60° B.50° C.35° D.30°
7.等腰三角形两边长分别为4和9,则该三角形第三边的长为( )
A.4 B.9 C.4或9 D.大于5且小于13
8.如图所示,∠AOB是一个钢架,且∠AOB=10°,为了使钢架更加牢固,需在内部添加一些钢管EF、FG、GH…添加钢管的长度都与OE相等,则最多能添加这样的钢管的根数为( )
A.15 B.9 C.8 D.7
9.如图,在纸片△ABC中,AC=6,∠A=30 ,∠C=90 ,将∠A沿DE折叠,使点A与点B重合,则折痕DE的长为( )
A.4 B.3 C.2 D.无法确定
10.如图,在△ABC中,以点B为圆心,AB为半径画弧交BC于点D,以点C为圆心,AC为半径画弧交BC于点E,连接AE,AD.设∠EAD=α,∠ACB=β,则∠B的度数为( )
A.α﹣ B.2α﹣β C.α+ D.3α﹣β
11.如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,若∠A=50°,则∠An﹣1AnBn﹣1的度数为( )
A. B. C. D.
12.如图1,在中,,于点.动点M从A点出发,沿折线方向运动,运动到点C停止.设点M的运动路程为x,的面积为y,y与x的函数图象如图2,则AC的长为( )
A.4 B.6 C.8 D.10
二、填空题
13.等腰三角形的一个内角为,则这个等腰三角形的一个底角的度数为_____.
14.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,若BC=4,则BD=_____.
15.如图,在平面直角坐标系中,∠AOB=30°,P(5,0),在OB上找一点M,在OA上找一点N,使△PMN周长最小,则此时△PMN的周长为 ___.
16.如图所示,已知等边三角形的边长为,是边上的中线,为延长线上一点,且,则________.
17.如图,在中,D为AB中点,连接CD,将沿直线CD翻折至所在平面内得,连接,与CD交于点E.若,,则点C到的距离为______.
18.如图,在四边形ABCD中,E为边AD上一点,,且,,,,则AB的长度为______.
19.如图,,,,若,则______·
20.如图,D为△ABC边AC上一点,以点A为圆心,AD为半径画弧,交BA的延长线于点E,连接ED.若∠B=60°,∠C=70°,则∠ADE的度数为 _______.
三、解答题
21.如图,是等边三角形,是中线,延长至,使.求证:.
22.已知:如图1,△ABC中,AB=AC,P是BC的中点,PD⊥AB,PE⊥AC,垂足分别是D、E,过点C做直线AB的垂线,垂足是F.
(1)若∠BAC=120°,求证:PD+PE=CF;
(2)若∠BAC=100°,(1)中的结论是否仍然成立?并说明理由.
(3)如图2,△ABC中,AB=AC,P是BC边上任意一点,PD⊥AB,PE⊥AC,垂足分别是D、E,已知△ABC的面积为15,AB=6,则PD+PE=_____.
23.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且BP=CD,∠APD=∠B.
(1)求证:AB=CP;
(2)若∠BAC=120°,则∠ADP= °.
24.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC交于点D.
(1)求证:AB=FE;
(2)若ED⊥AC,AB//CE,AB=4,求DF的长.
25.如图,已知在Rt△ABC中,∠ACB=90°,AC=18,BC=36.点P从B点出发沿射线BC方向以每秒4个单位的速度向右运动.设点P的运动时间为t.连结AP.
(1)当t=3秒时,BP= ;AP= ;
(2)当△ABP为等腰三角形时,求t的值;
(3)当AP恰好平分∠BAC时,求t的值.
26.已知:如图,A1,A2,A3是∠MON的ON边上顺次三个不同的点,B1,B2,B3是∠MON的OM边上顺次三个不同的点,且有OA1=A1B1=B1A2=A2B2=B2A3
(1)当∠MB1A2=45°时,∠MON =_______;
(2)若OM边上不存在B3点,使得A3B3=B2A3 ,则∠MON的最小值是_______.
27.如图,,,,且、、三点在一条直线上,若.
(1)与是否全等,请说明理由.
(2)是否是等边三角形,如果是.请说明理由.
(3)是否成立,如果成立请说明理由.
参考答案:
1.C 2.D 3.D 4.C 5.A 6.B 7.B 8.C 9.C 10.B 11.B 12.B
13.或
14.2
15.5
16.
17.3﹣
18.4
19.75°
20.
21.解:∵是等边三角形,
∴,.
∵是中线,
∴.
∵,
∴.
∵,
∴.
∴.
∴.
22.(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=120°,
∴∠ABC=∠ACB=(180°-120°)=30°,
在中,
∵∠ABC=30°,
∴PD=BP,
同理可证PE=CP,CF=BC,
∴PD+PE=BP+CP=(BP+CP)=BC=CF,
即PD+PF=CF;
(2)解:PD+PF=CF仍然成立,理由如下:
如图,连接AP,
∵S△ABP=AB·PD,S△ACP=AC·PE,
∴S△ABC=S△ABP+S△ACP=AB·PD+AC·PE,
∵AB=AC,
∴S△ABC=AB(PD+PE) ,
又∵S△ABC=AB·CF,
∴PD+PE=CF;
(3)如图,连接AP ,
∵S△ABC=S△ABP+S△ACP,PD⊥AB,PE⊥AC,
∴,
∵AB=AC,△ABC的面积为15,AB=6,
∴,
∴.
23.(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠APC=∠B+∠BAP=∠APD+∠CPD,且∠APD=∠B,
∴∠CPD=∠BAP,
在△ABP和△PCD中,
,
∴△ABP≌△PCD(AAS),
∴AB=CP;
(2)解:∵∠BAC=120°,∠B=∠C,
∴∠B=∠C=30°,
∵AB=AC,AB=PC,
∴PC=AC,
∴∠CAP=∠APC==75°,
由(1)知:△ABP≌△PCD,
∴AP=PD,
∴∠ADP=∠CAP=75°.
24.(1)证明:∵CB为∠ACE的平分线,
∴∠ACB=∠BCE.
在△ACB和△FCE中
,
∴△ACB≌△FCE.
∴AB=FE.
(2)∵AB∥CE,
∴∠B=∠BCE.
∵∠B=∠E,∠ACB=∠BCE,
∴∠E=∠BCE=∠ACB.
∴EF=FC.
∵AB=FE,AB=4,
∴FC=4.
∵ED⊥AC,
∴∠EDC=90°.
∴∠E+∠BCE+∠ACB=90°.
∴∠E=∠BCE=∠ACB=30°.
∴DF=CF=2.
25.(1)解:由题意得:BP=4t,
∴当t=3秒时,BP=4×3=12,
∵BC=36,
∴PC=BC﹣BP=36﹣12=24,
由勾股定理得:AP===30,
故答案为:12;30;
(2)在Rt△ABC中,AC=18,BC=36,
∴AB===18,
当BP=AB=18时,t=18÷4=;
当AP=AB时,BP=2BC=72,则t=72÷4=18;
当PA=PB=4t时,
在Rt△APC中,AP2=PC2+AC2,即(4t)2=(36﹣4t)2+182,
解得:t=,
综上所述,当△ABP为等腰三角形时,t=或18或;
(3)如图,过点P作PF⊥AB于F,
∵AP平分∠BAC,PF⊥AB,∠ACB=90°,
∴PC=PF=36﹣4t,
在Rt△APF和Rt△APC中,
,
∴Rt△APF≌Rt△APC(HL),
∴AF=AC=18,
∴BF=18﹣18,
在Rt△BPF中,BP2=PF2+BF2,即(4t)2=(18﹣18)2+(36﹣4t)2,
解得:t=,即AP恰好平分∠BAC时,t=.
26.(1)解:∵OA1=A1B1=B1A2=A2B2=B2A3
∴,,
∵,,
∴,
∴∠MON=15°;
故答案为:15°;
(2)解:∵OM边上不存在B3点,使得A3B3=B2A3 ,
∴OM边上不存在B3点,使得,
∴ ,
同理可求出 ,
∴,
∴,
∴,
27.(1)解:与全等;
理由如下:
∵,
∴,即,
在与中,
,
∴;
(2)解:∵,
∴,
又∵,
∴是等边三角形;
(3)解:成立,
理由如下:
∵,
∴,
∵是等边三角形,
∴,
∴,即.
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
