第5章 生活中的轴对称 单元测试卷(七)
文档属性
| 名称 | 第5章 生活中的轴对称 单元测试卷(七) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 14:14:30 | ||
图片预览



文档简介
第5章《生活中的轴对称》单元测试
(本检测题满分:100分 时间:90分钟)
一、选择题(每小题3分,共30分)
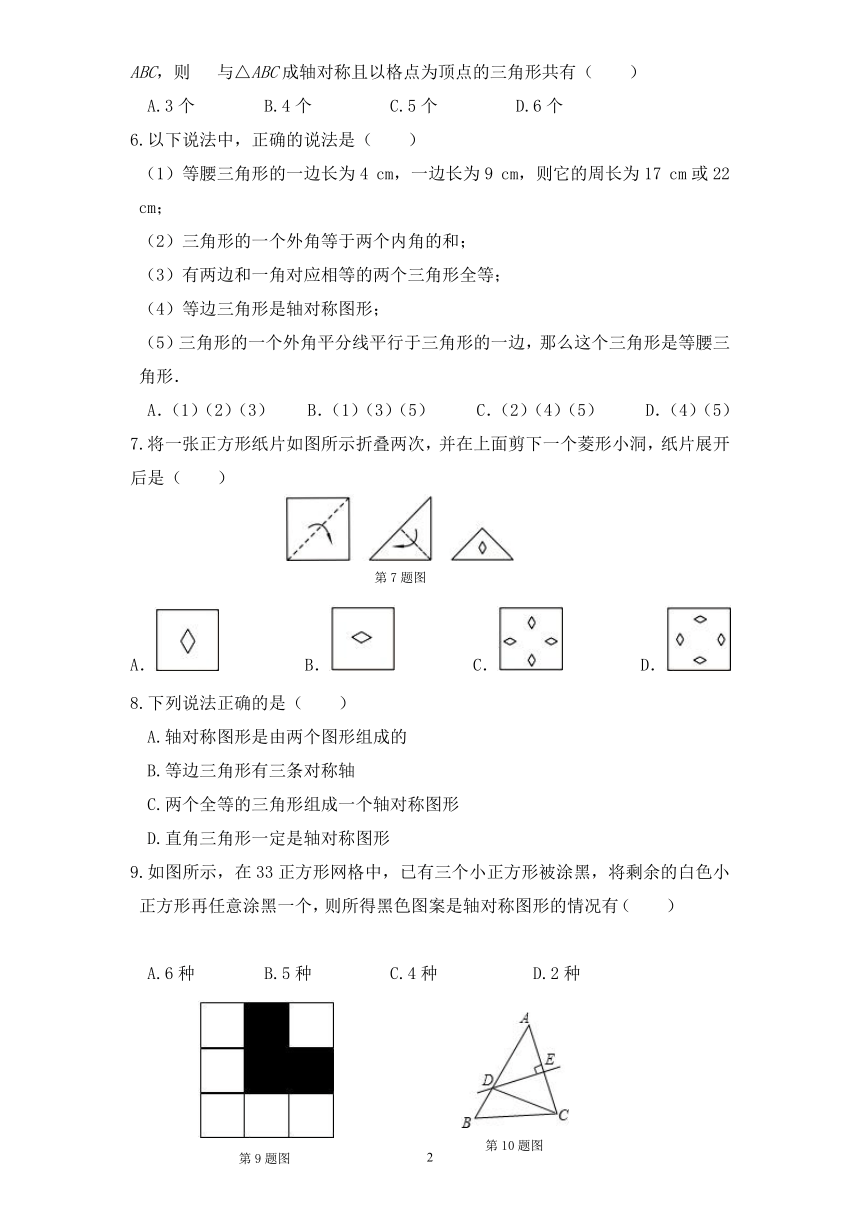
1.下列图中不是轴对称图形的是( )
2.如图的方格纸中,左边图形到右边图形的变换是( )
A.向右平移7个单位长度
B.以AB的垂直平分线为对称轴作轴对称变换,再以AB所在直线为对称轴作轴对称变换
C.绕AB的中点旋转180°,再以AB所在直线为对称轴作轴对称变换
D.以AB所在直线为对称轴作轴对称变换,再向右平移7个单位长度
3.如图所示,△与△关于直线对称,则∠等于( )
A. B.
C. D.
4.下列说法正确的是( )
A.如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形
B.任何一个图形都有对称轴,有的图形不止一条对称轴
C.平面上两个大小、形状完全一样的图形一定关于某直线对称
D.如果△ABC和△EFG成轴对称,那么它们的面积一定相等
5.如图所示,在22的方格纸中有一个以格点为顶点的△ABC,则 与△ABC成轴对称且以格点为顶点的三角形共有( )
A.3个 B.4个 C.5个 D.6个
6.以下说法中,正确的说法是( )
(1)等腰三角形的一边长为4 cm,一边长为9 cm,则它的周长为17 cm或22 cm;
(2)三角形的一个外角等于两个内角的和;
(3)有两边和一角对应相等的两个三角形全等;
(4)等边三角形是轴对称图形;
(5)三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A.(1)(2)(3) B.(1)(3)(5) C.(2)(4)(5) D.(4)(5)
7.将一张正方形纸片如图所示折叠两次,并在上面剪下一个菱形小洞,纸片展开后是( )
A. B. C. D.
8.下列说法正确的是( )
A.轴对称图形是由两个图形组成的
B.等边三角形有三条对称轴
C.两个全等的三角形组成一个轴对称图形
D.直角三角形一定是轴对称图形
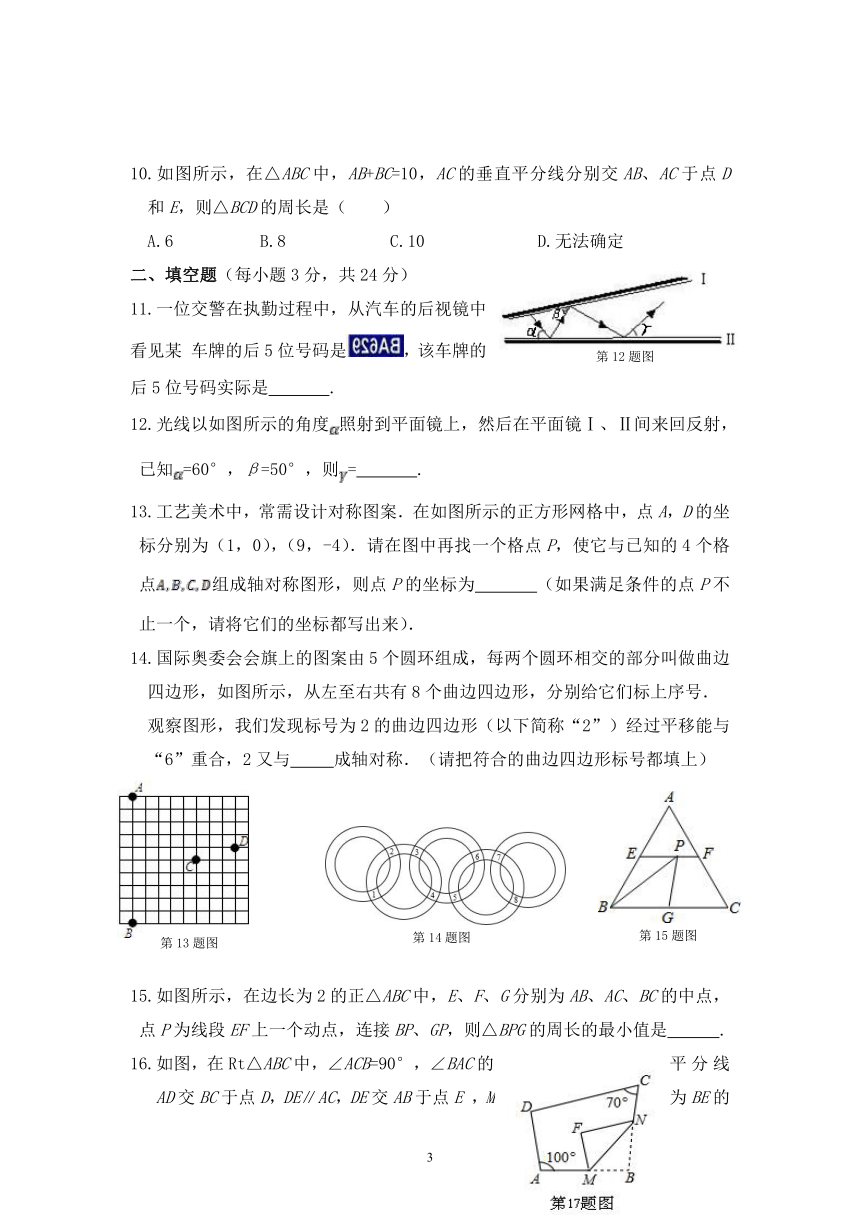
9.如图所示,在33正方形网格中,已有三个小正方形被涂黑,将剩余的白色小正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有( ) 来源:http://www./tiku/
A.6种 B.5种 C.4种 D.2种
10.如图所示,在△ABC中,AB+BC=10,AC的垂直平分线分别交AB、AC于点D和E,则△BCD的周长是( )
A.6 B.8 C.10 D.无法确定
二、填空题(每小题3分,共24分)
11.一位交警在执勤过程中,从汽车的后视镜中看见某 车牌的后5位号码是,该车牌的后5位号码实际是 .
12.光线以如图所示的角度照射到平面镜上,然后在平面镜Ⅰ、Ⅱ间来回反射,已知=60°,β=50°,则= .
13.工艺美术中,常需设计对称图案.在如图所示的正方形网格中,点A,D的坐标分别为(1,0),(9,-4).请在图中再找一个格点P,使它与已知的4个格点组成轴对称图形,则点P的坐标为 (如果满足条件的点P不止一个,请将它们的坐标都写出来).
14.国际奥委会会旗上的图案由5个圆环组成,每两个圆环相交的部分叫做曲边四边形,如图所示,从左至右共有8个曲边四边形,分别给它们标上序号.
观察图形,我们发现标号为2的曲边四边形(以下简称“2”)经过平移能与“6”重合,2又与 成轴对称.(请把符合的曲边四边形标号都填上)
15.如图所示,在边长为2的正△ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是 .
16.如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AD交BC于点D,DE∥AC,DE交AB于点E ,M为BE的中点,连接DM. 在不添加任何辅助线和字母的情况下,图中的等腰三角形是 .(写出一个即可)
17.如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B= .
18.在平面直角坐标系中,点P(,3)与Q()关于y轴对称,则= .
三、解答题(共46分) 来源:http://www./tiku/
19.(6分)将16个相同的小正方形拼成正方形网格,并将其中的两个小正方形涂成黑色,请你用两种不同的方法分别在图甲、图乙中再将两个空白的小正方形涂黑,使它成为轴对称图形.
20.(6分)如图所示,△ABC是等边三角形,∠1=∠2=∠3,
求∠BEC的度数.
21.(6分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于轴对称的△A′B′C′;
(3)写出点B′的坐标.
22.(6分)公园内有一块三角形空地(如图所示),现要将它分割成三块,种植三种不同的花卉,为了美观,要求每块都是轴对称图形,请你在图中画出分割线,保留必要的画图痕迹.
23.(6分)如图所示,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
24.(8分)如图所示,等边△ABC中,D为AC边的中点,E为BC延长线上一点,CE=CD,DM⊥BC于M,求证:M是BE的中点. 来源:http://www./tiku/
25.(8分)如图所示,∠内有一点,在射线上找出一点,在射线上找出一点,使最短.
参考答案
1.C 解析:由轴对称的性质可知A、B、D都能找到对称轴,而C找不到对称轴,故选C.
2.D 解析:观察可得:要使左边图形变化到右边图形,首先以AB为对称轴作轴对称变换,再向右平移7个单位长度.故选D.
3.D 解析:因为 △与△关于直线对称,
所以所以.
4.D 解析:A.图形甲和图形乙关于直线MN对称,图形甲不一定是轴对称图形,
错误;
B.有的图形没有对称轴,错误;
C.平面上两个大小、形状完全一样的图形不一定关于某直线对称,与摆放位置有关,错误;
D.如果△ABC和△EFG成轴对称,那么它们全等,故其面积一定相等,正确.故选D.
5. C 解析:与△ABC成轴对称且以格点为顶点的三角形有
△ABG、△CDF、△AEF、△DBH、△BCG,共5个,故选C.
6.D 解析:(1)等腰三角形的一边长为4 cm,一边长为9 cm,则三边长为9 cm,9 cm,4 cm,或4 cm,4 cm,9 cm,因为4+4<9,则它的周长只能是22 cm,故(1)错误;
(2)三角形的一个外角等于与它不相邻的两个内角的和,故(2)错误;
(3)有两边和一角对应相等的两个三角形全等错误,必须是夹角;
(4)等边三角形是轴对称图形,故(4)正确;
(5)三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形,正确.
如图所示:∵ AD∥BC,∴ ∠1=∠B,∠2=∠C.
∵ AD是∠A外角平分线,∴ ∠1=∠2,
∴ ∠B =∠C,∴ AB =AC.
即△ABC是等腰三角形.故选D.
7.C 解析:当正方形纸片两次沿对角线对折成为一直角三角形时,在垂直于斜边的位置上剪菱形,则直角顶点处完好,即原正方形中间无损,且菱形关于对角线对称.故选C.
8.B 解析:A.轴对称图形是指1个图形,故错误;
B.等边三角形有三条对称轴,即三条中线所在直线,故正确;
C.两个全等的三角形不一定组成一个轴对称图形,故错误;
D.直角三角形不一定是轴对称图形,只有等腰直角三角形是轴对称图形,故错误.
故选B.
9.C 解析:根据题意,涂黑每一个格都会出现一种等可能情况,共出现6种等可能情况,
而当涂黑左上角和右下角的小正方形时,不会是轴对称图形,其余的4种情况均可以.
故选C.
10.C 解析:∵ DE是AC的垂直平分线,∴ AD=DC,
△BCD的周长=BC+BD+DC=BC+BD+AD=10.故选C.
11.BA629 解析:关于镜面对称,也可以看成是关于某条直线对称,关于某条直线对称的后5位号码是BA629.
12.40° 解析:=180°-[60°+(180°-100°)]=40°.
13.(9,-6)(2,-3) 解析:∵ 点A的坐标为(1,0),
∴ 坐标原点是点A左边一个单位的格点.
∵ 点C在线段AB的垂直平分线上,
∴ 对称轴是线段AB的垂直平分线,
∴ 点P是点D关于对称轴的对称点.
∵ 点D的坐标是(9,-4),
∴ P(9,-6).AB=BD,以AD的垂直平分线为对称轴,P′与C关于AD的垂直平分线对称.
∵ C点的坐标为(6,-5),∴ P′(2,-3).
14.1,3,7 解析:根据轴对称图形的定义可知:标号为2的曲边四边形与标号为1,3,7的曲边四边形成轴对称.
15.3 解析:要使△PBG的周长最小,而BG=1一定,只要使BP+PG最小即可.
连接AG交EF于点M.
∵ △ABC是等边三角形,E、F、G分别为AB、AC、BC的中点,
∴ AG⊥BC,EF∥BC,
∴ AG⊥EF,AM=MG,
∴ 点A、G关于EF对称,
∴ 点P与点E重合时,BP+PG最小,
即△PBG的周长最小,
最小值是:PB +PG +BG =AE +BE +BG =AB +BG =2+1=3.
16.△MBD、△MDE、△EAD 解析:由∠ACB=90°,DE∥AC,得∠EDC=90°,又M为BE的中点,得MB=MD=ME,∴△MBD和△MDE是等腰三角形.
∵ ∠BAC的平分线AD交BC于点D,DE∥AC,∴ ∠EDA=∠EAD=∠DAC,
∴ △EAD是等腰三角形.
17. 95° 解析:∵ MF∥AD,FN∥DC,∴ ∠BMF=∠A=100°,∠BNF=∠C=70°.
∵ △BMN沿MN翻折得△FMN,∴ ∠BMN= ∠BMF=×100°=50°,∠BNM=∠BNF=×70°=35°,
在△BMN中,∠B=180°-(∠BMN+∠BNM)=180°-(50°+35°)=180°-85°=95°.
18.1 解析:∵ 关于y轴对称的点纵坐标相同,横坐标互为相反数,
又∵ 点P(2,3)与Q(4,5)关于y轴对称,∴
解得∴()2 012=1.
19.分析:根据轴对称图形的性质,分别在图甲、图乙中再将两个空白的小正方形涂黑,使它成为轴对称图形即可.
解:如图所示.(答案不唯一)
20.解:∵ △ABC是等边三角形,
∴ AB=BC=CA,∠ABC=∠BCA=∠CAB=60°.
又∵ ∠1=∠2=∠3,
∴ ∠BAC-∠1=∠ABC-∠2=∠BCA-∠3,
即∠CAF=∠ABD=∠BCE.
在△ABD和△BCE和△CAF中,
∴ △ABD≌△BCE≌△CAF(ASA).
∴ AD=BE=CF,BD=CE=AF.∴ AD-AF=BE-BD=CF-CE,
即FD=DE=EF.
∴ △DEF是等边三角形.
∴ ∠FED=60°.
∴ ∠BEC=180°-∠FED=180°-60°=120°.
21.分析:(1)易得y轴在C的右边一个单位,轴在C的下方3个单位;
(2)作出A,B,C三点关于y轴对称的三点,顺次连接即可;
(3)根据所在象限及与坐标轴的距离可得相应坐标.
解:(1)(2)如图所示;
(3)点B′的坐标为(2,1).
22.解:如图,分别作AB、BC的垂直平分线,相交于点P,
沿PA、PB、PC进行分割,得到的△PAB、△PBC、△PAC都是等腰三角形,都是轴对称图形.
23. (1)证明:∵ ABCD是长方形,∴ AD=BC,∠D=∠B=90°.
根据折叠的性质,有GC=AD,∠G=∠D,∴ GC=BC,∠G=∠B.
又∠GCF+∠ECF=90°,∠BCE+∠ECF=90°,∴ ∠GCF=∠BCE.∴ △FGC≌△EBC(ASA).
(2)解:由(1)知,四边形ECGF的面积=四边形EADF的面积=四边形EBCF的面积=矩形ABCD的面积的一半.
∵ AB=8,AD=4,∴ 矩形ABCD的面积=8×4=32,∴ 阴影部分的面积=16.
24.分析:欲证M是BE的中点,已知DM⊥BC,因此只需证DB=DE,即证∠DBE=∠E,根据BD是等边△ABC的中线可知∠DBC=30°,因此只需证∠E=30°.
证明:连接BD,
∵ △ABC是等边三角形,∴ ∠ABC=∠ACB=60°.
∵ CD=CE,∴ ∠CDE=∠E=30°.
∵ BD是AC边上的中线,∴ BD平分∠ABC,即∠DBC=30°,
∴ ∠DBE=∠E.∴ DB=DE.又∵ DM⊥BE,
∴ DM是BE边上的中线,即M是BE的中点.
25.解:如图所示,分别以直线、为对称轴,作点的对应点和,连接,交于点,交于点,则最短,即.
第3题图
第2题图
第5题图
第7题图
第10题图
第9题图
第12题图
第13题图
第15题图
第14题图
第16题图
第20题图
第21题图
第22题图
第25题图
第5题答图
第6题答图
第15题答图
第19题答图
第22题答图
第21题答图
O
P
M
N
第25题答图
Y
X
PAGE
1
(本检测题满分:100分 时间:90分钟)
一、选择题(每小题3分,共30分)
1.下列图中不是轴对称图形的是( )
2.如图的方格纸中,左边图形到右边图形的变换是( )
A.向右平移7个单位长度
B.以AB的垂直平分线为对称轴作轴对称变换,再以AB所在直线为对称轴作轴对称变换
C.绕AB的中点旋转180°,再以AB所在直线为对称轴作轴对称变换
D.以AB所在直线为对称轴作轴对称变换,再向右平移7个单位长度
3.如图所示,△与△关于直线对称,则∠等于( )
A. B.
C. D.
4.下列说法正确的是( )
A.如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形
B.任何一个图形都有对称轴,有的图形不止一条对称轴
C.平面上两个大小、形状完全一样的图形一定关于某直线对称
D.如果△ABC和△EFG成轴对称,那么它们的面积一定相等
5.如图所示,在22的方格纸中有一个以格点为顶点的△ABC,则 与△ABC成轴对称且以格点为顶点的三角形共有( )
A.3个 B.4个 C.5个 D.6个
6.以下说法中,正确的说法是( )
(1)等腰三角形的一边长为4 cm,一边长为9 cm,则它的周长为17 cm或22 cm;
(2)三角形的一个外角等于两个内角的和;
(3)有两边和一角对应相等的两个三角形全等;
(4)等边三角形是轴对称图形;
(5)三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A.(1)(2)(3) B.(1)(3)(5) C.(2)(4)(5) D.(4)(5)
7.将一张正方形纸片如图所示折叠两次,并在上面剪下一个菱形小洞,纸片展开后是( )
A. B. C. D.
8.下列说法正确的是( )
A.轴对称图形是由两个图形组成的
B.等边三角形有三条对称轴
C.两个全等的三角形组成一个轴对称图形
D.直角三角形一定是轴对称图形
9.如图所示,在33正方形网格中,已有三个小正方形被涂黑,将剩余的白色小正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有( ) 来源:http://www./tiku/
A.6种 B.5种 C.4种 D.2种
10.如图所示,在△ABC中,AB+BC=10,AC的垂直平分线分别交AB、AC于点D和E,则△BCD的周长是( )
A.6 B.8 C.10 D.无法确定
二、填空题(每小题3分,共24分)
11.一位交警在执勤过程中,从汽车的后视镜中看见某 车牌的后5位号码是,该车牌的后5位号码实际是 .
12.光线以如图所示的角度照射到平面镜上,然后在平面镜Ⅰ、Ⅱ间来回反射,已知=60°,β=50°,则= .
13.工艺美术中,常需设计对称图案.在如图所示的正方形网格中,点A,D的坐标分别为(1,0),(9,-4).请在图中再找一个格点P,使它与已知的4个格点组成轴对称图形,则点P的坐标为 (如果满足条件的点P不止一个,请将它们的坐标都写出来).
14.国际奥委会会旗上的图案由5个圆环组成,每两个圆环相交的部分叫做曲边四边形,如图所示,从左至右共有8个曲边四边形,分别给它们标上序号.
观察图形,我们发现标号为2的曲边四边形(以下简称“2”)经过平移能与“6”重合,2又与 成轴对称.(请把符合的曲边四边形标号都填上)
15.如图所示,在边长为2的正△ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是 .
16.如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AD交BC于点D,DE∥AC,DE交AB于点E ,M为BE的中点,连接DM. 在不添加任何辅助线和字母的情况下,图中的等腰三角形是 .(写出一个即可)
17.如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B= .
18.在平面直角坐标系中,点P(,3)与Q()关于y轴对称,则= .
三、解答题(共46分) 来源:http://www./tiku/
19.(6分)将16个相同的小正方形拼成正方形网格,并将其中的两个小正方形涂成黑色,请你用两种不同的方法分别在图甲、图乙中再将两个空白的小正方形涂黑,使它成为轴对称图形.
20.(6分)如图所示,△ABC是等边三角形,∠1=∠2=∠3,
求∠BEC的度数.
21.(6分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于轴对称的△A′B′C′;
(3)写出点B′的坐标.
22.(6分)公园内有一块三角形空地(如图所示),现要将它分割成三块,种植三种不同的花卉,为了美观,要求每块都是轴对称图形,请你在图中画出分割线,保留必要的画图痕迹.
23.(6分)如图所示,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
24.(8分)如图所示,等边△ABC中,D为AC边的中点,E为BC延长线上一点,CE=CD,DM⊥BC于M,求证:M是BE的中点. 来源:http://www./tiku/
25.(8分)如图所示,∠内有一点,在射线上找出一点,在射线上找出一点,使最短.
参考答案
1.C 解析:由轴对称的性质可知A、B、D都能找到对称轴,而C找不到对称轴,故选C.
2.D 解析:观察可得:要使左边图形变化到右边图形,首先以AB为对称轴作轴对称变换,再向右平移7个单位长度.故选D.
3.D 解析:因为 △与△关于直线对称,
所以所以.
4.D 解析:A.图形甲和图形乙关于直线MN对称,图形甲不一定是轴对称图形,
错误;
B.有的图形没有对称轴,错误;
C.平面上两个大小、形状完全一样的图形不一定关于某直线对称,与摆放位置有关,错误;
D.如果△ABC和△EFG成轴对称,那么它们全等,故其面积一定相等,正确.故选D.
5. C 解析:与△ABC成轴对称且以格点为顶点的三角形有
△ABG、△CDF、△AEF、△DBH、△BCG,共5个,故选C.
6.D 解析:(1)等腰三角形的一边长为4 cm,一边长为9 cm,则三边长为9 cm,9 cm,4 cm,或4 cm,4 cm,9 cm,因为4+4<9,则它的周长只能是22 cm,故(1)错误;
(2)三角形的一个外角等于与它不相邻的两个内角的和,故(2)错误;
(3)有两边和一角对应相等的两个三角形全等错误,必须是夹角;
(4)等边三角形是轴对称图形,故(4)正确;
(5)三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形,正确.
如图所示:∵ AD∥BC,∴ ∠1=∠B,∠2=∠C.
∵ AD是∠A外角平分线,∴ ∠1=∠2,
∴ ∠B =∠C,∴ AB =AC.
即△ABC是等腰三角形.故选D.
7.C 解析:当正方形纸片两次沿对角线对折成为一直角三角形时,在垂直于斜边的位置上剪菱形,则直角顶点处完好,即原正方形中间无损,且菱形关于对角线对称.故选C.
8.B 解析:A.轴对称图形是指1个图形,故错误;
B.等边三角形有三条对称轴,即三条中线所在直线,故正确;
C.两个全等的三角形不一定组成一个轴对称图形,故错误;
D.直角三角形不一定是轴对称图形,只有等腰直角三角形是轴对称图形,故错误.
故选B.
9.C 解析:根据题意,涂黑每一个格都会出现一种等可能情况,共出现6种等可能情况,
而当涂黑左上角和右下角的小正方形时,不会是轴对称图形,其余的4种情况均可以.
故选C.
10.C 解析:∵ DE是AC的垂直平分线,∴ AD=DC,
△BCD的周长=BC+BD+DC=BC+BD+AD=10.故选C.
11.BA629 解析:关于镜面对称,也可以看成是关于某条直线对称,关于某条直线对称的后5位号码是BA629.
12.40° 解析:=180°-[60°+(180°-100°)]=40°.
13.(9,-6)(2,-3) 解析:∵ 点A的坐标为(1,0),
∴ 坐标原点是点A左边一个单位的格点.
∵ 点C在线段AB的垂直平分线上,
∴ 对称轴是线段AB的垂直平分线,
∴ 点P是点D关于对称轴的对称点.
∵ 点D的坐标是(9,-4),
∴ P(9,-6).AB=BD,以AD的垂直平分线为对称轴,P′与C关于AD的垂直平分线对称.
∵ C点的坐标为(6,-5),∴ P′(2,-3).
14.1,3,7 解析:根据轴对称图形的定义可知:标号为2的曲边四边形与标号为1,3,7的曲边四边形成轴对称.
15.3 解析:要使△PBG的周长最小,而BG=1一定,只要使BP+PG最小即可.
连接AG交EF于点M.
∵ △ABC是等边三角形,E、F、G分别为AB、AC、BC的中点,
∴ AG⊥BC,EF∥BC,
∴ AG⊥EF,AM=MG,
∴ 点A、G关于EF对称,
∴ 点P与点E重合时,BP+PG最小,
即△PBG的周长最小,
最小值是:PB +PG +BG =AE +BE +BG =AB +BG =2+1=3.
16.△MBD、△MDE、△EAD 解析:由∠ACB=90°,DE∥AC,得∠EDC=90°,又M为BE的中点,得MB=MD=ME,∴△MBD和△MDE是等腰三角形.
∵ ∠BAC的平分线AD交BC于点D,DE∥AC,∴ ∠EDA=∠EAD=∠DAC,
∴ △EAD是等腰三角形.
17. 95° 解析:∵ MF∥AD,FN∥DC,∴ ∠BMF=∠A=100°,∠BNF=∠C=70°.
∵ △BMN沿MN翻折得△FMN,∴ ∠BMN= ∠BMF=×100°=50°,∠BNM=∠BNF=×70°=35°,
在△BMN中,∠B=180°-(∠BMN+∠BNM)=180°-(50°+35°)=180°-85°=95°.
18.1 解析:∵ 关于y轴对称的点纵坐标相同,横坐标互为相反数,
又∵ 点P(2,3)与Q(4,5)关于y轴对称,∴
解得∴()2 012=1.
19.分析:根据轴对称图形的性质,分别在图甲、图乙中再将两个空白的小正方形涂黑,使它成为轴对称图形即可.
解:如图所示.(答案不唯一)
20.解:∵ △ABC是等边三角形,
∴ AB=BC=CA,∠ABC=∠BCA=∠CAB=60°.
又∵ ∠1=∠2=∠3,
∴ ∠BAC-∠1=∠ABC-∠2=∠BCA-∠3,
即∠CAF=∠ABD=∠BCE.
在△ABD和△BCE和△CAF中,
∴ △ABD≌△BCE≌△CAF(ASA).
∴ AD=BE=CF,BD=CE=AF.∴ AD-AF=BE-BD=CF-CE,
即FD=DE=EF.
∴ △DEF是等边三角形.
∴ ∠FED=60°.
∴ ∠BEC=180°-∠FED=180°-60°=120°.
21.分析:(1)易得y轴在C的右边一个单位,轴在C的下方3个单位;
(2)作出A,B,C三点关于y轴对称的三点,顺次连接即可;
(3)根据所在象限及与坐标轴的距离可得相应坐标.
解:(1)(2)如图所示;
(3)点B′的坐标为(2,1).
22.解:如图,分别作AB、BC的垂直平分线,相交于点P,
沿PA、PB、PC进行分割,得到的△PAB、△PBC、△PAC都是等腰三角形,都是轴对称图形.
23. (1)证明:∵ ABCD是长方形,∴ AD=BC,∠D=∠B=90°.
根据折叠的性质,有GC=AD,∠G=∠D,∴ GC=BC,∠G=∠B.
又∠GCF+∠ECF=90°,∠BCE+∠ECF=90°,∴ ∠GCF=∠BCE.∴ △FGC≌△EBC(ASA).
(2)解:由(1)知,四边形ECGF的面积=四边形EADF的面积=四边形EBCF的面积=矩形ABCD的面积的一半.
∵ AB=8,AD=4,∴ 矩形ABCD的面积=8×4=32,∴ 阴影部分的面积=16.
24.分析:欲证M是BE的中点,已知DM⊥BC,因此只需证DB=DE,即证∠DBE=∠E,根据BD是等边△ABC的中线可知∠DBC=30°,因此只需证∠E=30°.
证明:连接BD,
∵ △ABC是等边三角形,∴ ∠ABC=∠ACB=60°.
∵ CD=CE,∴ ∠CDE=∠E=30°.
∵ BD是AC边上的中线,∴ BD平分∠ABC,即∠DBC=30°,
∴ ∠DBE=∠E.∴ DB=DE.又∵ DM⊥BE,
∴ DM是BE边上的中线,即M是BE的中点.
25.解:如图所示,分别以直线、为对称轴,作点的对应点和,连接,交于点,交于点,则最短,即.
第3题图
第2题图
第5题图
第7题图
第10题图
第9题图
第12题图
第13题图
第15题图
第14题图
第16题图
第20题图
第21题图
第22题图
第25题图
第5题答图
第6题答图
第15题答图
第19题答图
第22题答图
第21题答图
O
P
M
N
第25题答图
Y
X
PAGE
1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
