第5章 生活中的轴对称 单元测试卷(二)
文档属性
| 名称 | 第5章 生活中的轴对称 单元测试卷(二) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 14:15:10 | ||
图片预览




文档简介
第5章《生活中的轴对称》单元测试
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1. 观察图形…并判断照此规律从左到右第四个图形是( )
A. B. C. D.
2. 如图的方格纸中,左边图形到右边图形的变换是( )
A.向右平移7格
B.以AB的垂直平分线为对称轴作轴对称变换,再以AB为对称轴作轴对称变换
C.绕AB的中点旋转180°,再以AB为对称轴作轴对称变换
D.以AB为对称轴作轴对称变换,再向右平移7格
3. 如图所示,△与△关于直线对称,则∠等于( )
A. B. C. D.
4. 下列说法正确的是( )
A.如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形
B.任何一个图形都有对称轴,有的图形不止一条对称轴
C.平面上两个大小、形状完全一样的图形一定关于某直线对称
D.如果△ABC和△EFG成轴对称,那么它们的面积一定相等
5. 如图所示,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点的三角形共有( )
A.3个 B.4个 C.5个 D.6个
6. 以下各命题中,正确的命题是( )
(1)等腰三角形的一边长为4 cm,一边长为9 cm,则它的周长为17 cm或22 cm;
(2)三角形的一个外角等于两个内角的和;
(3)有两边和一角对应相等的两个三角形全等;
(4)等边三角形是轴对称图形;
(5)三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A.(1)(2)(3) B.(1)(3)(5) C.(2)(4)(5) D.(4)(5)
7. 将一张正方形纸片如图所示折叠两次,并在上面剪下一个菱形小洞,纸片展开后是( )
A. B. C. D.
8. 下列说法正确的是( ) 来源:http://www./tiku/
A.轴对称图形是两个图形组成的
B.等边三角形有三条对称轴
C.两个全等的三角形组成一个轴对称图形
D.直角三角形一定是轴对称图形
9. 如图所示,在3×3正方形网格中,已有三个小正方形被涂黑,将剩余的白色小正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有( )
A.6种 B.5种 C.4种 D.2种
10. 如图所示,在△中,,∠,的垂直平分线交于,交于,下列结论错误的是( )
A.平分∠ B.△的周长等于
C. D.点是线段的中点
二、填空题(每小题3分,共24分)
11. 一位交警在执勤过程中,从汽车的后视镜中看见某车牌照的后5位号码是,该车牌的后5位号码实际是 .
12. 光线以如图所示的角度照射到平面镜上,然后在平面镜Ⅰ、Ⅱ间来回反射,已知=60°,β=50°,则= .
13. 如图,在△ABC中,AB=5 cm,AC=3 cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为 cm.
14. 如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E= 度. 来源:http://www./tiku/
15. 如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是 .
16. 如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AD交BC于点D,DE∥AC,DE交AB于点E ,M为BE的中点,连结DM. 在不添加任何辅助线和字母的情况下,图中的等腰三角形是 .(写出一个即可)
17. 如图所示,P是等边三角形ABC内一点,将△ABP绕点B顺时针方向旋转60°,得到△CBP′.若PB=3,则PP′= .
18. 如图所示,是∠的平分线,于点,于,则关于直线对称的三角形共有_______对.
三、解答题(共46分)
19.(6分)如图所示,在等边△中,分别平分∠和△的外角∠,∥交于点,求证:.
20. (6分)如图所示,∥∠的平分线与∠的平分线交于点,过点的直线垂直于,垂足为,交于点.试问:点是线段的中点吗?为什么?
21. (6分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于轴对称的△A′B′C′;
(3)写出点B′的坐标. 来源:http://www./tiku/
22. (6分)公园内有一块三角形空地(如图所示),现要将它分割成三块,种植三种不同的花卉,为了美观,要求每块都要是轴对称图形,请你在图中画出分割线,保留必要的画图痕迹.
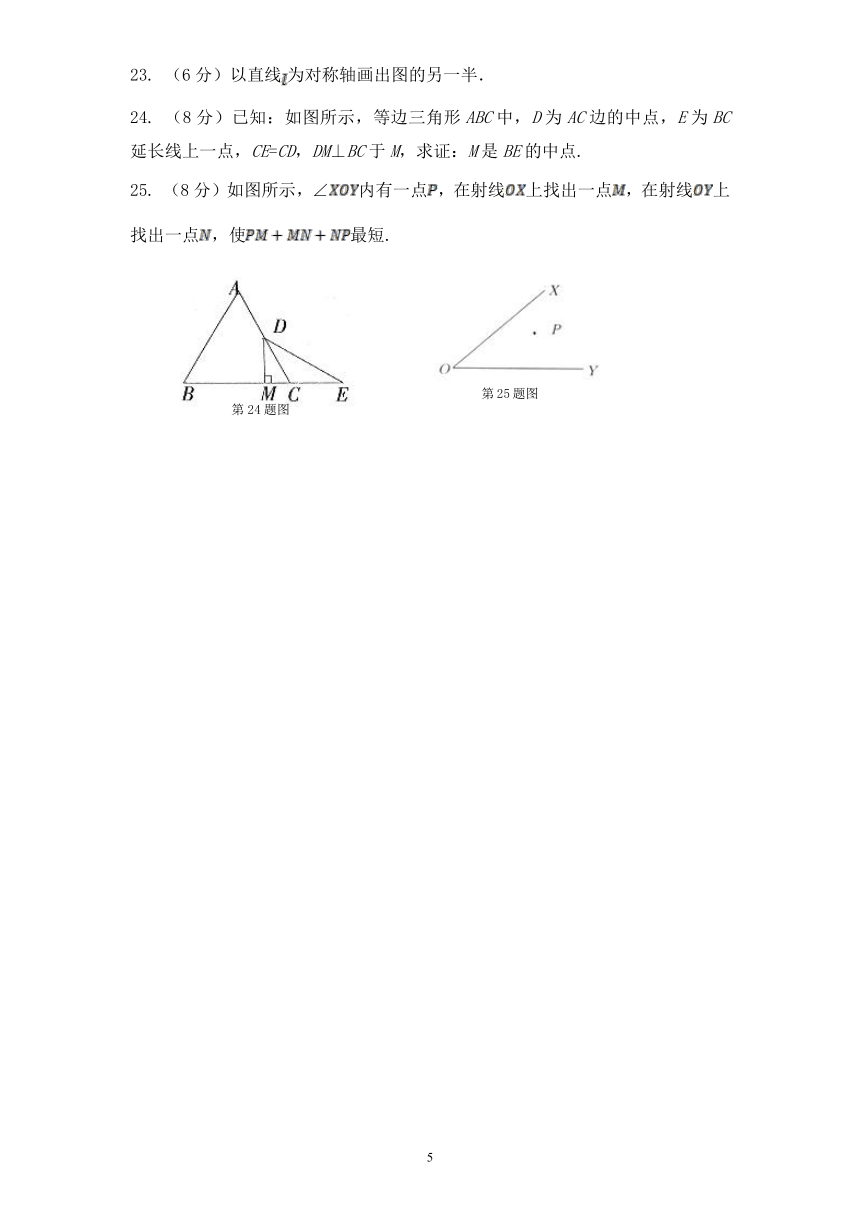
23. (6分)以直线为对称轴画出图的另一半.
24. (8分)已知:如图所示,等边三角形ABC中,D为AC边的中点,E为BC延长线上一点,CE=CD,DM⊥BC于M,求证:M是BE的中点.
25. (8分)如图所示,∠内有一点,在射线上找出一点,在射线上找出一点,使最短.
参考答案
1. D 解析:观察图形可知:单独涂黑的角顺时针旋转,只有D符合.故选D.
2. D 解析:观察可得:要使左边图形变化到右边图形,首先以AB为对称轴作轴对称变换,再向右平移7格.故选D.
3. D 解析:因为 △与△关于直线对称,
所以所以.
4. D 解析:A.如果图形甲和图形乙关于直线MN对称,则图形甲不一定是轴对称图形,
错误;
B.有的图形没有对称轴,错误;
C.平面上两个大小、形状完全一样的图形不一定关于某直线对称,与摆放位置有关,错误;
D.如果△ABC和△EFG成轴对称,那么它们全等,故其面积一定相等,正确.故选D.
5. C 解析:与△ABC成轴对称且以格点为顶点的三角形有
△ABG、△CDF、△AEF、△DBH,△BCG共5个,故选C.
6. D 解析:(1)等腰三角形的一边长为4 cm,一边长为9 cm,则三边长为9 cm,9 cm,4 cm,或4 cm,4 cm,9 cm,因为4+4<9,则它的周长只能是22 cm,故此命题错误;
(2)三角形的一个外角等于与它不相邻的两个内角的和,故此命题错误;
(3)有两边和一角对应相等的两个三角形全等错误,必须是夹角;
(4)等边三角形是轴对称图形,此命题正确;
(5)三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形,正确.
如图所示:∵ AD∥BC,∴ ∠1=∠B,∠2=∠C.
∵ AD是角平分线,∴ ∠1=∠2,
∴ ∠B =∠C,∴ AB =AC.
即△ABC是等腰三角形.故选D.
7. C 解析:当正方形纸片两次沿对角线对折成为一直角三角形时,在垂直于斜边的位置上剪菱形,则直角顶点处完好,即原正方形中间无损,且菱形关于对角线对称.故选C.
8. B 解析:A.轴对称图形是指1个图形,故错误;
B.等边三角形有三条对称轴,即三条中线所在直线,故正确;
C.两个全等的三角形不一定组成一个轴对称图形,故错误;
D.直角三角形不一定是轴对称图形,只有等腰直角三角形是轴对称图形,故错误.
故选B.
9. C 解析:根据题意,涂黑每一个格都会出现一种等可能情况,共出现6种等可能情况,
而当涂黑左上角和右下角的小正方形时,不会是轴对称图形,其余的4种情况均可以.
故选C.
10. D 解析:因为在△中,,∠,所以∠∠.
因为的垂直平分线是,所以,所以∠∠,
所以∠∠∠∠,
所以平分∠,故正确.
所以△的周长为,故正确.
因为∠,∠,所以∠∠∠,
所以∠∠,所以,所以,故正确.
因为,所以,所以点不是线段的中点,故错误.故选.
11. BA629 解析:关于镜面对称,也可以看成是关于某条直线对称,关于某条直线对称的数字依次是BA629.
12. 40° 解析:=180°-[60°+(180°-100°)]=40°.
13. 8 14. 15
15. 3 解析:要使△PBG的周长最小,而BG=1一定,只要使BP+PG最短即可.
连接AG交EF于M.
∵ △ABC是等边三角形,E、F、G分别为AB、AC、BC的中点,
∴ AG⊥BC,EF∥BC,
∴ AG⊥EF,AM=MG,
∴ A、G关于EF对称,
∴ P点与点E重合时,BP+PG最小,
即△PBG的周长最小,
最小值是:PB +PG +BG =AE +BE +BG =AB +BG =2+1=3.
16. △MBD或△MDE或△EAD 解析:由∠ACB=90°,DE∥AC,得∠EDC=90°,又M为BE的中点,得MB=MD=ME,∴△MBD和△MDE是等腰三角形,
∵∠BAC的平分线AD交BC于点D,DE∥AC,∴∠EDA=∠EAD=∠DAC,
∴△EAD是等腰三角形.
17. 3 解析:∵ △ABP绕点B顺时针方向旋转60°得到△CBP′,
∴ ∠PBP′=60°,BP=BP′,
∴ △BPP′为等边三角形,
∴ PP′=BP=3.
18. 解析:△和△,△和△△和△△和△共4对.
19. 证明:因为分别平分∠和∠,
所以∠∠,∠∠.
因为∥,所以∠∠,∠∠.
所以∠∠,∠∠.
所以.所以.
20. 解:点是线段的中点.理由如下:
过点作于点
因为∥所以.
又因为∠的平分线,是∠的平分线,
所以所以
所以点是线段的中点.
21. 分析:(1)易得y轴在C的右边一个单位,轴在C的下方3个单位;
(2)作出A,B,C三点关于y轴对称的三点,顺次连接即可;
(3)根据所在象限及与坐标轴的距离可得相应坐标.
解:(1)(2)如图所示;
(3)点B′的坐标为(2,1).
22. 解:如图,分别作AB、BC的垂直平分线,相交于点P,
沿PA、PB、PC进行分割,
得到的△PAB、△PBC、△PAC都是等腰三角形,都是轴对称图形.
23. 分析:作图形的对称图形首先作出各顶点的对称点,然后连接各对称点即为原图形的对称图形.
解:作对称图形得:作圆弧的对称图形时以原来圆弧的圆心为圆心,原半径为半径作出圆弧的对称图形.对于矩形的对称图形和外框图形的对称图形首先作出各顶点关于的对称点,连接对称点即为原图形的对称图形.
24. 分析:欲证M是BE的中点,已知DM⊥BC,因此只需证DB=DE,即证∠DBE=∠E,根据BD是等边△ABC的中线可知∠DBC=30°,因此只需证∠E=30°.
证明:连结BD,
∵ △ABC是等边三角形,∴ ∠ABC=∠ACB=60°.
∵ CD=CE,∴ ∠CDE=∠E=30°.
∵ BD是AC边上的中线,∴ BD平分∠ABC,即∠DBC=30°,
∴ ∠DBE=∠E.∴ DB=DE.又∵ DM⊥BE,
∴ DM是BE边上的中线,即M是BE的中点.
25. 解:如图所示,分别以直线、为对称轴,作点的对应点和,连接,交于,交于,则最短.
第3题图
第2题图
第5题图
第7题图
第9题图
第10题图
第12题图
第14题图
第15题图
第13题图
第16题图
A
B
D
C
O
E
第18题图
第17题图
A
B
C
D
P
第20题图
第21题图
第23题图
第22题图
第25题图
第24题图
第5题答图
第6题答图
第15题答图
第21题答图
第22题答图
第23题答图
O
P
M
N
第25题答图
Y
X
第24题答图
PAGE
1
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1. 观察图形…并判断照此规律从左到右第四个图形是( )
A. B. C. D.
2. 如图的方格纸中,左边图形到右边图形的变换是( )
A.向右平移7格
B.以AB的垂直平分线为对称轴作轴对称变换,再以AB为对称轴作轴对称变换
C.绕AB的中点旋转180°,再以AB为对称轴作轴对称变换
D.以AB为对称轴作轴对称变换,再向右平移7格
3. 如图所示,△与△关于直线对称,则∠等于( )
A. B. C. D.
4. 下列说法正确的是( )
A.如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形
B.任何一个图形都有对称轴,有的图形不止一条对称轴
C.平面上两个大小、形状完全一样的图形一定关于某直线对称
D.如果△ABC和△EFG成轴对称,那么它们的面积一定相等
5. 如图所示,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点的三角形共有( )
A.3个 B.4个 C.5个 D.6个
6. 以下各命题中,正确的命题是( )
(1)等腰三角形的一边长为4 cm,一边长为9 cm,则它的周长为17 cm或22 cm;
(2)三角形的一个外角等于两个内角的和;
(3)有两边和一角对应相等的两个三角形全等;
(4)等边三角形是轴对称图形;
(5)三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A.(1)(2)(3) B.(1)(3)(5) C.(2)(4)(5) D.(4)(5)
7. 将一张正方形纸片如图所示折叠两次,并在上面剪下一个菱形小洞,纸片展开后是( )
A. B. C. D.
8. 下列说法正确的是( ) 来源:http://www./tiku/
A.轴对称图形是两个图形组成的
B.等边三角形有三条对称轴
C.两个全等的三角形组成一个轴对称图形
D.直角三角形一定是轴对称图形
9. 如图所示,在3×3正方形网格中,已有三个小正方形被涂黑,将剩余的白色小正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有( )
A.6种 B.5种 C.4种 D.2种
10. 如图所示,在△中,,∠,的垂直平分线交于,交于,下列结论错误的是( )
A.平分∠ B.△的周长等于
C. D.点是线段的中点
二、填空题(每小题3分,共24分)
11. 一位交警在执勤过程中,从汽车的后视镜中看见某车牌照的后5位号码是,该车牌的后5位号码实际是 .
12. 光线以如图所示的角度照射到平面镜上,然后在平面镜Ⅰ、Ⅱ间来回反射,已知=60°,β=50°,则= .
13. 如图,在△ABC中,AB=5 cm,AC=3 cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为 cm.
14. 如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E= 度. 来源:http://www./tiku/
15. 如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是 .
16. 如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AD交BC于点D,DE∥AC,DE交AB于点E ,M为BE的中点,连结DM. 在不添加任何辅助线和字母的情况下,图中的等腰三角形是 .(写出一个即可)
17. 如图所示,P是等边三角形ABC内一点,将△ABP绕点B顺时针方向旋转60°,得到△CBP′.若PB=3,则PP′= .
18. 如图所示,是∠的平分线,于点,于,则关于直线对称的三角形共有_______对.
三、解答题(共46分)
19.(6分)如图所示,在等边△中,分别平分∠和△的外角∠,∥交于点,求证:.
20. (6分)如图所示,∥∠的平分线与∠的平分线交于点,过点的直线垂直于,垂足为,交于点.试问:点是线段的中点吗?为什么?
21. (6分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于轴对称的△A′B′C′;
(3)写出点B′的坐标. 来源:http://www./tiku/
22. (6分)公园内有一块三角形空地(如图所示),现要将它分割成三块,种植三种不同的花卉,为了美观,要求每块都要是轴对称图形,请你在图中画出分割线,保留必要的画图痕迹.
23. (6分)以直线为对称轴画出图的另一半.
24. (8分)已知:如图所示,等边三角形ABC中,D为AC边的中点,E为BC延长线上一点,CE=CD,DM⊥BC于M,求证:M是BE的中点.
25. (8分)如图所示,∠内有一点,在射线上找出一点,在射线上找出一点,使最短.
参考答案
1. D 解析:观察图形可知:单独涂黑的角顺时针旋转,只有D符合.故选D.
2. D 解析:观察可得:要使左边图形变化到右边图形,首先以AB为对称轴作轴对称变换,再向右平移7格.故选D.
3. D 解析:因为 △与△关于直线对称,
所以所以.
4. D 解析:A.如果图形甲和图形乙关于直线MN对称,则图形甲不一定是轴对称图形,
错误;
B.有的图形没有对称轴,错误;
C.平面上两个大小、形状完全一样的图形不一定关于某直线对称,与摆放位置有关,错误;
D.如果△ABC和△EFG成轴对称,那么它们全等,故其面积一定相等,正确.故选D.
5. C 解析:与△ABC成轴对称且以格点为顶点的三角形有
△ABG、△CDF、△AEF、△DBH,△BCG共5个,故选C.
6. D 解析:(1)等腰三角形的一边长为4 cm,一边长为9 cm,则三边长为9 cm,9 cm,4 cm,或4 cm,4 cm,9 cm,因为4+4<9,则它的周长只能是22 cm,故此命题错误;
(2)三角形的一个外角等于与它不相邻的两个内角的和,故此命题错误;
(3)有两边和一角对应相等的两个三角形全等错误,必须是夹角;
(4)等边三角形是轴对称图形,此命题正确;
(5)三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形,正确.
如图所示:∵ AD∥BC,∴ ∠1=∠B,∠2=∠C.
∵ AD是角平分线,∴ ∠1=∠2,
∴ ∠B =∠C,∴ AB =AC.
即△ABC是等腰三角形.故选D.
7. C 解析:当正方形纸片两次沿对角线对折成为一直角三角形时,在垂直于斜边的位置上剪菱形,则直角顶点处完好,即原正方形中间无损,且菱形关于对角线对称.故选C.
8. B 解析:A.轴对称图形是指1个图形,故错误;
B.等边三角形有三条对称轴,即三条中线所在直线,故正确;
C.两个全等的三角形不一定组成一个轴对称图形,故错误;
D.直角三角形不一定是轴对称图形,只有等腰直角三角形是轴对称图形,故错误.
故选B.
9. C 解析:根据题意,涂黑每一个格都会出现一种等可能情况,共出现6种等可能情况,
而当涂黑左上角和右下角的小正方形时,不会是轴对称图形,其余的4种情况均可以.
故选C.
10. D 解析:因为在△中,,∠,所以∠∠.
因为的垂直平分线是,所以,所以∠∠,
所以∠∠∠∠,
所以平分∠,故正确.
所以△的周长为,故正确.
因为∠,∠,所以∠∠∠,
所以∠∠,所以,所以,故正确.
因为,所以,所以点不是线段的中点,故错误.故选.
11. BA629 解析:关于镜面对称,也可以看成是关于某条直线对称,关于某条直线对称的数字依次是BA629.
12. 40° 解析:=180°-[60°+(180°-100°)]=40°.
13. 8 14. 15
15. 3 解析:要使△PBG的周长最小,而BG=1一定,只要使BP+PG最短即可.
连接AG交EF于M.
∵ △ABC是等边三角形,E、F、G分别为AB、AC、BC的中点,
∴ AG⊥BC,EF∥BC,
∴ AG⊥EF,AM=MG,
∴ A、G关于EF对称,
∴ P点与点E重合时,BP+PG最小,
即△PBG的周长最小,
最小值是:PB +PG +BG =AE +BE +BG =AB +BG =2+1=3.
16. △MBD或△MDE或△EAD 解析:由∠ACB=90°,DE∥AC,得∠EDC=90°,又M为BE的中点,得MB=MD=ME,∴△MBD和△MDE是等腰三角形,
∵∠BAC的平分线AD交BC于点D,DE∥AC,∴∠EDA=∠EAD=∠DAC,
∴△EAD是等腰三角形.
17. 3 解析:∵ △ABP绕点B顺时针方向旋转60°得到△CBP′,
∴ ∠PBP′=60°,BP=BP′,
∴ △BPP′为等边三角形,
∴ PP′=BP=3.
18. 解析:△和△,△和△△和△△和△共4对.
19. 证明:因为分别平分∠和∠,
所以∠∠,∠∠.
因为∥,所以∠∠,∠∠.
所以∠∠,∠∠.
所以.所以.
20. 解:点是线段的中点.理由如下:
过点作于点
因为∥所以.
又因为∠的平分线,是∠的平分线,
所以所以
所以点是线段的中点.
21. 分析:(1)易得y轴在C的右边一个单位,轴在C的下方3个单位;
(2)作出A,B,C三点关于y轴对称的三点,顺次连接即可;
(3)根据所在象限及与坐标轴的距离可得相应坐标.
解:(1)(2)如图所示;
(3)点B′的坐标为(2,1).
22. 解:如图,分别作AB、BC的垂直平分线,相交于点P,
沿PA、PB、PC进行分割,
得到的△PAB、△PBC、△PAC都是等腰三角形,都是轴对称图形.
23. 分析:作图形的对称图形首先作出各顶点的对称点,然后连接各对称点即为原图形的对称图形.
解:作对称图形得:作圆弧的对称图形时以原来圆弧的圆心为圆心,原半径为半径作出圆弧的对称图形.对于矩形的对称图形和外框图形的对称图形首先作出各顶点关于的对称点,连接对称点即为原图形的对称图形.
24. 分析:欲证M是BE的中点,已知DM⊥BC,因此只需证DB=DE,即证∠DBE=∠E,根据BD是等边△ABC的中线可知∠DBC=30°,因此只需证∠E=30°.
证明:连结BD,
∵ △ABC是等边三角形,∴ ∠ABC=∠ACB=60°.
∵ CD=CE,∴ ∠CDE=∠E=30°.
∵ BD是AC边上的中线,∴ BD平分∠ABC,即∠DBC=30°,
∴ ∠DBE=∠E.∴ DB=DE.又∵ DM⊥BE,
∴ DM是BE边上的中线,即M是BE的中点.
25. 解:如图所示,分别以直线、为对称轴,作点的对应点和,连接,交于,交于,则最短.
第3题图
第2题图
第5题图
第7题图
第9题图
第10题图
第12题图
第14题图
第15题图
第13题图
第16题图
A
B
D
C
O
E
第18题图
第17题图
A
B
C
D
P
第20题图
第21题图
第23题图
第22题图
第25题图
第24题图
第5题答图
第6题答图
第15题答图
第21题答图
第22题答图
第23题答图
O
P
M
N
第25题答图
Y
X
第24题答图
PAGE
1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
