数学五年级下册沪教版 4.9表面积的变化课件(共18张PPT)
文档属性
| 名称 | 数学五年级下册沪教版 4.9表面积的变化课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 15:24:39 | ||
图片预览



文档简介
(共18张PPT)
1cm
1cm
1cm
一个面的面积是( )
它的表面积是( )
它的体积是( )
1cm2
6cm2
1cm3
……
101个小正方体
拼成的长方体的表面积比原来单个正方体的表面积之和减少了多少呢?
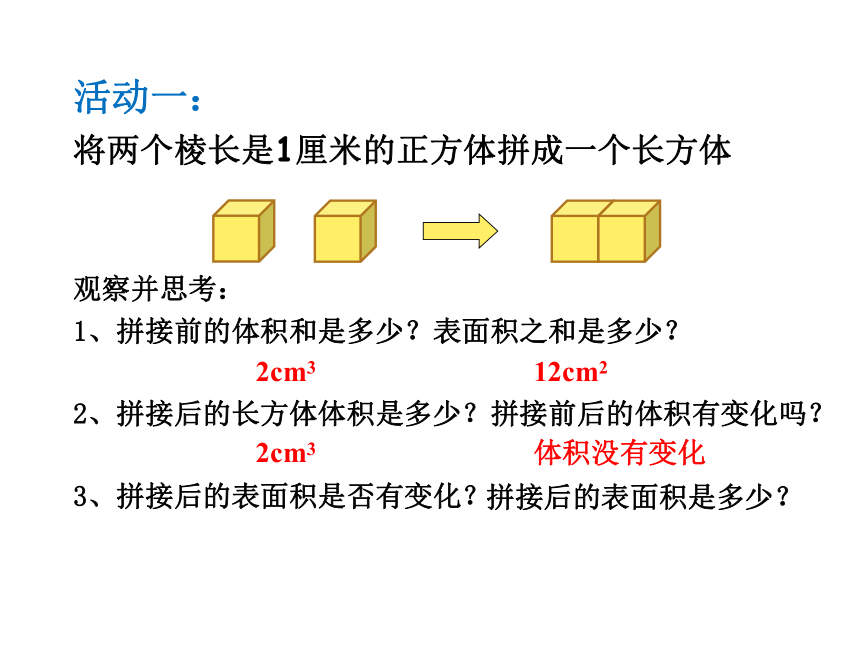
活动一:
将两个棱长是1厘米的正方体拼成一个长方体
观察并思考:
1、拼接前的体积和是多少?表面积之和是多少?
2、拼接后的长方体体积是多少?拼接前后的体积有变化吗?
3、拼接后的表面积是否有变化?
12cm2
2cm3
2cm3
体积没有变化
拼接后的表面积是多少?
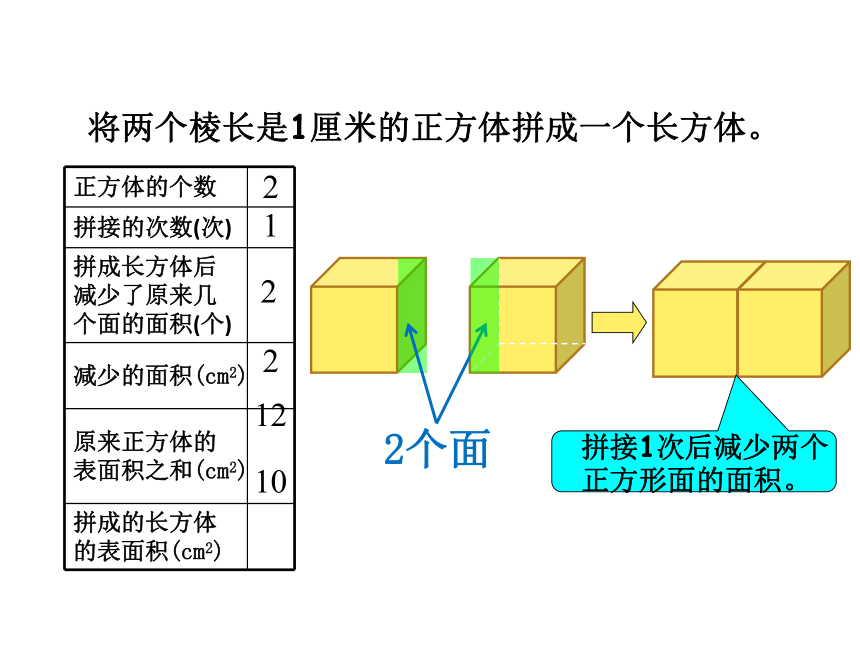
将两个棱长是1厘米的正方体拼成一个长方体。
2个面
正方体的个数 2
拼接的次数(次)
拼成长方体后减少了原来几个面的面积(个)
减少的面积(cm2)
原来正方体的表面积之和(cm2)
拼成的长方体的表面积(cm2)
1
2
2
12
10
拼接1次后减少两个正方形面的面积。
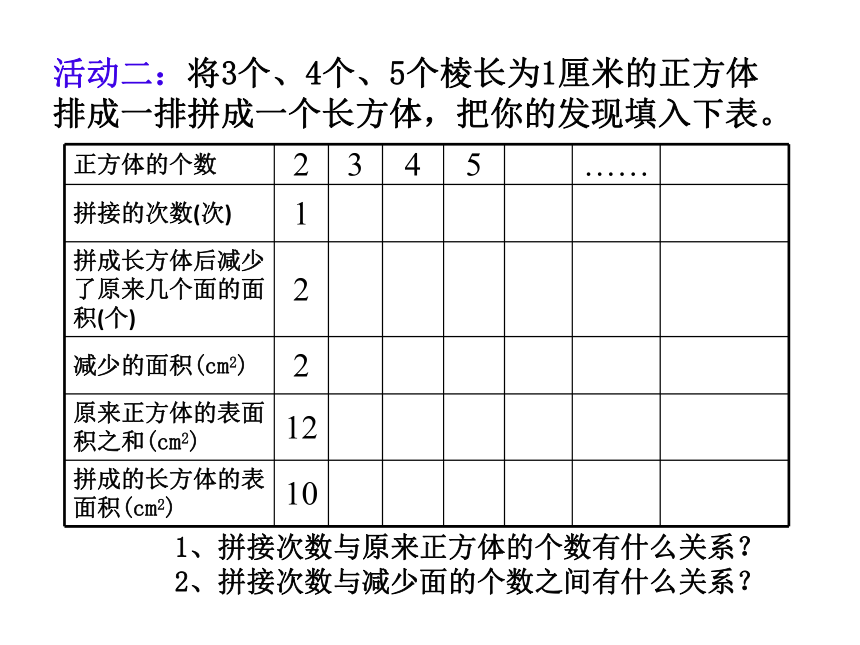
活动二:将3个、4个、5个棱长为1厘米的正方体排成一排拼成一个长方体,把你的发现填入下表。
正方体的个数 2 3 4 5 ……
拼接的次数(次) 1
拼成长方体后减少了原来几个面的面积(个) 2
减少的面积(cm2) 2
原来正方体的表面积之和(cm2) 12
拼成的长方体的表面积(cm2) 10
1、拼接次数与原来正方体的个数有什么关系?
2、拼接次数与减少面的个数之间有什么关系?
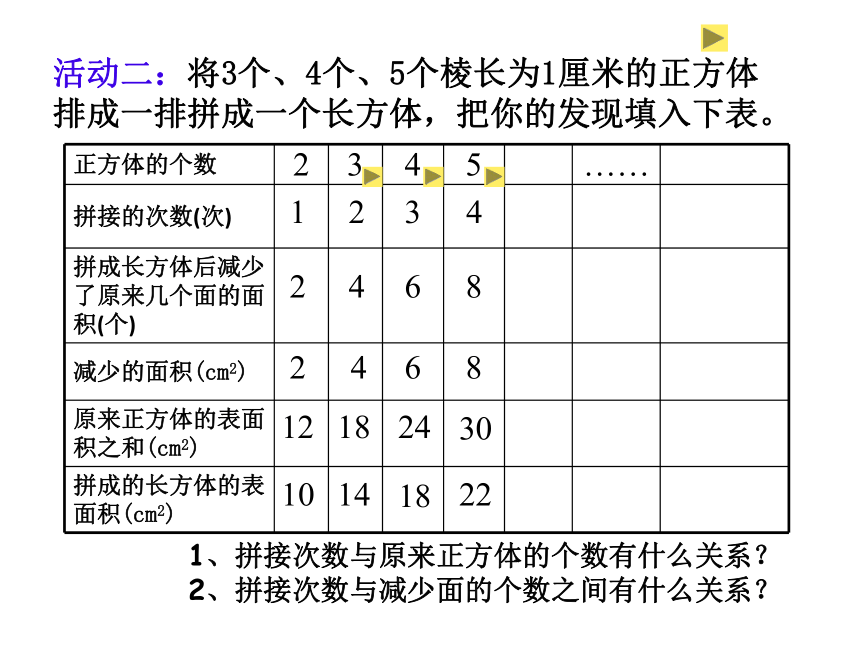
活动二:将3个、4个、5个棱长为1厘米的正方体排成一排拼成一个长方体,把你的发现填入下表。
正方体的个数 2 3 4 5 ……
拼接的次数(次)
拼成长方体后减少了原来几个面的面积(个)
减少的面积(cm2)
原来正方体的表面积之和(cm2)
拼成的长方体的表面积(cm2)
1
2
2
12
10
2
4
4
18
14
3
6
6
24
18
4
8
8
30
22
1、拼接次数与原来正方体的个数有什么关系? 2、拼接次数与减少面的个数之间有什么关系?
2个面
2个面
2个面
2个面
2个面
2个面
2个面
2个面
2个面
活动二:将2、3、4、5个棱长为1厘米的正方体排成一排拼成一个长方体,把你的发现填入下表。
正方体的个数 2 3 4 5 ……
拼接的次数(次)
拼成长方体后减少了原来几个面的面积(个)
减少的面积(cm2)
原来正方体的表面积之和(cm2)
拼成的长方体的表面积(cm2)
1
2
2
12
10
2
4
4
18
14
3
6
6
24
18
4
8
8
30
22
5
10
10
36
26
6
n
n-1
2(n-1)
2(n-1)
6n
6n-2(n-1)
1、拼接次数与原来正方体的个数有什么关系? 2、拼接次数与减少面的个数之间有什么关系?
1、将4个棱长为1厘米的小正方体,如下图的方式拼成一个长方体,拼成的长方体表面积比原来4个小正方体的表面积之和减少了( )个小正方形面的面积,减少了( )平方厘米。
2、将4个棱长为2厘米的小正方体,如下图的方式拼成一个长方体,拼成的长方体表面积比原来4个小正方体的表面积之和减少了( )个小正方形面的面积,减少了( )平方厘米。
看图填空:
6
6
6
24
选择:
(1)7个相同的小正方体拼成一个新的长方体,这个新长方体的表面积比原来减少了( )个小正方形面的面积。
① 6 ② 7 ③ 12 ④ 14
③
(2)把一个长方体木条锯成大小相等的4个正方体,共增加了( )个面的面积。
① 8 ② 6 ③ 4 ④ 3
2个面
2个面
2个面
②
(3)把棱长为2厘米的3个正方体拼成一个长方体(如下图),拼成的长方体表面积比原来3个正方体的表面积之和减少了( )平方厘米。
① 4 ② 8 ③ 12 ④ 16
④
(4)一个棱长为4厘米的正方体,在它的角上挖掉一块棱长为2厘米的小正方体(如图)它的表面积( )。
① 增加 ② 减少 ③ 不变 ④ 无法确定
选择:
③
(如图)把一个长为8分米的长方体木条锯成4个大小相等的小正方体,这4个小正方体的表面积总和比原来这个长方体的表面积增加了多少平方分米?
8分米
计算:
活动三:操作探究
用4个体积是1立方厘米的小正方体拼成一个长方体,有几种拼法?拼成的长方体的表面积比原来4个小正方体表面积之和减少了多少平方厘米?
减少了6个面的面积(6cm2)
减少了8个面的面积(8cm2)
2个面
2个面
2个面
2个面
活动四:拓展提高
如果你是纸箱厂的设计员,要设计一种正好能装8个棱长为1厘米的小正方体的纸盒,你将如何设计?你有几种设计方案?哪种方案材料最节省?
1cm
1cm
1cm
一个面的面积是( )
它的表面积是( )
它的体积是( )
1cm2
6cm2
1cm3
……
101个小正方体
拼成的长方体的表面积比原来单个正方体的表面积之和减少了多少呢?
活动一:
将两个棱长是1厘米的正方体拼成一个长方体
观察并思考:
1、拼接前的体积和是多少?表面积之和是多少?
2、拼接后的长方体体积是多少?拼接前后的体积有变化吗?
3、拼接后的表面积是否有变化?
12cm2
2cm3
2cm3
体积没有变化
拼接后的表面积是多少?
将两个棱长是1厘米的正方体拼成一个长方体。
2个面
正方体的个数 2
拼接的次数(次)
拼成长方体后减少了原来几个面的面积(个)
减少的面积(cm2)
原来正方体的表面积之和(cm2)
拼成的长方体的表面积(cm2)
1
2
2
12
10
拼接1次后减少两个正方形面的面积。
活动二:将3个、4个、5个棱长为1厘米的正方体排成一排拼成一个长方体,把你的发现填入下表。
正方体的个数 2 3 4 5 ……
拼接的次数(次) 1
拼成长方体后减少了原来几个面的面积(个) 2
减少的面积(cm2) 2
原来正方体的表面积之和(cm2) 12
拼成的长方体的表面积(cm2) 10
1、拼接次数与原来正方体的个数有什么关系?
2、拼接次数与减少面的个数之间有什么关系?
活动二:将3个、4个、5个棱长为1厘米的正方体排成一排拼成一个长方体,把你的发现填入下表。
正方体的个数 2 3 4 5 ……
拼接的次数(次)
拼成长方体后减少了原来几个面的面积(个)
减少的面积(cm2)
原来正方体的表面积之和(cm2)
拼成的长方体的表面积(cm2)
1
2
2
12
10
2
4
4
18
14
3
6
6
24
18
4
8
8
30
22
1、拼接次数与原来正方体的个数有什么关系? 2、拼接次数与减少面的个数之间有什么关系?
2个面
2个面
2个面
2个面
2个面
2个面
2个面
2个面
2个面
活动二:将2、3、4、5个棱长为1厘米的正方体排成一排拼成一个长方体,把你的发现填入下表。
正方体的个数 2 3 4 5 ……
拼接的次数(次)
拼成长方体后减少了原来几个面的面积(个)
减少的面积(cm2)
原来正方体的表面积之和(cm2)
拼成的长方体的表面积(cm2)
1
2
2
12
10
2
4
4
18
14
3
6
6
24
18
4
8
8
30
22
5
10
10
36
26
6
n
n-1
2(n-1)
2(n-1)
6n
6n-2(n-1)
1、拼接次数与原来正方体的个数有什么关系? 2、拼接次数与减少面的个数之间有什么关系?
1、将4个棱长为1厘米的小正方体,如下图的方式拼成一个长方体,拼成的长方体表面积比原来4个小正方体的表面积之和减少了( )个小正方形面的面积,减少了( )平方厘米。
2、将4个棱长为2厘米的小正方体,如下图的方式拼成一个长方体,拼成的长方体表面积比原来4个小正方体的表面积之和减少了( )个小正方形面的面积,减少了( )平方厘米。
看图填空:
6
6
6
24
选择:
(1)7个相同的小正方体拼成一个新的长方体,这个新长方体的表面积比原来减少了( )个小正方形面的面积。
① 6 ② 7 ③ 12 ④ 14
③
(2)把一个长方体木条锯成大小相等的4个正方体,共增加了( )个面的面积。
① 8 ② 6 ③ 4 ④ 3
2个面
2个面
2个面
②
(3)把棱长为2厘米的3个正方体拼成一个长方体(如下图),拼成的长方体表面积比原来3个正方体的表面积之和减少了( )平方厘米。
① 4 ② 8 ③ 12 ④ 16
④
(4)一个棱长为4厘米的正方体,在它的角上挖掉一块棱长为2厘米的小正方体(如图)它的表面积( )。
① 增加 ② 减少 ③ 不变 ④ 无法确定
选择:
③
(如图)把一个长为8分米的长方体木条锯成4个大小相等的小正方体,这4个小正方体的表面积总和比原来这个长方体的表面积增加了多少平方分米?
8分米
计算:
活动三:操作探究
用4个体积是1立方厘米的小正方体拼成一个长方体,有几种拼法?拼成的长方体的表面积比原来4个小正方体表面积之和减少了多少平方厘米?
减少了6个面的面积(6cm2)
减少了8个面的面积(8cm2)
2个面
2个面
2个面
2个面
活动四:拓展提高
如果你是纸箱厂的设计员,要设计一种正好能装8个棱长为1厘米的小正方体的纸盒,你将如何设计?你有几种设计方案?哪种方案材料最节省?
