第3章 圆 单元测试卷(五)(含答案)
文档属性
| 名称 | 第3章 圆 单元测试卷(五)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 95.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 14:30:03 | ||
图片预览

文档简介
第三章 圆 单元测试
(时间:90分钟 满分:100分)
一.选择题(每小题3分,共30分)
1.两圆的圆心都在x轴上,且两圆相交于A,B两点,点A的坐标是(3,2),那么点B的坐标为 ( )
(A)(–3,2) (B)(3,–2) (C)(–3,–2) (D)(3,0)
2.如果两圆的半径分别为2和3,圆心距为5,那么这两个圆的位置关系是( )
(A)外离 (B)外切 (C)相交 (D)内切
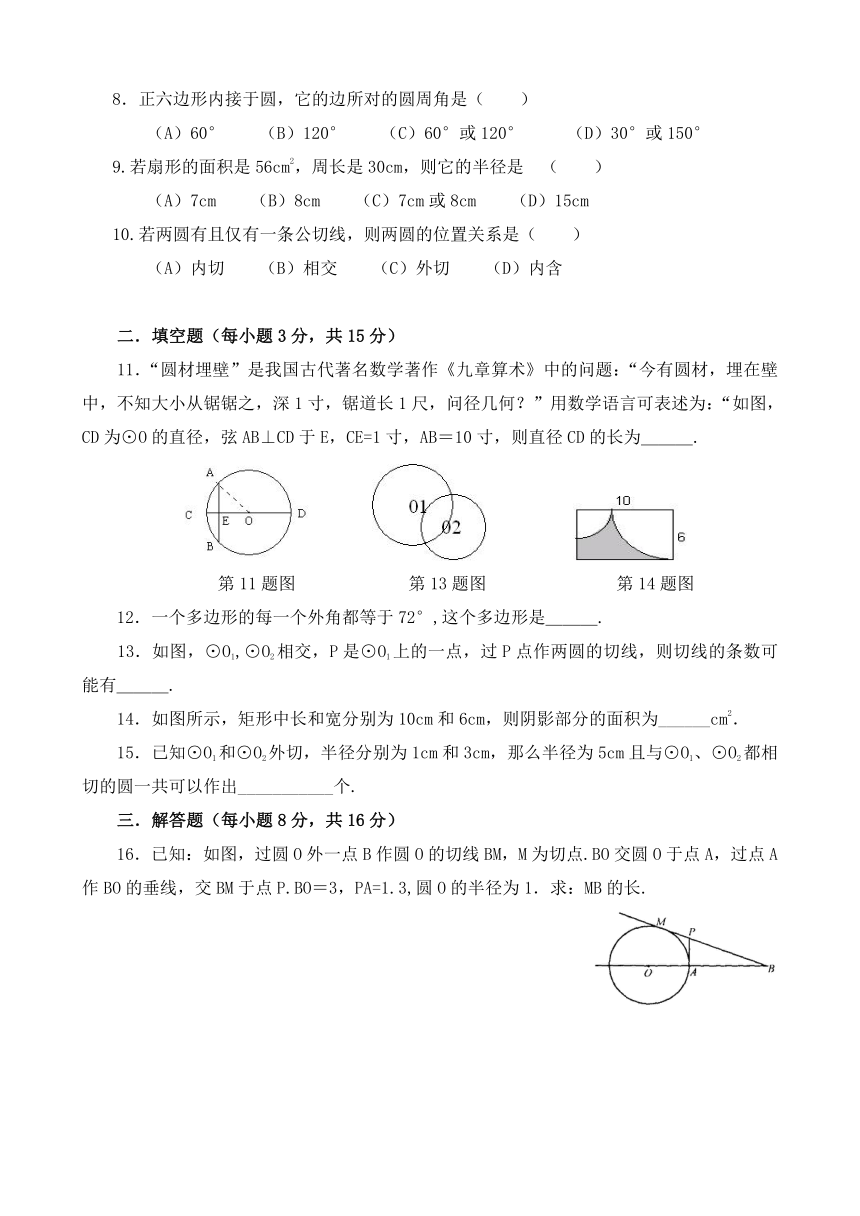
3.已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
(A)140° (B)120° (C)100° (D)80°
第3题图 第4题图 第5题图
4.如图,在⊙O中,直径CD与弦AB相交于点E,若BE=3,AE=4,DE=2,则⊙O的半径是 ( )
(A)3 (B)4 (C)6 (D)8
5.如图,过点P作⊙O的两条割线分别交⊙O于点A、B和点C、D,已知PA=3,AB=PC=2,若PA·PB=PC·PD,则PD的长是( )
(A)3 (B)7.5. (C)5 (D)5.5
6.使用直角钢尺检查某一工件是否恰好是半圆形的凹面,成半圆形的为合格,如图所示的四种情况中合格的是( )
两圆外切,半径分别为6、2,则这两圆的两条外公切线的夹角的度数是( )
(A)30° (B)60° C、90° D、120°
正六边形内接于圆,它的边所对的圆周角是( )
(A)60° (B)120° (C)60°或120° (D)30°或150°
9.若扇形的面积是56cm2,周长是30cm,则它的半径是 ( )
(A)7cm (B)8cm (C)7cm或8cm (D)15cm
10.若两圆有且仅有一条公切线,则两圆的位置关系是( )
(A)内切 (B)相交 (C)外切 (D)内含
二.填空题(每小题3分,共15分)
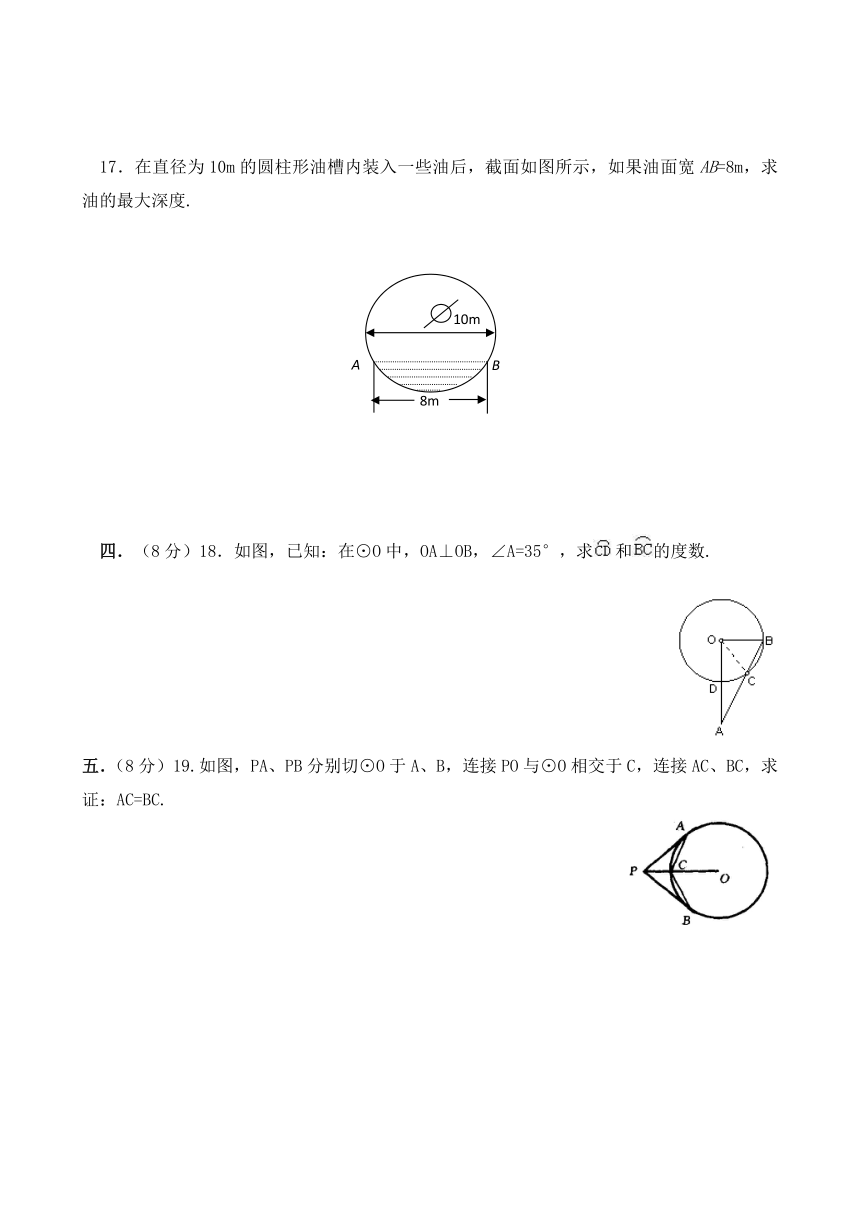
11.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小从锯锯之,深1寸,锯道长1尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为___.
第11题图 第13题图 第14题图
12.一个多边形的每一个外角都等于72°,这个多边形是___.
13.如图,⊙O1,⊙O2相交,P是⊙O1上的一点,过P点作两圆的切线,则切线的条数可能有___.
14.如图所示,矩形中长和宽分别为10cm和6cm,则阴影部分的面积为______cm2.
15.已知⊙O1和⊙O2外切,半径分别为1cm和3cm,那么半径为5cm且与⊙O1、⊙O2都相切的圆一共可以作出___________个.
三.解答题(每小题8分,共16分)
16.已知:如图,过圆O外一点B作圆O的切线BM,M为切点.BO交圆O于点A,过点A作BO的垂线,交BM于点P.BO=3,PA=1.3,圆O的半径为1.求:MB的长.
17.在直径为10m的圆柱形油槽内装入一些油后,截面如图所示,如果油面宽AB=8m,求油的最大深度.
四.(8分)18.如图,已知:在⊙O中,OA⊥OB,∠A=35°,求和的度数.
五.(8分)19.如图,PA、PB分别切⊙O于A、B,连接PO与⊙O相交于C,连接AC、BC,求证:AC=BC.
六.(10分)20.(1)如图(1),若⊙O1、⊙O2外切于A,BC是⊙O1、⊙O2的一条外公切线,B、C是切点,则AB⊥AC.
(2)如图(2),增加添加,连心线O1O2分别交⊙O1、⊙O2于M、N,BM、CN的延长线交于P,则BP与CP是否垂直?证明你的结论.
(3)如图(3),⊙O1与⊙O2相交,BC是两圆的外公切线,B、C是切点,连心线O1O2分别交两圆于M、N,Q是MN上一点,连结BQ、CQ则与BQ是否垂直?证明你的结论.
图(1) 图(2) 图(3)
七、探究题(13分)
21.如图,一个圆形街心花园,有三个出口A,B,C,每两个出口之间有一条60米长的道路,组成正三角形ABC,在中心点O处有一亭子,为使亭子与原有的道路相通,需再修三条小路OD,OE,OF,使另一出口D、E、F分别落在ΔABC分成三个全等的多边形,以备种植不同品种的花草.
(1)请你按以上要求设计两种不同的方案,将你的设计方案分别画在图1,图2中,并附简单说明.
(2)要使三条小路把ΔABC分成三个全等的等腰梯形,应怎样设计?请把方案画在图3中,并求此时三条小路的总长.
(3)请你探究出一种一般方法,使得出口D不论在什么位置,都能准确地找到另外两个出口E、F的位置,请写明这个方法.
(4)你在(3)中探究出的一般方法适用于正五边形吗?请结合图5予以说明,这种方法能推广到正n边形吗?
参考答案
一.1.B;由对称性知(3,-2).
2.B;提示:2+3=5,两圆半径等于圆心距.
3.C;提示:连OB、OC.
4.B;设圆的半径为R,由3×4=(R-2)(2R-2),R=4.
5.B;提示:由PA·PB=PC·PD.
6.C;直径所对的圆周角是直角.
7.B;转化为解直角三角形问.
8.D;圆内接正六边形的边长等于半径.
9.C;根据闪形面积公式.
10.A;两圆内切.
二.11.26寸; 12、正五边形; 13、一条或2条3条或4条; 14、60-13π; 15、4个.
三.提示:16、由切线长定理及其勾股定理得,BM=4.
17、2m.
四.18、分析:连结OC,通过求圆心角的度数求解.
解:连结OC,
在Rt△AOB中,∠A=35°,
∴∠B=55°,又∵OC=OB,
∴∠COB=180°-2∠B=70°,∴ 的度数为70°,
∠COD=90°-∠COB=90°-70°=20°,
∴ 的度数为20°.
五.19.提示:证明△PAC≌△PBC.
六、20.提示:(1)过点A作公切线;(2)易证BP与CP垂直;(3)中CQ与BQ不垂直.
七、[分析]:
21.(1)方案1:D,E,F与A,B,C重合,连OD,OE,OF.
方案2:OD,OE,OF分别垂直于AB,BC,AC.
(2)OD//AC,OE//AB,OF//BC, 如图(3),
作OM⊥BC于M,连OB,
∵ΔABC是等边三角形,∴BM=BC=30,且∠OBM=30°,
∴OM=10,
∵OE//AB,∴∠OEM=60°,OE==20,
又OE=OF=OD,∴OE+OF+OD=3OE=60,答:略.
(3)如图(4)方法1:在BC,CA,AB上分别截取BE=CF=AD,连结OD,OE,OF,
方法2:在AB上任取一点D,连OD,逆时针旋转OD120°两次,得E,F.
(4)设M1为A1A2上任一点,在各边上分别取A2M2=A3M3=A4M4=A5M5=A1M1,连OM1……OM5即可,
∴可推广到正n边形.
A
B
10m
8m
PAGE
(时间:90分钟 满分:100分)
一.选择题(每小题3分,共30分)
1.两圆的圆心都在x轴上,且两圆相交于A,B两点,点A的坐标是(3,2),那么点B的坐标为 ( )
(A)(–3,2) (B)(3,–2) (C)(–3,–2) (D)(3,0)
2.如果两圆的半径分别为2和3,圆心距为5,那么这两个圆的位置关系是( )
(A)外离 (B)外切 (C)相交 (D)内切
3.已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
(A)140° (B)120° (C)100° (D)80°
第3题图 第4题图 第5题图
4.如图,在⊙O中,直径CD与弦AB相交于点E,若BE=3,AE=4,DE=2,则⊙O的半径是 ( )
(A)3 (B)4 (C)6 (D)8
5.如图,过点P作⊙O的两条割线分别交⊙O于点A、B和点C、D,已知PA=3,AB=PC=2,若PA·PB=PC·PD,则PD的长是( )
(A)3 (B)7.5. (C)5 (D)5.5
6.使用直角钢尺检查某一工件是否恰好是半圆形的凹面,成半圆形的为合格,如图所示的四种情况中合格的是( )
两圆外切,半径分别为6、2,则这两圆的两条外公切线的夹角的度数是( )
(A)30° (B)60° C、90° D、120°
正六边形内接于圆,它的边所对的圆周角是( )
(A)60° (B)120° (C)60°或120° (D)30°或150°
9.若扇形的面积是56cm2,周长是30cm,则它的半径是 ( )
(A)7cm (B)8cm (C)7cm或8cm (D)15cm
10.若两圆有且仅有一条公切线,则两圆的位置关系是( )
(A)内切 (B)相交 (C)外切 (D)内含
二.填空题(每小题3分,共15分)
11.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小从锯锯之,深1寸,锯道长1尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为___.
第11题图 第13题图 第14题图
12.一个多边形的每一个外角都等于72°,这个多边形是___.
13.如图,⊙O1,⊙O2相交,P是⊙O1上的一点,过P点作两圆的切线,则切线的条数可能有___.
14.如图所示,矩形中长和宽分别为10cm和6cm,则阴影部分的面积为______cm2.
15.已知⊙O1和⊙O2外切,半径分别为1cm和3cm,那么半径为5cm且与⊙O1、⊙O2都相切的圆一共可以作出___________个.
三.解答题(每小题8分,共16分)
16.已知:如图,过圆O外一点B作圆O的切线BM,M为切点.BO交圆O于点A,过点A作BO的垂线,交BM于点P.BO=3,PA=1.3,圆O的半径为1.求:MB的长.
17.在直径为10m的圆柱形油槽内装入一些油后,截面如图所示,如果油面宽AB=8m,求油的最大深度.
四.(8分)18.如图,已知:在⊙O中,OA⊥OB,∠A=35°,求和的度数.
五.(8分)19.如图,PA、PB分别切⊙O于A、B,连接PO与⊙O相交于C,连接AC、BC,求证:AC=BC.
六.(10分)20.(1)如图(1),若⊙O1、⊙O2外切于A,BC是⊙O1、⊙O2的一条外公切线,B、C是切点,则AB⊥AC.
(2)如图(2),增加添加,连心线O1O2分别交⊙O1、⊙O2于M、N,BM、CN的延长线交于P,则BP与CP是否垂直?证明你的结论.
(3)如图(3),⊙O1与⊙O2相交,BC是两圆的外公切线,B、C是切点,连心线O1O2分别交两圆于M、N,Q是MN上一点,连结BQ、CQ则与BQ是否垂直?证明你的结论.
图(1) 图(2) 图(3)
七、探究题(13分)
21.如图,一个圆形街心花园,有三个出口A,B,C,每两个出口之间有一条60米长的道路,组成正三角形ABC,在中心点O处有一亭子,为使亭子与原有的道路相通,需再修三条小路OD,OE,OF,使另一出口D、E、F分别落在ΔABC分成三个全等的多边形,以备种植不同品种的花草.
(1)请你按以上要求设计两种不同的方案,将你的设计方案分别画在图1,图2中,并附简单说明.
(2)要使三条小路把ΔABC分成三个全等的等腰梯形,应怎样设计?请把方案画在图3中,并求此时三条小路的总长.
(3)请你探究出一种一般方法,使得出口D不论在什么位置,都能准确地找到另外两个出口E、F的位置,请写明这个方法.
(4)你在(3)中探究出的一般方法适用于正五边形吗?请结合图5予以说明,这种方法能推广到正n边形吗?
参考答案
一.1.B;由对称性知(3,-2).
2.B;提示:2+3=5,两圆半径等于圆心距.
3.C;提示:连OB、OC.
4.B;设圆的半径为R,由3×4=(R-2)(2R-2),R=4.
5.B;提示:由PA·PB=PC·PD.
6.C;直径所对的圆周角是直角.
7.B;转化为解直角三角形问.
8.D;圆内接正六边形的边长等于半径.
9.C;根据闪形面积公式.
10.A;两圆内切.
二.11.26寸; 12、正五边形; 13、一条或2条3条或4条; 14、60-13π; 15、4个.
三.提示:16、由切线长定理及其勾股定理得,BM=4.
17、2m.
四.18、分析:连结OC,通过求圆心角的度数求解.
解:连结OC,
在Rt△AOB中,∠A=35°,
∴∠B=55°,又∵OC=OB,
∴∠COB=180°-2∠B=70°,∴ 的度数为70°,
∠COD=90°-∠COB=90°-70°=20°,
∴ 的度数为20°.
五.19.提示:证明△PAC≌△PBC.
六、20.提示:(1)过点A作公切线;(2)易证BP与CP垂直;(3)中CQ与BQ不垂直.
七、[分析]:
21.(1)方案1:D,E,F与A,B,C重合,连OD,OE,OF.
方案2:OD,OE,OF分别垂直于AB,BC,AC.
(2)OD//AC,OE//AB,OF//BC, 如图(3),
作OM⊥BC于M,连OB,
∵ΔABC是等边三角形,∴BM=BC=30,且∠OBM=30°,
∴OM=10,
∵OE//AB,∴∠OEM=60°,OE==20,
又OE=OF=OD,∴OE+OF+OD=3OE=60,答:略.
(3)如图(4)方法1:在BC,CA,AB上分别截取BE=CF=AD,连结OD,OE,OF,
方法2:在AB上任取一点D,连OD,逆时针旋转OD120°两次,得E,F.
(4)设M1为A1A2上任一点,在各边上分别取A2M2=A3M3=A4M4=A5M5=A1M1,连OM1……OM5即可,
∴可推广到正n边形.
A
B
10m
8m
PAGE
