2021—2022学年苏科版数学七年级下册9.4.1乘法公式:完全平方公式课后补充习题分层练(Word版含答案)
文档属性
| 名称 | 2021—2022学年苏科版数学七年级下册9.4.1乘法公式:完全平方公式课后补充习题分层练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 320.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 11:49:54 | ||
图片预览




文档简介
9.4.1乘法公式:完全平方公式-课后补充习题分层练
-2021-2022学年七年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、计算:(a+1)2﹣a2=_____.
A2、设(5a+3b)2=(5a-3b)2+A,则A等于( )
A.60ab B.30ab C.15ab D.12ab
A3、如果m2+m=5,那么代数式m(m﹣2)+(m+2)2的值为( )
A.14 B.9 C.﹣1 D.﹣6
A4、若是关于的完全平方式,则__________.
A5、若m+=3,则m2+=_____.
A6、已知a2+2a+b2-6b+10=0,那么a=_______,b=______.
A7、若,满足,,则______.
A8、运用完全平方公式计算:
(1)(﹣2a+3)2; (2)(﹣3x+)2, (3)(﹣x2﹣4y)2; (4)(1﹣2b)2.
A9、(2021·全国八年级课时练习)计算:
(1); (2); (3);
(4); (5); (6).
A10、已知:x+y=5,xy=3.求:①x2+5xy+y2;②x4+y4.
【B培优综合】
B11、若代数式可化为,则的值是________.
B12、如果,且,则的值是 ____ .
B13、已知(2019﹣a)2+(a﹣2017)2=7,则代数式(2019﹣a)(a﹣2017)的值是_____.
B14、已知,,则=_____________.
B15、阅读理解.
因为, ①
因为 ②
所以由①得: , 由②得:
所以
试根据上面公式的变形解答下列问题:
(1)已知,则下列等式成立的是( )
①; ②; ③; ④;
A.①; B.①②; C.①②③; D.①②③④;
(2)已知,求下列代数式的值:
①; ②; ③.
B16、(2021秋 西城区期末)(1)如果(x﹣3)(x+2)=x2+mx+n,那么m的值是 ,n的值是 ;
(2)如果(x+a)(x+b)=x2﹣2x+,
①求(a﹣2)(b﹣2)的值; ②求的值.
【C拔尖拓展】
C17、(2021春 蜀山区校级期中)(阅读理解)“若x满足(70﹣x)(x﹣20)=30,
求(70﹣x)2+(x﹣20)2的值”.
解:设(70﹣x)=a,(x﹣20)=b,
则(70﹣x)(x﹣20)=ab=30,a+b=(70﹣x)+(x﹣20)=50,
那么(70﹣x)2+(x﹣20)2=a2+b2=(a+b)2﹣2ab=502﹣2×30=2440.
(解决问题)(1)若x满足(40﹣x)(x﹣10)=﹣10,求(40﹣x)2+(x﹣10)2的值;
(2)若x满足(2021﹣x)2+(2020﹣x)2=4321,求(2021﹣x)(2020﹣x)的值.
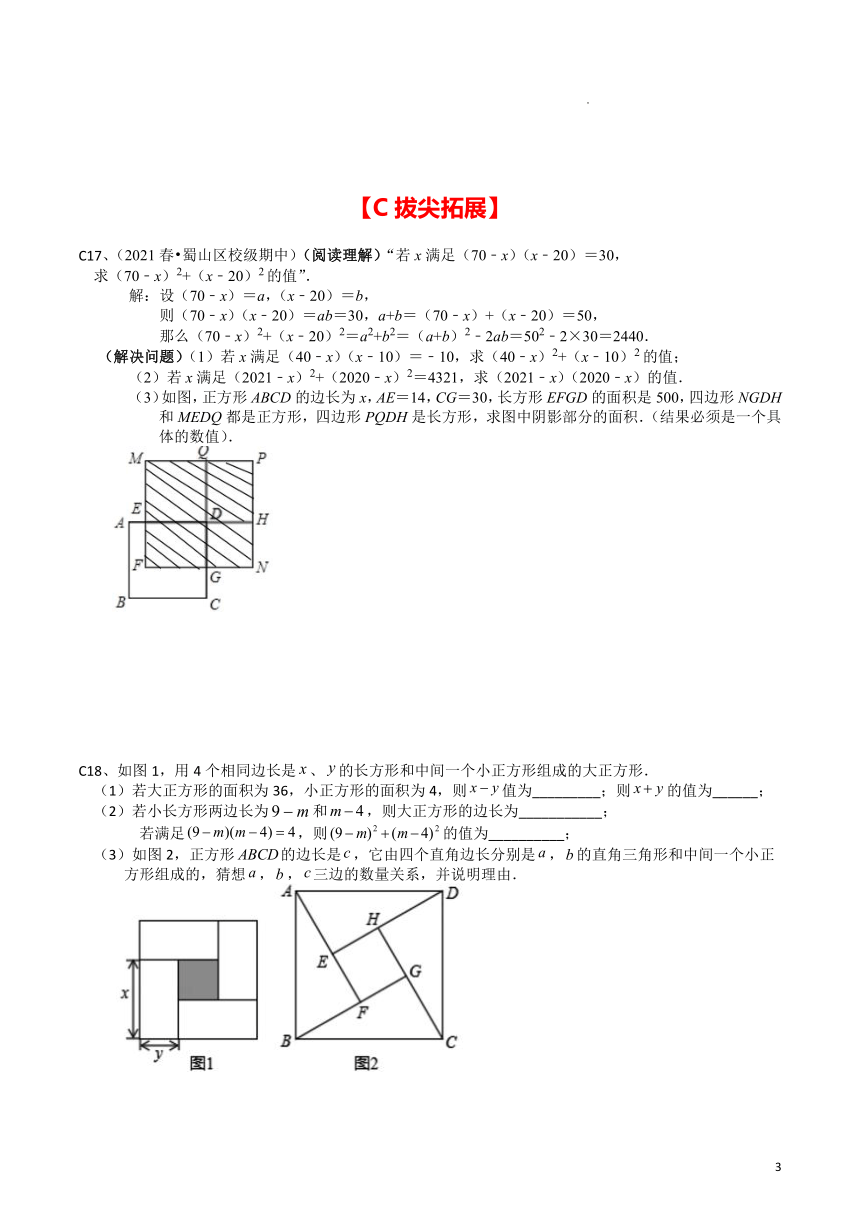
(3)如图,正方形ABCD的边长为x,AE=14,CG=30,长方形EFGD的面积是500,四边形NGDH和MEDQ都是正方形,四边形PQDH是长方形,求图中阴影部分的面积.(结果必须是一个具体的数值).
C18、如图1,用4个相同边长是、的长方形和中间一个小正方形组成的大正方形.
(1)若大正方形的面积为36,小正方形的面积为4,则值为_________;则的值为______;
(2)若小长方形两边长为和,则大正方形的边长为___________;
若满足,则的值为__________;
(3)如图2,正方形的边长是,它由四个直角边长分别是,的直角三角形和中间一个小正方形组成的,猜想,,三边的数量关系,并说明理由.
9.4.1乘法公式:完全平方公式-课后补充习题分层练
-2021-2022学年七年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、计算:(a+1)2﹣a2=_____.
【答案】2a+1
【分析】原式利用完全平方公式展开,然后合并同类项即可得到结果.
【详解】(a+1)2﹣a2=a2+2a+1﹣a2=2a+1,
故答案为2a+1.
A2、设(5a+3b)2=(5a-3b)2+A,则A等于( )
A.60ab B.30ab C.15ab D.12ab
【分析】
根据完全平方公式的展开法则,将等号两边去掉括号,即可得出A.
【详解】
∵(5a+3b)2=(5a-3b)2+A
∴25a2+30ab+9b2=25a2-30ab+9b2+A
∴A=60ab
故选:A
A3、如果m2+m=5,那么代数式m(m﹣2)+(m+2)2的值为( )
A.14 B.9 C.﹣1 D.﹣6
解:m(m﹣2)+(m+2)2
=m2﹣2m+m2+4m+4
=2m2+2m+4.
当m2+m=5时,原式=2(m2+m)+4=2×5+4=10+4=14.
故选:A.
A4、若是关于的完全平方式,则__________.
【答案】7或-1
【分析】直接利用完全平方公式的定义得出2(m-3)=±8,进而求出答案.
详解:∵x2+2(m-3)x+16是关于x的完全平方式,
∴2(m-3)=±8,
解得:m=-1或7,
故答案为-1或7.
A5、若m+=3,则m2+=_____.
【答案】7
【详解】
分析:把已知等式两边平方,利用完全平方公式化简,即可求出答案.
详解:把m+=3两边平方得:(m+)2=m2++2=9,
则m2+=7,
故答案为7
A6、已知a2+2a+b2-6b+10=0,那么a=_______,b=______.
【答案】-13
【解析】
【详解】
∵a2+2a+b2-6b+10=0,
∴a2+2a+1+b2-6b+9=0,
∴(a+1)2+(b﹣3)2=0,
则a+1=0,b﹣3=0,
即a=﹣1,b=3.
故答案为﹣1;3.
A7、若,满足,,则______.
【答案】
【分析】
根据完全平方公式即可求出结论.
【详解】
解:∵,,
∴=20-2×3=14
故答案为:14.
A8、运用完全平方公式计算:
(1)(﹣2a+3)2; (2)(﹣3x+)2, (3)(﹣x2﹣4y)2; (4)(1﹣2b)2.
【分析】(1)利用完全平方公式得到原式=(﹣2a)2+2×(﹣2a)×3+32,然后整理即可;
(2)利用完全平方公式得到原式=(﹣3x)2+2×(﹣3x)×+()2,然后整理即可;
(3)利用完全平方公式得到原式=(﹣x2)2+2×(﹣x2)×(﹣4y)+(﹣4y)2,然后整理即可;
(4)直接利用完全平方公式计算.
【解析】(1)原式=(﹣2a)2+2×(﹣2a)×3+32=4a2﹣12a+9;
(2)原式=(﹣3x)2+2×(﹣3x)×+()2=9x2﹣3x+;
(3)原式=(﹣x2)2+2×(﹣x2)×(﹣4y)+(﹣4y)2=x4+8x2y+16y2;
(4)原式=1﹣4b+4b2.
A9、(2021·全国八年级课时练习)计算:
(1); (2); (3);
(4); (5); (6).
【答案】(1);(2);(3);(4);(5);(6)
【分析】(1)根据完全平方公式: 进行求解即可;
(2)根据完全平方公式: 进行求解即可;
(3)根据完全平方公式: 进行求解即可;
(4)根据完全平方公式: 进行求解即可;
(5)根据完全平方公式: 进行求解即可;
(6)根据完全平方公式: 和平方差公式进行求解即可.
【详解】解:(1);
(2);
(3);
(4),;
(5);
(6)..
A10、已知:x+y=5,xy=3.求:①x2+5xy+y2;②x4+y4.
解:①∵x+y=5,xy=3,
∴x2+5xy+y2=(x+y)2+3xy=52+3×3=34;
②∵x+y=5,xy=3,
∴x2+y2=(x+y)2﹣2xy=52﹣2×3=19,
∴x4+y4=(x2+y2)2﹣2x2y2=192﹣2×32=343.
【B培优综合】
B11、若代数式可化为,则的值是________.
【答案】5
【解析】
,根据题意得,,解得=3,b=8,那么=5.
B12、如果,且,则的值是 ____ .
【答案】1
【详解】
因为(x+n)2=x2+2nx+n2,m>0,所以2n>0,n2=1,所以n=1.
故答案为1.
B13、已知(2019﹣a)2+(a﹣2017)2=7,则代数式(2019﹣a)(a﹣2017)的值是_____.
【答案】
【分析】
根据完全平方公式的变式:ab= 利用整体代入的思想求解即可.
【详解】
解:∵(2019﹣a)2+(a﹣2017)2=7,
∴(2019﹣a)(a﹣2017)={[(2019﹣a)+(a﹣2017)]2﹣[(2019﹣a)2+(a﹣2017)2]}=,
故答案为.
B14、已知,,则=_____________.
【答案】28或36.
【详解】
解:∵,∴ab=±2.
①当a+b=8,ab=2时,==﹣2×2=28;
②当a+b=8,ab=﹣2时,==﹣2×(﹣2)=36;
故答案为28或36.
B15、阅读理解.
因为, ①
因为 ②
所以由①得: , 由②得:
所以
试根据上面公式的变形解答下列问题:
(1)已知,则下列等式成立的是( )
①; ②; ③; ④;
A.①; B.①②; C.①②③; D.①②③④;
(2)已知,求下列代数式的值:
①; ②; ③.
【答案】(1)C;(2)①2;②0;③2
【详解】
(1)
∴
∴
同理:
由两边同时减去2,得:,∴,故选C.
(2)①原式=(a+)2-2=(-2)2-2=2
②原式=a2+-2=2-2=0
③原式=( a2+)2-2=(2)2-2=2
B16、(2021秋 西城区期末)(1)如果(x﹣3)(x+2)=x2+mx+n,那么m的值是 ,n的值是 ;
(2)如果(x+a)(x+b)=x2﹣2x+,
①求(a﹣2)(b﹣2)的值; ②求的值.
【分析】(1)先去括号,合并同类项,根据等式的恒等性,列等式,计算;
(2)先去括号,合并同类项,根据等式的恒等性,求出(a+b)、ab的值,①把(a+b)、ab的值代入整理后的整式计算即可;
②通分后,配方,再把(a+b)、ab的值代入后计算.
【详解】解:(1)∵(x﹣3)(x+2)=x2+mx+n,
∴x2﹣x﹣6=x2+mx+n,
∴m=﹣1,n=﹣6,
故答案为:﹣1,﹣6;
(2)∵,
∴a+b=﹣2,,
①(a﹣2)(b﹣2)=ab﹣2(a+b)+4==,
②====13.
【C拔尖拓展】
C17、(2021春 蜀山区校级期中)(阅读理解)“若x满足(70﹣x)(x﹣20)=30,
求(70﹣x)2+(x﹣20)2的值”.
解:设(70﹣x)=a,(x﹣20)=b,
则(70﹣x)(x﹣20)=ab=30,a+b=(70﹣x)+(x﹣20)=50,
那么(70﹣x)2+(x﹣20)2=a2+b2=(a+b)2﹣2ab=502﹣2×30=2440.
(解决问题)(1)若x满足(40﹣x)(x﹣10)=﹣10,求(40﹣x)2+(x﹣10)2的值;
(2)若x满足(2021﹣x)2+(2020﹣x)2=4321,求(2021﹣x)(2020﹣x)的值.
(3)如图,正方形ABCD的边长为x,AE=14,CG=30,长方形EFGD的面积是500,四边形NGDH和MEDQ都是正方形,四边形PQDH是长方形,求图中阴影部分的面积.(结果必须是一个具体的数值).
【分析】(1)根据举例进行详解即可;
(2)设2021﹣x=c,2020﹣x=d,则可得c2+d2=(2021﹣x)2+(2020﹣x)2=4321,c﹣d=(2021﹣x)﹣(2020﹣x)=1,所以2cd=(c+d)﹣(c﹣d)’,可得cd=2020,2cd=(c2+d2)﹣(c﹣d)2=4320,即可详解;
(3)根据正方形ABCD的边长为x,AE=14,CG=30,所以DE=x﹣14,DG=x﹣30,得到(x﹣14)(x﹣30)=500,设x﹣14=a,x﹣30=b,从而得到ab=500,a﹣b=(x﹣14)﹣(x﹣30)=16,根据举例求出(a+b)2,即可求出阴影部分的面积.
【详解】解:(1)设(40﹣x)=m,(x﹣10)=n,
∴(40﹣x)(x﹣10)=mm=﹣10,m+n=(40﹣x)+(x﹣10)=30,
∴(40﹣x)2+(x﹣10)2=m2+n2=(m+n)2﹣2mm=302﹣2×(﹣10)=920;
(2)设2021﹣x=c,2020﹣x=d,
∴c2+d2=(2021﹣x)2+(2020﹣x)2=4321, c﹣d=(201﹣x)﹣(2020﹣x)=1,
∴2cd=(c2+d2)﹣(c﹣d)2=4320,
∴cd=2160,即(2021﹣x)(2020﹣x)=2160.
(3)∵正方形ABCD的边长为x,AF=14,CG=30,
∴DE=x﹣14,DG=x﹣30, ∴(x﹣14)×(x﹣30)=500,
设x﹣14=a,x﹣30=b,
∴ab=500,a﹣b=(x﹣14)﹣(x﹣30=16,
(a+b)2=(a﹣b)2+4ab=162+4x500=2256,
∴阴影部分的面积为:2256.
C18、如图1,用4个相同边长是、的长方形和中间一个小正方形组成的大正方形.
(1)若大正方形的面积为36,小正方形的面积为4,则值为_________;则的值为______;
(2)若小长方形两边长为和,则大正方形的边长为___________;
若满足,则的值为__________;
(3)如图2,正方形的边长是,它由四个直角边长分别是,的直角三角形和中间一个小正方形组成的,猜想,,三边的数量关系,并说明理由.
【答案】(1)2,6;(2)5,17;(3),理由见解析
【分析】本题考查完全平方公式的几何背景,理清各个图形面积之间的关系是解决问题的关键,用代数式表示各个部分的面积是得出结论的前提.
(1)大正方形的边长为x+y,小正方的边长为x-y,由面积可求出正方形的边长;
(2)小长方形两边之和为正方形的边长,再由完全平方公式求解即可;
(3)根据大、小正方形和4个直角三角形的面积之间的关系得出结论.
解:(1)∵大正方形的面积为36,小正方形的面积为4,
∴,,
又∵,∴,,
故答案为:2,6;
(2)大正方形的边长为,
∵,
∴,
故答案为:5,17;
(3),,三边的数量关系为.
理由如下:由拼图可得,小正方形的边长为,
由大正方形的面积等于小正方形的面积与4个直角三角形的面积和可得,
,即.
(
1
)
学
-2021-2022学年七年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、计算:(a+1)2﹣a2=_____.
A2、设(5a+3b)2=(5a-3b)2+A,则A等于( )
A.60ab B.30ab C.15ab D.12ab
A3、如果m2+m=5,那么代数式m(m﹣2)+(m+2)2的值为( )
A.14 B.9 C.﹣1 D.﹣6
A4、若是关于的完全平方式,则__________.
A5、若m+=3,则m2+=_____.
A6、已知a2+2a+b2-6b+10=0,那么a=_______,b=______.
A7、若,满足,,则______.
A8、运用完全平方公式计算:
(1)(﹣2a+3)2; (2)(﹣3x+)2, (3)(﹣x2﹣4y)2; (4)(1﹣2b)2.
A9、(2021·全国八年级课时练习)计算:
(1); (2); (3);
(4); (5); (6).
A10、已知:x+y=5,xy=3.求:①x2+5xy+y2;②x4+y4.
【B培优综合】
B11、若代数式可化为,则的值是________.
B12、如果,且,则的值是 ____ .
B13、已知(2019﹣a)2+(a﹣2017)2=7,则代数式(2019﹣a)(a﹣2017)的值是_____.
B14、已知,,则=_____________.
B15、阅读理解.
因为, ①
因为 ②
所以由①得: , 由②得:
所以
试根据上面公式的变形解答下列问题:
(1)已知,则下列等式成立的是( )
①; ②; ③; ④;
A.①; B.①②; C.①②③; D.①②③④;
(2)已知,求下列代数式的值:
①; ②; ③.
B16、(2021秋 西城区期末)(1)如果(x﹣3)(x+2)=x2+mx+n,那么m的值是 ,n的值是 ;
(2)如果(x+a)(x+b)=x2﹣2x+,
①求(a﹣2)(b﹣2)的值; ②求的值.
【C拔尖拓展】
C17、(2021春 蜀山区校级期中)(阅读理解)“若x满足(70﹣x)(x﹣20)=30,
求(70﹣x)2+(x﹣20)2的值”.
解:设(70﹣x)=a,(x﹣20)=b,
则(70﹣x)(x﹣20)=ab=30,a+b=(70﹣x)+(x﹣20)=50,
那么(70﹣x)2+(x﹣20)2=a2+b2=(a+b)2﹣2ab=502﹣2×30=2440.
(解决问题)(1)若x满足(40﹣x)(x﹣10)=﹣10,求(40﹣x)2+(x﹣10)2的值;
(2)若x满足(2021﹣x)2+(2020﹣x)2=4321,求(2021﹣x)(2020﹣x)的值.
(3)如图,正方形ABCD的边长为x,AE=14,CG=30,长方形EFGD的面积是500,四边形NGDH和MEDQ都是正方形,四边形PQDH是长方形,求图中阴影部分的面积.(结果必须是一个具体的数值).
C18、如图1,用4个相同边长是、的长方形和中间一个小正方形组成的大正方形.
(1)若大正方形的面积为36,小正方形的面积为4,则值为_________;则的值为______;
(2)若小长方形两边长为和,则大正方形的边长为___________;
若满足,则的值为__________;
(3)如图2,正方形的边长是,它由四个直角边长分别是,的直角三角形和中间一个小正方形组成的,猜想,,三边的数量关系,并说明理由.
9.4.1乘法公式:完全平方公式-课后补充习题分层练
-2021-2022学年七年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、计算:(a+1)2﹣a2=_____.
【答案】2a+1
【分析】原式利用完全平方公式展开,然后合并同类项即可得到结果.
【详解】(a+1)2﹣a2=a2+2a+1﹣a2=2a+1,
故答案为2a+1.
A2、设(5a+3b)2=(5a-3b)2+A,则A等于( )
A.60ab B.30ab C.15ab D.12ab
【分析】
根据完全平方公式的展开法则,将等号两边去掉括号,即可得出A.
【详解】
∵(5a+3b)2=(5a-3b)2+A
∴25a2+30ab+9b2=25a2-30ab+9b2+A
∴A=60ab
故选:A
A3、如果m2+m=5,那么代数式m(m﹣2)+(m+2)2的值为( )
A.14 B.9 C.﹣1 D.﹣6
解:m(m﹣2)+(m+2)2
=m2﹣2m+m2+4m+4
=2m2+2m+4.
当m2+m=5时,原式=2(m2+m)+4=2×5+4=10+4=14.
故选:A.
A4、若是关于的完全平方式,则__________.
【答案】7或-1
【分析】直接利用完全平方公式的定义得出2(m-3)=±8,进而求出答案.
详解:∵x2+2(m-3)x+16是关于x的完全平方式,
∴2(m-3)=±8,
解得:m=-1或7,
故答案为-1或7.
A5、若m+=3,则m2+=_____.
【答案】7
【详解】
分析:把已知等式两边平方,利用完全平方公式化简,即可求出答案.
详解:把m+=3两边平方得:(m+)2=m2++2=9,
则m2+=7,
故答案为7
A6、已知a2+2a+b2-6b+10=0,那么a=_______,b=______.
【答案】-13
【解析】
【详解】
∵a2+2a+b2-6b+10=0,
∴a2+2a+1+b2-6b+9=0,
∴(a+1)2+(b﹣3)2=0,
则a+1=0,b﹣3=0,
即a=﹣1,b=3.
故答案为﹣1;3.
A7、若,满足,,则______.
【答案】
【分析】
根据完全平方公式即可求出结论.
【详解】
解:∵,,
∴=20-2×3=14
故答案为:14.
A8、运用完全平方公式计算:
(1)(﹣2a+3)2; (2)(﹣3x+)2, (3)(﹣x2﹣4y)2; (4)(1﹣2b)2.
【分析】(1)利用完全平方公式得到原式=(﹣2a)2+2×(﹣2a)×3+32,然后整理即可;
(2)利用完全平方公式得到原式=(﹣3x)2+2×(﹣3x)×+()2,然后整理即可;
(3)利用完全平方公式得到原式=(﹣x2)2+2×(﹣x2)×(﹣4y)+(﹣4y)2,然后整理即可;
(4)直接利用完全平方公式计算.
【解析】(1)原式=(﹣2a)2+2×(﹣2a)×3+32=4a2﹣12a+9;
(2)原式=(﹣3x)2+2×(﹣3x)×+()2=9x2﹣3x+;
(3)原式=(﹣x2)2+2×(﹣x2)×(﹣4y)+(﹣4y)2=x4+8x2y+16y2;
(4)原式=1﹣4b+4b2.
A9、(2021·全国八年级课时练习)计算:
(1); (2); (3);
(4); (5); (6).
【答案】(1);(2);(3);(4);(5);(6)
【分析】(1)根据完全平方公式: 进行求解即可;
(2)根据完全平方公式: 进行求解即可;
(3)根据完全平方公式: 进行求解即可;
(4)根据完全平方公式: 进行求解即可;
(5)根据完全平方公式: 进行求解即可;
(6)根据完全平方公式: 和平方差公式进行求解即可.
【详解】解:(1);
(2);
(3);
(4),;
(5);
(6)..
A10、已知:x+y=5,xy=3.求:①x2+5xy+y2;②x4+y4.
解:①∵x+y=5,xy=3,
∴x2+5xy+y2=(x+y)2+3xy=52+3×3=34;
②∵x+y=5,xy=3,
∴x2+y2=(x+y)2﹣2xy=52﹣2×3=19,
∴x4+y4=(x2+y2)2﹣2x2y2=192﹣2×32=343.
【B培优综合】
B11、若代数式可化为,则的值是________.
【答案】5
【解析】
,根据题意得,,解得=3,b=8,那么=5.
B12、如果,且,则的值是 ____ .
【答案】1
【详解】
因为(x+n)2=x2+2nx+n2,m>0,所以2n>0,n2=1,所以n=1.
故答案为1.
B13、已知(2019﹣a)2+(a﹣2017)2=7,则代数式(2019﹣a)(a﹣2017)的值是_____.
【答案】
【分析】
根据完全平方公式的变式:ab= 利用整体代入的思想求解即可.
【详解】
解:∵(2019﹣a)2+(a﹣2017)2=7,
∴(2019﹣a)(a﹣2017)={[(2019﹣a)+(a﹣2017)]2﹣[(2019﹣a)2+(a﹣2017)2]}=,
故答案为.
B14、已知,,则=_____________.
【答案】28或36.
【详解】
解:∵,∴ab=±2.
①当a+b=8,ab=2时,==﹣2×2=28;
②当a+b=8,ab=﹣2时,==﹣2×(﹣2)=36;
故答案为28或36.
B15、阅读理解.
因为, ①
因为 ②
所以由①得: , 由②得:
所以
试根据上面公式的变形解答下列问题:
(1)已知,则下列等式成立的是( )
①; ②; ③; ④;
A.①; B.①②; C.①②③; D.①②③④;
(2)已知,求下列代数式的值:
①; ②; ③.
【答案】(1)C;(2)①2;②0;③2
【详解】
(1)
∴
∴
同理:
由两边同时减去2,得:,∴,故选C.
(2)①原式=(a+)2-2=(-2)2-2=2
②原式=a2+-2=2-2=0
③原式=( a2+)2-2=(2)2-2=2
B16、(2021秋 西城区期末)(1)如果(x﹣3)(x+2)=x2+mx+n,那么m的值是 ,n的值是 ;
(2)如果(x+a)(x+b)=x2﹣2x+,
①求(a﹣2)(b﹣2)的值; ②求的值.
【分析】(1)先去括号,合并同类项,根据等式的恒等性,列等式,计算;
(2)先去括号,合并同类项,根据等式的恒等性,求出(a+b)、ab的值,①把(a+b)、ab的值代入整理后的整式计算即可;
②通分后,配方,再把(a+b)、ab的值代入后计算.
【详解】解:(1)∵(x﹣3)(x+2)=x2+mx+n,
∴x2﹣x﹣6=x2+mx+n,
∴m=﹣1,n=﹣6,
故答案为:﹣1,﹣6;
(2)∵,
∴a+b=﹣2,,
①(a﹣2)(b﹣2)=ab﹣2(a+b)+4==,
②====13.
【C拔尖拓展】
C17、(2021春 蜀山区校级期中)(阅读理解)“若x满足(70﹣x)(x﹣20)=30,
求(70﹣x)2+(x﹣20)2的值”.
解:设(70﹣x)=a,(x﹣20)=b,
则(70﹣x)(x﹣20)=ab=30,a+b=(70﹣x)+(x﹣20)=50,
那么(70﹣x)2+(x﹣20)2=a2+b2=(a+b)2﹣2ab=502﹣2×30=2440.
(解决问题)(1)若x满足(40﹣x)(x﹣10)=﹣10,求(40﹣x)2+(x﹣10)2的值;
(2)若x满足(2021﹣x)2+(2020﹣x)2=4321,求(2021﹣x)(2020﹣x)的值.
(3)如图,正方形ABCD的边长为x,AE=14,CG=30,长方形EFGD的面积是500,四边形NGDH和MEDQ都是正方形,四边形PQDH是长方形,求图中阴影部分的面积.(结果必须是一个具体的数值).
【分析】(1)根据举例进行详解即可;
(2)设2021﹣x=c,2020﹣x=d,则可得c2+d2=(2021﹣x)2+(2020﹣x)2=4321,c﹣d=(2021﹣x)﹣(2020﹣x)=1,所以2cd=(c+d)﹣(c﹣d)’,可得cd=2020,2cd=(c2+d2)﹣(c﹣d)2=4320,即可详解;
(3)根据正方形ABCD的边长为x,AE=14,CG=30,所以DE=x﹣14,DG=x﹣30,得到(x﹣14)(x﹣30)=500,设x﹣14=a,x﹣30=b,从而得到ab=500,a﹣b=(x﹣14)﹣(x﹣30)=16,根据举例求出(a+b)2,即可求出阴影部分的面积.
【详解】解:(1)设(40﹣x)=m,(x﹣10)=n,
∴(40﹣x)(x﹣10)=mm=﹣10,m+n=(40﹣x)+(x﹣10)=30,
∴(40﹣x)2+(x﹣10)2=m2+n2=(m+n)2﹣2mm=302﹣2×(﹣10)=920;
(2)设2021﹣x=c,2020﹣x=d,
∴c2+d2=(2021﹣x)2+(2020﹣x)2=4321, c﹣d=(201﹣x)﹣(2020﹣x)=1,
∴2cd=(c2+d2)﹣(c﹣d)2=4320,
∴cd=2160,即(2021﹣x)(2020﹣x)=2160.
(3)∵正方形ABCD的边长为x,AF=14,CG=30,
∴DE=x﹣14,DG=x﹣30, ∴(x﹣14)×(x﹣30)=500,
设x﹣14=a,x﹣30=b,
∴ab=500,a﹣b=(x﹣14)﹣(x﹣30=16,
(a+b)2=(a﹣b)2+4ab=162+4x500=2256,
∴阴影部分的面积为:2256.
C18、如图1,用4个相同边长是、的长方形和中间一个小正方形组成的大正方形.
(1)若大正方形的面积为36,小正方形的面积为4,则值为_________;则的值为______;
(2)若小长方形两边长为和,则大正方形的边长为___________;
若满足,则的值为__________;
(3)如图2,正方形的边长是,它由四个直角边长分别是,的直角三角形和中间一个小正方形组成的,猜想,,三边的数量关系,并说明理由.
【答案】(1)2,6;(2)5,17;(3),理由见解析
【分析】本题考查完全平方公式的几何背景,理清各个图形面积之间的关系是解决问题的关键,用代数式表示各个部分的面积是得出结论的前提.
(1)大正方形的边长为x+y,小正方的边长为x-y,由面积可求出正方形的边长;
(2)小长方形两边之和为正方形的边长,再由完全平方公式求解即可;
(3)根据大、小正方形和4个直角三角形的面积之间的关系得出结论.
解:(1)∵大正方形的面积为36,小正方形的面积为4,
∴,,
又∵,∴,,
故答案为:2,6;
(2)大正方形的边长为,
∵,
∴,
故答案为:5,17;
(3),,三边的数量关系为.
理由如下:由拼图可得,小正方形的边长为,
由大正方形的面积等于小正方形的面积与4个直角三角形的面积和可得,
,即.
(
1
)
学
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
