2021—2022学年人教版八年级数学下册18.2.1 矩形 同步基础练习卷(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.2.1 矩形 同步基础练习卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 121.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 11:51:34 | ||
图片预览


文档简介
《矩形》同步基础练习卷
一、选择题
1.下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分
D.矩形的对角线相等且互相平分
2、一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为( )
A.(2,2) B.(3,2) C.(3,3) D.(2,3)
3.如图,四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:
①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.
则不能使四边形ABCD成为矩形的是( )
A.①②③ B.②③④ C.②⑤⑥ D.④⑤⑥
4.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠1=∠2
5.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
6.四边形不具有稳定性,如图,矩形ABCD当改变内角大小就变成平行四边形ABC'D',若∠D'AB=30°,则平行四边形ABC'D'的面积与矩形ABCD的面积之比是( )
A. B. C. D.1
7.如图,在矩形ABCD中,AB=2,∠AOB=60°,则BD的长为( )
A.4 B.3 C.2 D.2
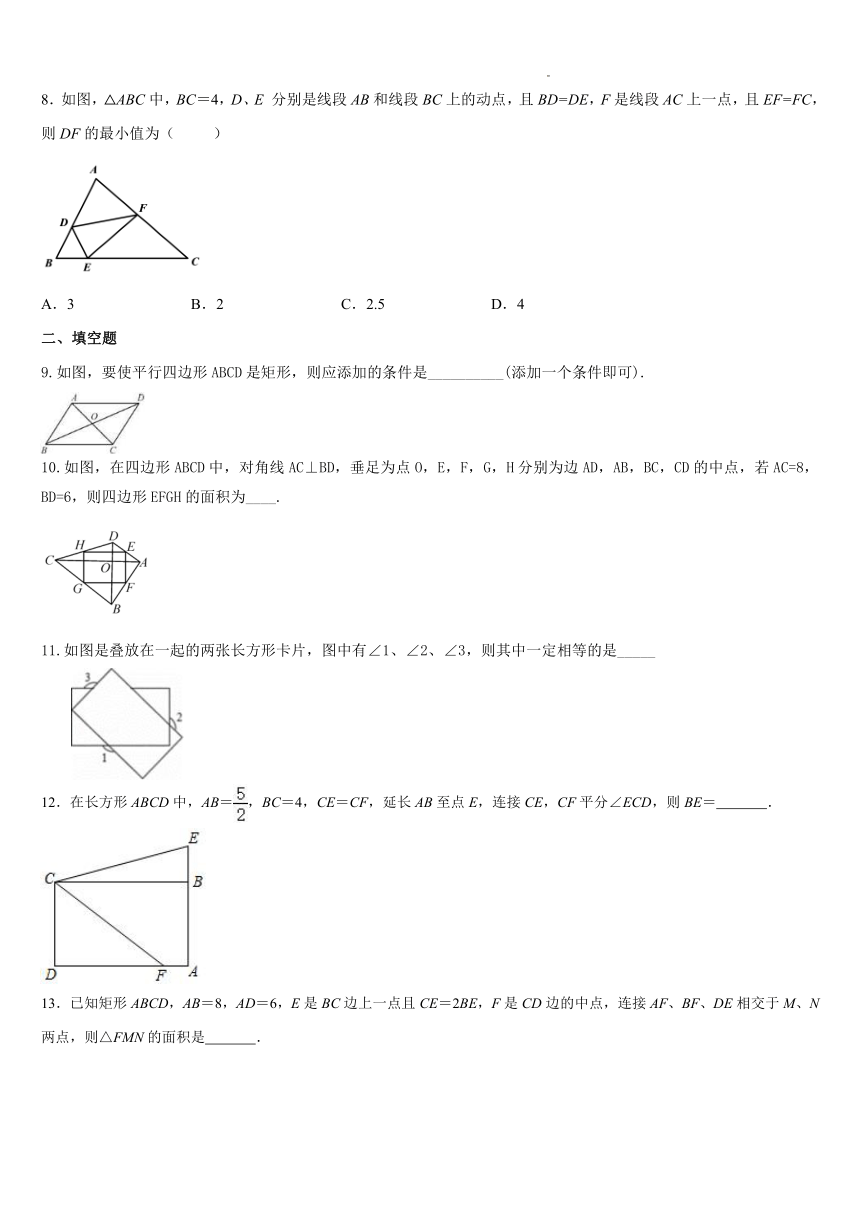
8.如图,△ABC中,BC=4,D、E 分别是线段AB和线段BC上的动点,且BD=DE,F是线段AC上一点,且EF=FC,则DF的最小值为( )
A.3 B.2 C.2.5 D.4
二 、填空题
9.如图,要使平行四边形ABCD是矩形,则应添加的条件是__________(添加一个条件即可).
10.如图,在四边形ABCD中,对角线AC⊥BD,垂足为点O,E,F,G,H分别为边AD,AB,BC,CD的中点,若AC=8,BD=6,则四边形EFGH的面积为____.
11.如图是叠放在一起的两张长方形卡片,图中有∠1、∠2、∠3,则其中一定相等的是_____
12.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE= .
13.已知矩形ABCD,AB=8,AD=6,E是BC边上一点且CE=2BE,F是CD边的中点,连接AF、BF、DE相交于M、N两点,则△FMN的面积是 .
三 、解答题
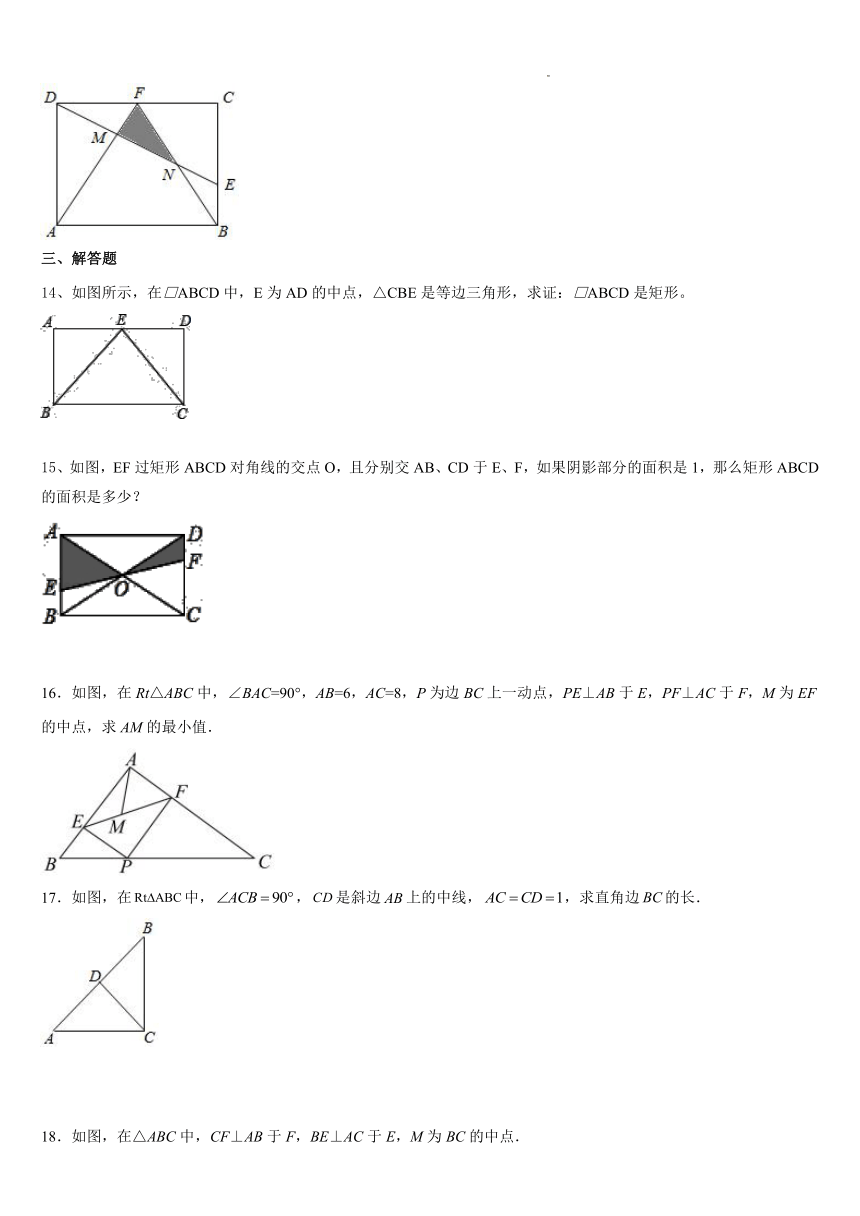
14、如图所示,在□ABCD中,E为AD的中点,△CBE是等边三角形,求证:□ABCD是矩形。
15、如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,如果阴影部分的面积是1,那么矩形ABCD的面积是多少?
16.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,求AM的最小值.
17.如图,在中,,是斜边上的中线,,求直角边的长.
18.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)求证:△MEF是等腰三角形;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
19.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D.点F在BA延长线上,AG平分∠FAC,过D作AB的平行线交AG于点E.求证:四边形ADCE是矩形.
参考答案
1、D 2.B 3.C 4.C 5.C 6.A 7.A 8.B
9.不唯一,如:∠ABC=90°或AC=BD
10.12;
11.∠2=∠3
12:.
13.3.
14、∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,AB=DC,∴∠D+∠A=180°,
∵E是AD边的中点,∴AE=DE,
∵△CBE是等边三角形,∴BE=CE,
在△ABE和△DCE中,AB=DC, AE=DE, BE=CE
∴△ABE≌△DCE(SSS),∴∠A=∠D,
∵∠D+∠A=90°,∴∠D=∠A=90°,∴平行四边形ABCD是矩形.
15. (1)证明:因为AB=AC,
所以∠B=∠ACB,
又因为AD是BC边上的中线,
所以AD⊥BC,即∠ADB=90°.
因为AE∥BC,所以∠EAC=∠ACB,
所以∠B=∠EAC.
因为CE⊥AE,所以∠CEA=90°,
所以∠ADB=∠CEA.
又AB=CA,
所以△ABD≌△CAE(A.A.S.).
(2)解:AB∥DE且AB=DE.
证明:由△ABD≌△CAE可得AE=BD,
又AE∥BD,所以四边形ABDE是平行四边形,所以AB∥DE且AB=DE.
16.证明:∵AC=AB,AD=AE,∠BAD=∠CAE,
∴∠BAD-∠CAB=∠CAE-∠CAB,即∠CAD=∠BAE.
∴△ADC≌△AEB(SAS).
∴DC=BE.
又∵DE=BC,
∴四边形BCDE是平行四边形.
连接BD,CE.
∵AB=AC,AD=AE,∠BAD=∠CAE,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∴四边形BCDE是矩形.
17.解:当F为BC上的中点时,△FDE是等腰三角形,
证明:∵DC⊥DB,F为BC上的中点,
∴DF=0.5BC,
∵BE⊥EC,F为BC上的中点,
∴EF=0.5BC,
∴DF=EF,
∴△FDE是等腰三角形。
18.(1)证明:∵CF⊥AB,BE⊥AC,M为BC的中点,
∴EM=BC,FM=BC,
∴BM=FM,
∴△MEF是等腰三角形;
(2)∵BM=FM,∠ABC=50°,
∴∠MBF=∠MFB=50°,
∴∠BMF=180°﹣2×50°=80°,
∵CM=EM,∠ACB=60°,
∴∠MCE=∠MEC=60°,
∴∠CME=180°﹣2×60°=60°,
∴∠EMF=180°﹣∠BMF﹣∠CME=40°.
19.证明:∵AB=AC,
∴∠B=∠ACB,
∵AE是∠BAC的外角平分线,
∴∠FAE=∠EAC,
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD,
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AEBD,AE=BD,
∵AD⊥BC,AB=AC,
∴BD=DC,
∴AEDC,AE=DC,
故四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
即四边形ADCE是矩形.
一、选择题
1.下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分
D.矩形的对角线相等且互相平分
2、一个长方形在平面直角坐标系中三个顶点的坐标为(﹣1,﹣1),(﹣1,2),(3,﹣1),则第四个顶点的坐标为( )
A.(2,2) B.(3,2) C.(3,3) D.(2,3)
3.如图,四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:
①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.
则不能使四边形ABCD成为矩形的是( )
A.①②③ B.②③④ C.②⑤⑥ D.④⑤⑥
4.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠1=∠2
5.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
6.四边形不具有稳定性,如图,矩形ABCD当改变内角大小就变成平行四边形ABC'D',若∠D'AB=30°,则平行四边形ABC'D'的面积与矩形ABCD的面积之比是( )
A. B. C. D.1
7.如图,在矩形ABCD中,AB=2,∠AOB=60°,则BD的长为( )
A.4 B.3 C.2 D.2
8.如图,△ABC中,BC=4,D、E 分别是线段AB和线段BC上的动点,且BD=DE,F是线段AC上一点,且EF=FC,则DF的最小值为( )
A.3 B.2 C.2.5 D.4
二 、填空题
9.如图,要使平行四边形ABCD是矩形,则应添加的条件是__________(添加一个条件即可).
10.如图,在四边形ABCD中,对角线AC⊥BD,垂足为点O,E,F,G,H分别为边AD,AB,BC,CD的中点,若AC=8,BD=6,则四边形EFGH的面积为____.
11.如图是叠放在一起的两张长方形卡片,图中有∠1、∠2、∠3,则其中一定相等的是_____
12.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE= .
13.已知矩形ABCD,AB=8,AD=6,E是BC边上一点且CE=2BE,F是CD边的中点,连接AF、BF、DE相交于M、N两点,则△FMN的面积是 .
三 、解答题
14、如图所示,在□ABCD中,E为AD的中点,△CBE是等边三角形,求证:□ABCD是矩形。
15、如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,如果阴影部分的面积是1,那么矩形ABCD的面积是多少?
16.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,求AM的最小值.
17.如图,在中,,是斜边上的中线,,求直角边的长.
18.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)求证:△MEF是等腰三角形;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
19.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D.点F在BA延长线上,AG平分∠FAC,过D作AB的平行线交AG于点E.求证:四边形ADCE是矩形.
参考答案
1、D 2.B 3.C 4.C 5.C 6.A 7.A 8.B
9.不唯一,如:∠ABC=90°或AC=BD
10.12;
11.∠2=∠3
12:.
13.3.
14、∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,AB=DC,∴∠D+∠A=180°,
∵E是AD边的中点,∴AE=DE,
∵△CBE是等边三角形,∴BE=CE,
在△ABE和△DCE中,AB=DC, AE=DE, BE=CE
∴△ABE≌△DCE(SSS),∴∠A=∠D,
∵∠D+∠A=90°,∴∠D=∠A=90°,∴平行四边形ABCD是矩形.
15. (1)证明:因为AB=AC,
所以∠B=∠ACB,
又因为AD是BC边上的中线,
所以AD⊥BC,即∠ADB=90°.
因为AE∥BC,所以∠EAC=∠ACB,
所以∠B=∠EAC.
因为CE⊥AE,所以∠CEA=90°,
所以∠ADB=∠CEA.
又AB=CA,
所以△ABD≌△CAE(A.A.S.).
(2)解:AB∥DE且AB=DE.
证明:由△ABD≌△CAE可得AE=BD,
又AE∥BD,所以四边形ABDE是平行四边形,所以AB∥DE且AB=DE.
16.证明:∵AC=AB,AD=AE,∠BAD=∠CAE,
∴∠BAD-∠CAB=∠CAE-∠CAB,即∠CAD=∠BAE.
∴△ADC≌△AEB(SAS).
∴DC=BE.
又∵DE=BC,
∴四边形BCDE是平行四边形.
连接BD,CE.
∵AB=AC,AD=AE,∠BAD=∠CAE,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∴四边形BCDE是矩形.
17.解:当F为BC上的中点时,△FDE是等腰三角形,
证明:∵DC⊥DB,F为BC上的中点,
∴DF=0.5BC,
∵BE⊥EC,F为BC上的中点,
∴EF=0.5BC,
∴DF=EF,
∴△FDE是等腰三角形。
18.(1)证明:∵CF⊥AB,BE⊥AC,M为BC的中点,
∴EM=BC,FM=BC,
∴BM=FM,
∴△MEF是等腰三角形;
(2)∵BM=FM,∠ABC=50°,
∴∠MBF=∠MFB=50°,
∴∠BMF=180°﹣2×50°=80°,
∵CM=EM,∠ACB=60°,
∴∠MCE=∠MEC=60°,
∴∠CME=180°﹣2×60°=60°,
∴∠EMF=180°﹣∠BMF﹣∠CME=40°.
19.证明:∵AB=AC,
∴∠B=∠ACB,
∵AE是∠BAC的外角平分线,
∴∠FAE=∠EAC,
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD,
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AEBD,AE=BD,
∵AD⊥BC,AB=AC,
∴BD=DC,
∴AEDC,AE=DC,
故四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
即四边形ADCE是矩形.
