北师大版七年级数学下册 2.2 探索平行线的性质(一) 教案+学案+练习题(无答案)
文档属性
| 名称 | 北师大版七年级数学下册 2.2 探索平行线的性质(一) 教案+学案+练习题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 321.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 14:57:24 | ||
图片预览


文档简介
平行线的性质(一)
[教学目标]:
1、经历观察、操作、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达的能力。
2、经历探索平行线性质的过程,掌握平行线的特征,并能解决一些问题。
[教学重点]平行线的性质的探索。
[教学难点]运用平行线的特征进行有条理的分析、表达;明确平行线的性质和判定的区别。
[设计理念]为学生提供充足的探索与交流的时间和空间,重视学生在实际操作以及在操作过程中的思考,使学生的空间观念、推理能力得到培养。
[教学方法] 目标教学法
[教学过程]
一、 复习回顾:两直线平行的判定:
同位角 ,两直线平行 两直线平行,同位角
内位角 ,两直线平行 两直线平行,内位角
同旁内角 ,两直线平行 两直线平行,同旁内角
二、学习目标展示(见课件)
三、目标导学
探索一:
实验验证,探索特征
已知,a//b,任意画一条直线c与平行线a、b相交。任选一对同位角、内错角、同旁内角,用适当的方法实验,看看这这些角有什么关系?
(要求学生多画几条截线试试,鼓励学生用多种方法进行探索)
结论:若两条平行线被第三条直线所截,则有:
性质1:两直线平行, .
性质2:两直线平行, .
性质3:两直线平行,
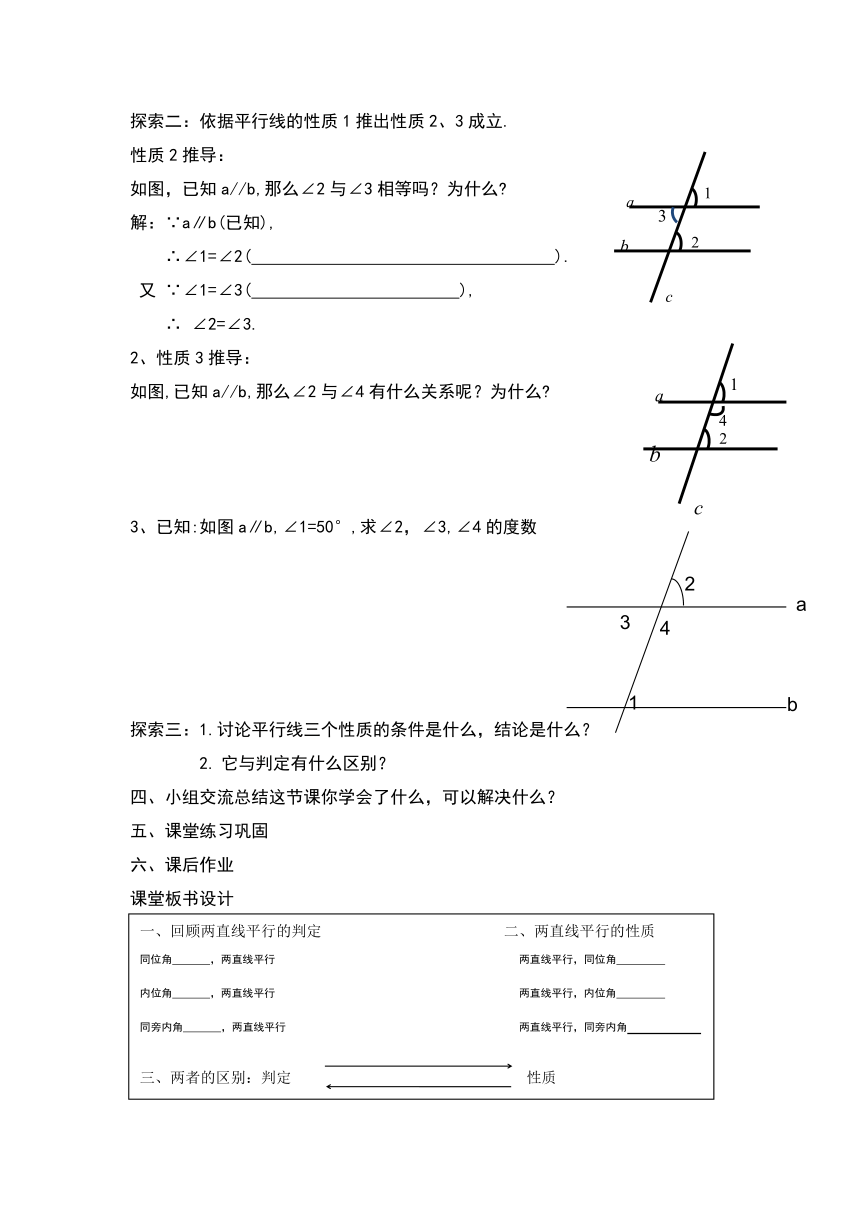
探索二:依据平行线的性质1推出性质2、3成立.
性质2推导:
如图,已知a//b,那么∠2与∠3相等吗?为什么
解:∵a∥b(已知),
∴∠1=∠2( ).
又 ∵∠1=∠3( ),
∴ ∠2=∠3.
2、性质3推导:
如图,已知a//b,那么∠2与∠4有什么关系呢?为什么
3、已知:如图a∥b,∠1=50°,求∠2,∠3,∠4的度数
探索三:1.讨论平行线三个性质的条件是什么,结论是什么?
它与判定有什么区别?
小组交流总结这节课你学会了什么,可以解决什么?
课堂练习巩固
六、课后作业
课堂板书设计
《平行线的性质》导学案
一、预习重点:探索平行线的性质
复习回顾:两直线平行的判定:
同位角 ,两直线平行
内位角 ,两直线平行
同旁内角 ,两直线平行
二(活动一)、探索两平行直线平行线,被第三条直线所截的性质
任意画两平行直线a、b,被第三条直线c所截,回答下面问题:
1.测量图中角的大小,填进表格
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数
2.它们的大小有什么关系
3.你的结论:
条件 结论 几何语言表示(见上图1)
两直线平行 1. ,
2. ,
3. ,
三(活动二)、探索性质1推导性质2、性质3的过程
性质2推导:
如图,已知a//b,那么 2与 3相等吗?为什么
解:∵a∥b(已知),
∴∠1=∠2( ).
又 ∵∠1=∠3( ),
∴ ∠2=∠3.
性质3推导:
如图,已知a//b,那么∠2与∠4有什么关系呢?为什么
1.归纳:平行线三个性质的条件是什么?结论是什么?
2.它与判定有什么区别?
如图,回答以下问题:
平行线的性质课堂检测题
一、判断题
1.在同一平面内的两条直线被第三条直线所截,那么同位角相等.( )
2.两直线平行,同旁内角相等.( )
二、选择题
1.下面的说法中正确的是( )
A.两条直线被第三条直线所截,同位角相等
B.两条直线被第三条直线所截,内错角相等
C.两条直线被第三条直线所截,同旁内角互补
D.以上都不对
2如图1,若∠1=80 ,a∥b,则∠2的度数是( )
A.100 B.70 C.80 D.60
3.如图2,已知∠1=∠2,∠3=125°,那么∠4的度数为( )
A.45° B.55° C.65° D.75°
4.如图3,已知AB∥DE,∠A=150°,∠D=140°,则∠C的度数是( )
A.60° B.75° C.70° D.50°
三、填空题
1.两条直线被第三条直线所截,如果内错角相等,则同旁内角_________
2.如图4,如果,则;
3.如图5:已知:,则
4.如图6:已知:,则
四、填写推理的理由
1.如图
∵BE平分∠ABC(已知)
∴∠1=∠3( )
又∵∠1=∠2(已知)
∴_________=∠2
∴_________∥_________( )
∴∠AED=________ _( )
2.如图所示 ∠1 =∠2,求证 : ∠3 =∠4
证明:∵ ∠1 =∠2( )
∴a//b( )
∴ ∠3 =∠4( )
倒过来读读
b
1
2
a
c
3
b
1
2
a
c
4
a
b
2
4
3
1
回顾两直线平行的判定 二、两直线平行的性质
同位角 ,两直线平行 两直线平行,同位角
内位角 ,两直线平行 两直线平行,内位角
同旁内角 ,两直线平行 两直线平行,同旁内角
三、两者的区别:判定 性质
c
b
1
2
a
c
a
b
图1
b
1
2
a
c
3
b
1
2
a
c
4
( 已知 )
b
1
2
a
c
3
( )
( 已知 )
( )
图1
图2
图3
图6
图5
图4
c
d
a
b
3
4
2
1
[教学目标]:
1、经历观察、操作、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达的能力。
2、经历探索平行线性质的过程,掌握平行线的特征,并能解决一些问题。
[教学重点]平行线的性质的探索。
[教学难点]运用平行线的特征进行有条理的分析、表达;明确平行线的性质和判定的区别。
[设计理念]为学生提供充足的探索与交流的时间和空间,重视学生在实际操作以及在操作过程中的思考,使学生的空间观念、推理能力得到培养。
[教学方法] 目标教学法
[教学过程]
一、 复习回顾:两直线平行的判定:
同位角 ,两直线平行 两直线平行,同位角
内位角 ,两直线平行 两直线平行,内位角
同旁内角 ,两直线平行 两直线平行,同旁内角
二、学习目标展示(见课件)
三、目标导学
探索一:
实验验证,探索特征
已知,a//b,任意画一条直线c与平行线a、b相交。任选一对同位角、内错角、同旁内角,用适当的方法实验,看看这这些角有什么关系?
(要求学生多画几条截线试试,鼓励学生用多种方法进行探索)
结论:若两条平行线被第三条直线所截,则有:
性质1:两直线平行, .
性质2:两直线平行, .
性质3:两直线平行,
探索二:依据平行线的性质1推出性质2、3成立.
性质2推导:
如图,已知a//b,那么∠2与∠3相等吗?为什么
解:∵a∥b(已知),
∴∠1=∠2( ).
又 ∵∠1=∠3( ),
∴ ∠2=∠3.
2、性质3推导:
如图,已知a//b,那么∠2与∠4有什么关系呢?为什么
3、已知:如图a∥b,∠1=50°,求∠2,∠3,∠4的度数
探索三:1.讨论平行线三个性质的条件是什么,结论是什么?
它与判定有什么区别?
小组交流总结这节课你学会了什么,可以解决什么?
课堂练习巩固
六、课后作业
课堂板书设计
《平行线的性质》导学案
一、预习重点:探索平行线的性质
复习回顾:两直线平行的判定:
同位角 ,两直线平行
内位角 ,两直线平行
同旁内角 ,两直线平行
二(活动一)、探索两平行直线平行线,被第三条直线所截的性质
任意画两平行直线a、b,被第三条直线c所截,回答下面问题:
1.测量图中角的大小,填进表格
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数
2.它们的大小有什么关系
3.你的结论:
条件 结论 几何语言表示(见上图1)
两直线平行 1. ,
2. ,
3. ,
三(活动二)、探索性质1推导性质2、性质3的过程
性质2推导:
如图,已知a//b,那么 2与 3相等吗?为什么
解:∵a∥b(已知),
∴∠1=∠2( ).
又 ∵∠1=∠3( ),
∴ ∠2=∠3.
性质3推导:
如图,已知a//b,那么∠2与∠4有什么关系呢?为什么
1.归纳:平行线三个性质的条件是什么?结论是什么?
2.它与判定有什么区别?
如图,回答以下问题:
平行线的性质课堂检测题
一、判断题
1.在同一平面内的两条直线被第三条直线所截,那么同位角相等.( )
2.两直线平行,同旁内角相等.( )
二、选择题
1.下面的说法中正确的是( )
A.两条直线被第三条直线所截,同位角相等
B.两条直线被第三条直线所截,内错角相等
C.两条直线被第三条直线所截,同旁内角互补
D.以上都不对
2如图1,若∠1=80 ,a∥b,则∠2的度数是( )
A.100 B.70 C.80 D.60
3.如图2,已知∠1=∠2,∠3=125°,那么∠4的度数为( )
A.45° B.55° C.65° D.75°
4.如图3,已知AB∥DE,∠A=150°,∠D=140°,则∠C的度数是( )
A.60° B.75° C.70° D.50°
三、填空题
1.两条直线被第三条直线所截,如果内错角相等,则同旁内角_________
2.如图4,如果,则;
3.如图5:已知:,则
4.如图6:已知:,则
四、填写推理的理由
1.如图
∵BE平分∠ABC(已知)
∴∠1=∠3( )
又∵∠1=∠2(已知)
∴_________=∠2
∴_________∥_________( )
∴∠AED=________ _( )
2.如图所示 ∠1 =∠2,求证 : ∠3 =∠4
证明:∵ ∠1 =∠2( )
∴a//b( )
∴ ∠3 =∠4( )
倒过来读读
b
1
2
a
c
3
b
1
2
a
c
4
a
b
2
4
3
1
回顾两直线平行的判定 二、两直线平行的性质
同位角 ,两直线平行 两直线平行,同位角
内位角 ,两直线平行 两直线平行,内位角
同旁内角 ,两直线平行 两直线平行,同旁内角
三、两者的区别:判定 性质
c
b
1
2
a
c
a
b
图1
b
1
2
a
c
3
b
1
2
a
c
4
( 已知 )
b
1
2
a
c
3
( )
( 已知 )
( )
图1
图2
图3
图6
图5
图4
c
d
a
b
3
4
2
1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
