华师大版数学八下17.3.2.1一次函数的图像及平移规律课件(共26张ppt)
文档属性
| 名称 | 华师大版数学八下17.3.2.1一次函数的图像及平移规律课件(共26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 15:36:25 | ||
图片预览



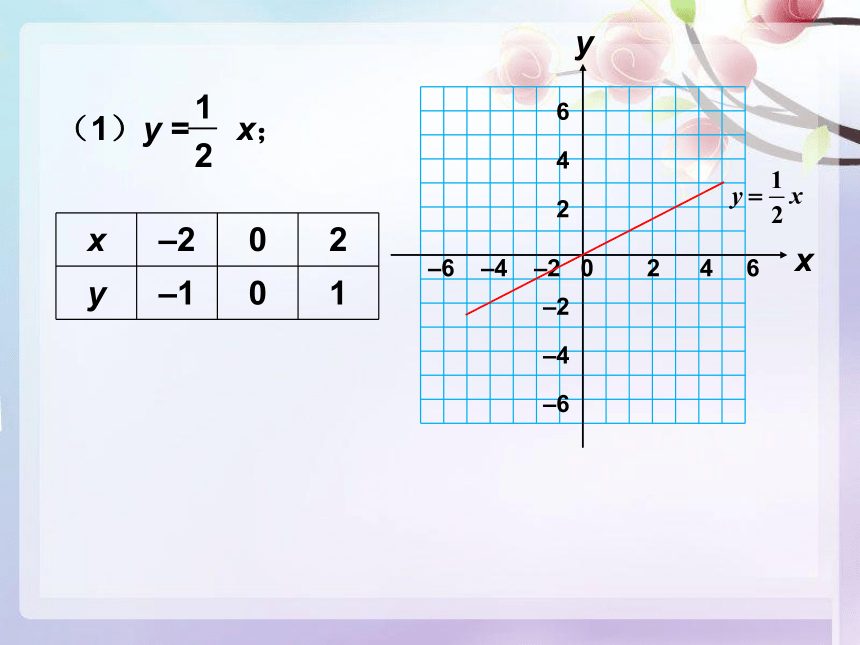
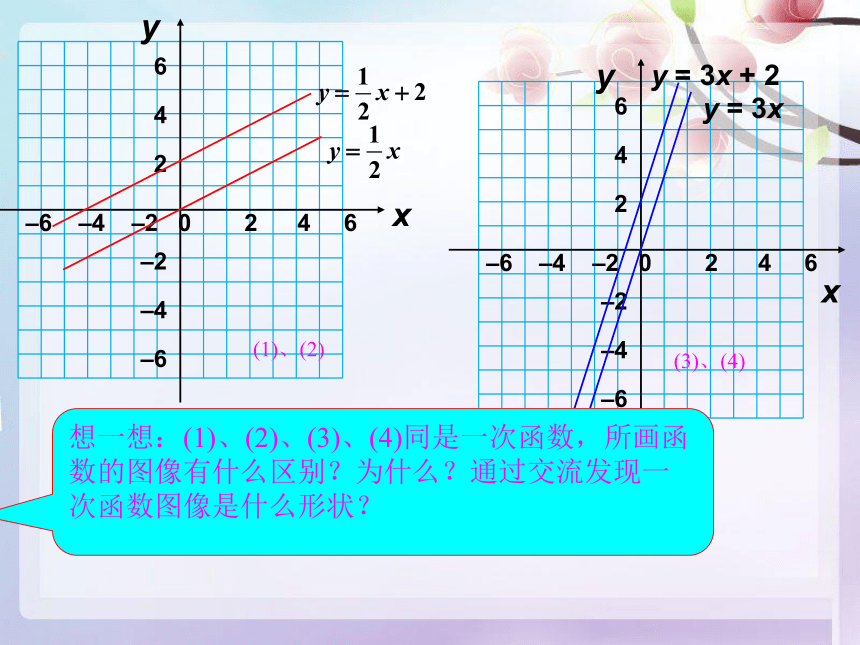
文档简介
(共26张PPT)
第1课时 一次函数的图象及平移规律
华东师大版八年级数学下册
2 一次函数的图象
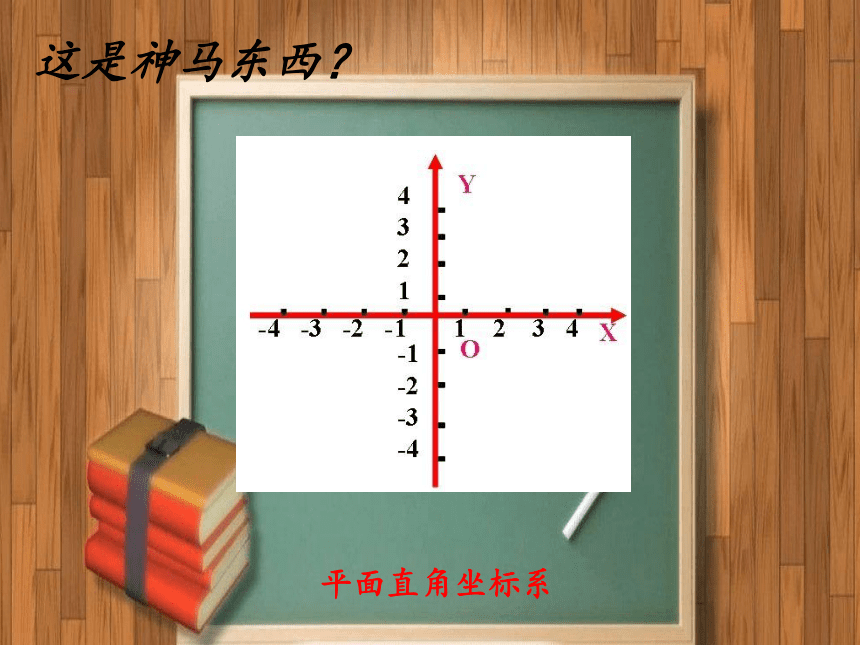
这是神马东西?
平面直角坐标系
A
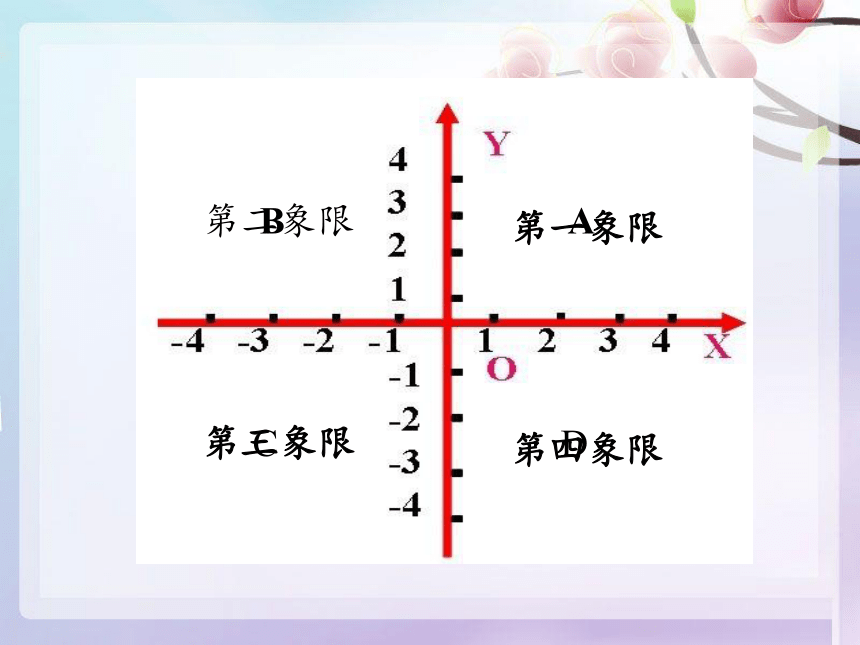
第一象限
B
第二象限
C
第三象限
D
第四象限
(2)y = x + 2;
1
2
(4)y = 3x + 2;
新课探索
做
一
做
在同一平面坐标系中画出下列函数的图象:
(1)y = x;
1
2
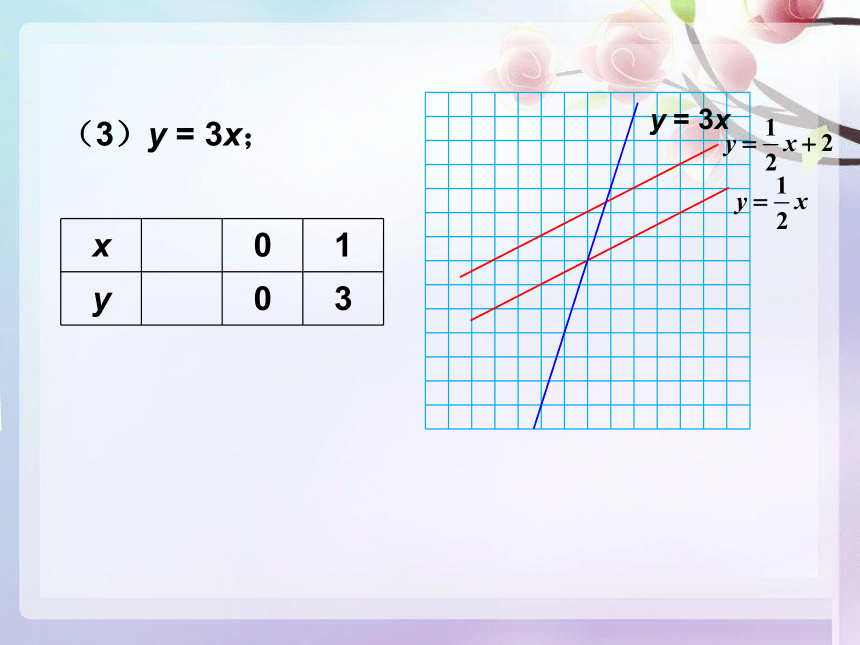
(3)y = 3x;
(1)y = x;
1
2
x –2 0 2
y –1 0 1
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
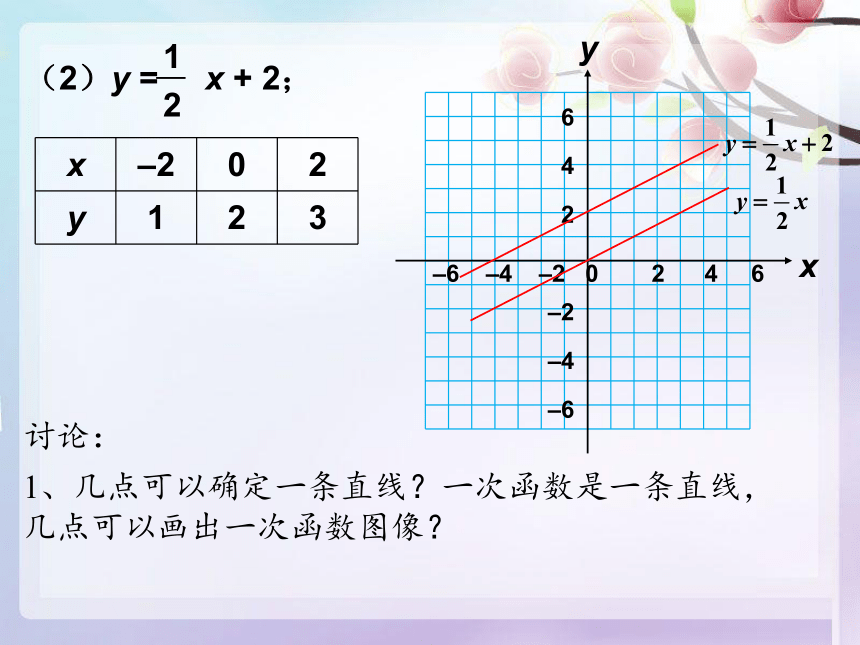
(2)y = x + 2;
1
2
x –2 0 2
y 1 2 3
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
讨论:
1、几点可以确定一条直线?一次函数是一条直线,几点可以画出一次函数图像?
(3)y = 3x;
x 0 1
y 0 3
y = 3x
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
想一想:(1)、(2)、(3)、(4)同是一次函数,所画函数的图像有什么区别?为什么?通过交流发现一次函数图像是什么形状?
(1)、(2)
(3)、(4)
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
(1)、(2)
(3)、(4)
答:1、(1)和(3)的图像经过原点,(2)和(4)图像不过原点,与x、y轴各有一个交点。
2、一次函数图像是一条直线。
一次函数 的图像是一条直线,通常也称为直线 ,特别的,正比例函数 的图像是经过原点 的一条直线。
结论:
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
(1)、(2)
(3)、(4)
讨论:
1、一次函数是一条直线,几点可以画出一次函数图像?
答:两点。
2、取哪几个点可以简单清楚地画出一次函数的图像?
1.正比例函数图过原点,所以可以取 和 任意一点。
2.一次函数与x轴和y轴各交了一点,所以可
取一次函数与y轴和x轴的交点 。
结论:
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(4)y = 3x + 2;
x 0 1
y 2 5
y = 3x
y = 3x + 2
两个一次函数,当系
数 k 相同,b 不相同时(如
y = 3x 与 y = 3x + 2 )有:
共同点:___________
不同点:_______________
两直线平行
与 y 轴交点不同
y = 3x + 2
而当 b 相同,k 不相
同时(如 y = 3x + 2 与 y =
x + 2 )有:
共同点:_________________
不同点:_____________
两直线不平行
与 y 轴交于同一点
1
2
x
y
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(4)y = 3x + 2;
x 0 1
y 2 5
y = 3x
y = 3x + 2
讨论:
1、红色直线代表的函数它们的k有什么特点?从而得到这两条直线的位置关系是什么?
2、蓝色代表的直线同样的结论是否适用?
3、k的值越大与y轴的距离如何?陡峭层度如何?
归纳:
1、k相同,两条直线平行。2、当k>0时,k越大越接近y轴,直线越陡
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
由图看出 y = 3x + 2 可以由 y = 3x 沿 y 轴向上平移 2 个单位得到.
y = x + 2 可以由 y = x 沿 y 轴向上平移 2 个单位得到.
1
2
1
2
在同一平面直角坐标系中画出下列函数的图象,并说出它们有什么关系:
(1)y = – 2x;(2)y = – 2x – 4.
x
y
y = – 2x
y = – 2x 沿 y 轴向下平移 4 个单位得到 y = – 2x – 4.
由正比例函数 y = kx + b 的图象向上平移 h(h > 0)个单位,可得一次函数 y = kx +(b + h)的图象;
由正比例函数 y = kx + b 的图象向下平移 h(h > 0)个单位,可得一次函数 y = kx +(b – h )的图象. 可简记为“上加下减”.
总
结
(1) 函数图像
图像的异 同点?什么因
素影响的?
k相同平行,b不同与y轴的交点不一样,
b=0在原点,
b>0向上平移,
b<0向下平移
(2) 的函数图像
图像的异同点?什么因
素影响的?
k相同平行,b不同与y轴的交点不一样,
b=0在原点,
b>0向上平移,
b<0向下平移
(3) 函数图像:
图像的异同点?什么因素影响的?
当k>0时,k越大,越接近y轴,图像越陡
俗称“一撇
(4) 函数图像:
图像的异同点?什么因素影响的?
当k<0时,k越小,越接近y轴,图像越陡
俗称“一捺”
三、结论:
1、两个一次函数,k相同,b不同时,图像的共同点和不同点有:
共同点:图像直线平行,倾斜度相同;
不同的:与y轴的交点不同,都由函数
图像向上或向下平移得到。
2、两个一次函数,b相同,k不同时,图像的共同点和不同点有:
共同点:图像与Y轴交点相同,都是 ;
不同的:图像不平行, 越大,直线越陡。
3、 时,图像左低右高,俗称“一撇”;
时,图像右高左低,俗称“一捺”。
⑴ 将直线y=3x向下平移2个单位,得到直线________。
⑵ 将直线y=﹣x ﹣5向上平移5个单位,得到直线_____。
y=3x ﹣2
y= ﹣ x
拓展提升
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
y=2x
y=-2x
y=-3x
y=-x
y=3x
y=x
1、(1)观察正比例函数y = - 3x与y = 3x , y = -2 x 与y = 2x, y = -x与y = x 的位置关于 对称,比例系数K的关系是 ;
(2)当 越大时,图象越靠近
y轴。
X轴 、Y轴
互为相反数
|k|
第1课时 一次函数的图象及平移规律
华东师大版八年级数学下册
2 一次函数的图象
这是神马东西?
平面直角坐标系
A
第一象限
B
第二象限
C
第三象限
D
第四象限
(2)y = x + 2;
1
2
(4)y = 3x + 2;
新课探索
做
一
做
在同一平面坐标系中画出下列函数的图象:
(1)y = x;
1
2
(3)y = 3x;
(1)y = x;
1
2
x –2 0 2
y –1 0 1
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(2)y = x + 2;
1
2
x –2 0 2
y 1 2 3
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
讨论:
1、几点可以确定一条直线?一次函数是一条直线,几点可以画出一次函数图像?
(3)y = 3x;
x 0 1
y 0 3
y = 3x
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
想一想:(1)、(2)、(3)、(4)同是一次函数,所画函数的图像有什么区别?为什么?通过交流发现一次函数图像是什么形状?
(1)、(2)
(3)、(4)
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
(1)、(2)
(3)、(4)
答:1、(1)和(3)的图像经过原点,(2)和(4)图像不过原点,与x、y轴各有一个交点。
2、一次函数图像是一条直线。
一次函数 的图像是一条直线,通常也称为直线 ,特别的,正比例函数 的图像是经过原点 的一条直线。
结论:
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
(1)、(2)
(3)、(4)
讨论:
1、一次函数是一条直线,几点可以画出一次函数图像?
答:两点。
2、取哪几个点可以简单清楚地画出一次函数的图像?
1.正比例函数图过原点,所以可以取 和 任意一点。
2.一次函数与x轴和y轴各交了一点,所以可
取一次函数与y轴和x轴的交点 。
结论:
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(4)y = 3x + 2;
x 0 1
y 2 5
y = 3x
y = 3x + 2
两个一次函数,当系
数 k 相同,b 不相同时(如
y = 3x 与 y = 3x + 2 )有:
共同点:___________
不同点:_______________
两直线平行
与 y 轴交点不同
y = 3x + 2
而当 b 相同,k 不相
同时(如 y = 3x + 2 与 y =
x + 2 )有:
共同点:_________________
不同点:_____________
两直线不平行
与 y 轴交于同一点
1
2
x
y
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
(4)y = 3x + 2;
x 0 1
y 2 5
y = 3x
y = 3x + 2
讨论:
1、红色直线代表的函数它们的k有什么特点?从而得到这两条直线的位置关系是什么?
2、蓝色代表的直线同样的结论是否适用?
3、k的值越大与y轴的距离如何?陡峭层度如何?
归纳:
1、k相同,两条直线平行。2、当k>0时,k越大越接近y轴,直线越陡
x
y
–6 –4 –2 0 2 4 6
6
4
2
–2
–4
–6
y = 3x
y = 3x + 2
由图看出 y = 3x + 2 可以由 y = 3x 沿 y 轴向上平移 2 个单位得到.
y = x + 2 可以由 y = x 沿 y 轴向上平移 2 个单位得到.
1
2
1
2
在同一平面直角坐标系中画出下列函数的图象,并说出它们有什么关系:
(1)y = – 2x;(2)y = – 2x – 4.
x
y
y = – 2x
y = – 2x 沿 y 轴向下平移 4 个单位得到 y = – 2x – 4.
由正比例函数 y = kx + b 的图象向上平移 h(h > 0)个单位,可得一次函数 y = kx +(b + h)的图象;
由正比例函数 y = kx + b 的图象向下平移 h(h > 0)个单位,可得一次函数 y = kx +(b – h )的图象. 可简记为“上加下减”.
总
结
(1) 函数图像
图像的异 同点?什么因
素影响的?
k相同平行,b不同与y轴的交点不一样,
b=0在原点,
b>0向上平移,
b<0向下平移
(2) 的函数图像
图像的异同点?什么因
素影响的?
k相同平行,b不同与y轴的交点不一样,
b=0在原点,
b>0向上平移,
b<0向下平移
(3) 函数图像:
图像的异同点?什么因素影响的?
当k>0时,k越大,越接近y轴,图像越陡
俗称“一撇
(4) 函数图像:
图像的异同点?什么因素影响的?
当k<0时,k越小,越接近y轴,图像越陡
俗称“一捺”
三、结论:
1、两个一次函数,k相同,b不同时,图像的共同点和不同点有:
共同点:图像直线平行,倾斜度相同;
不同的:与y轴的交点不同,都由函数
图像向上或向下平移得到。
2、两个一次函数,b相同,k不同时,图像的共同点和不同点有:
共同点:图像与Y轴交点相同,都是 ;
不同的:图像不平行, 越大,直线越陡。
3、 时,图像左低右高,俗称“一撇”;
时,图像右高左低,俗称“一捺”。
⑴ 将直线y=3x向下平移2个单位,得到直线________。
⑵ 将直线y=﹣x ﹣5向上平移5个单位,得到直线_____。
y=3x ﹣2
y= ﹣ x
拓展提升
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
y=2x
y=-2x
y=-3x
y=-x
y=3x
y=x
1、(1)观察正比例函数y = - 3x与y = 3x , y = -2 x 与y = 2x, y = -x与y = x 的位置关于 对称,比例系数K的关系是 ;
(2)当 越大时,图象越靠近
y轴。
X轴 、Y轴
互为相反数
|k|
