2021-2022学年人教版七年级下册5.3平行线的性质课后培优(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级下册5.3平行线的性质课后培优(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 574.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 11:55:53 | ||
图片预览


文档简介
5.3 平行线的性质
一、单选题
1.如图,已知直线,把三角尺的直角顶点放在直线上.若∠1=36°,则∠2的度数为( )
A.116° B.124° C.144° D.126°
2.如图,要使直线l1与l2平行,则需直线l1绕点O至少旋转的度数是( )
A.38° B.42° C.80° D.138°
3.已知:如图,直线a,b被直线c所截,且ab,若∠1=70°,则∠2的度数是( )
A.130° B.80° C.110° D.70°
4.如图,已知∠2=∠B,∠1=35°,则∠D的度数是( )
A.30° B.40° C.50° D.35°
5.如图,直线m⊥直线n,直线b⊥直线n,若∠2=110°,则∠1的度数是( )
A.60° B.65° C.70° D.50°
6.如图,a//b,∠1=80°,∠2=155°,则∠3的度数是( )
A.115° B.110° C.105° D.100°
7.如图,MN∥OF,ON平分∠EOF,∠ONM=35°,∠EMN的度数是( )
A.70° B.60° C.50° D.40°
8.如图,已知AB∥CD∥EF,∠1=60°,∠3=20°,则∠2的度数是( )
A. B. C. D.
9.如图,AB∥CD,∠1=39°,∠C和∠D互余,∠C的度数为( )
A.39° B.41° C.51° D.61°
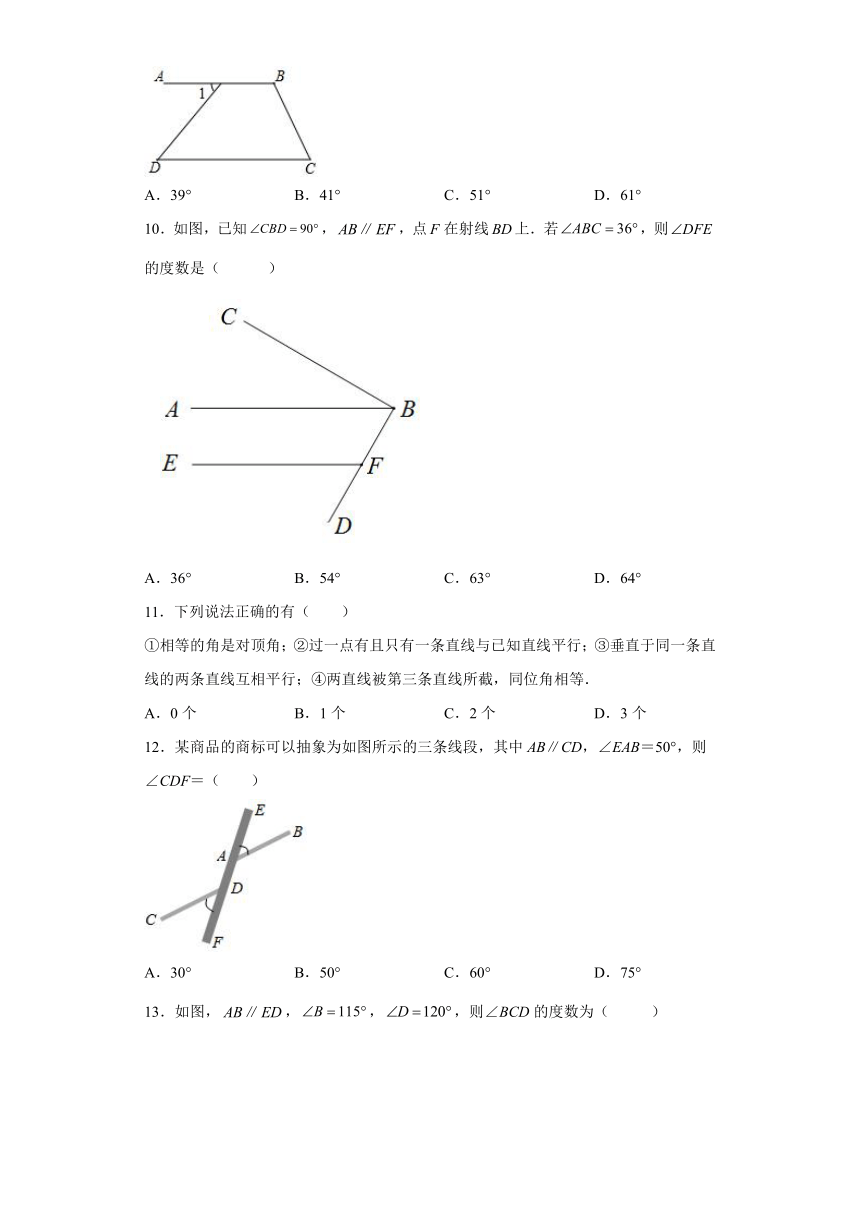
10.如图,已知,,点在射线上.若,则的度数是( )
A.36° B.54° C.63° D.64°
11.下列说法正确的有( )
①相等的角是对顶角;②过一点有且只有一条直线与已知直线平行;③垂直于同一条直线的两条直线互相平行;④两直线被第三条直线所截,同位角相等.
A.0个 B.1个 C.2个 D.3个
12.某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=50°,则∠CDF=( )
A.30° B.50° C.60° D.75°
13.如图,,,,则∠BCD的度数为( )
A.125° B.135° C.115° D.105°
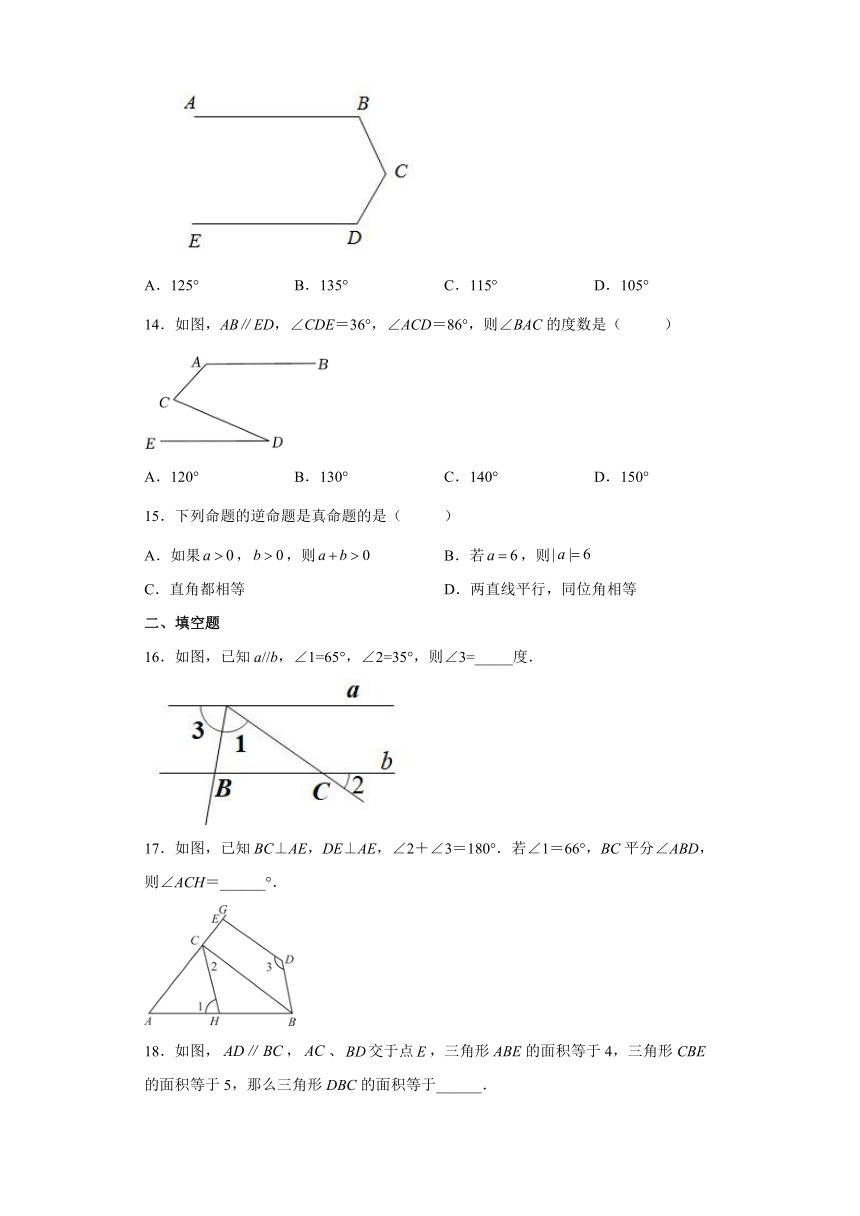
14.如图,AB∥ED,∠CDE=36°,∠ACD=86°,则∠BAC的度数是( )
A.120° B.130° C.140° D.150°
15.下列命题的逆命题是真命题的是( )
A.如果,,则 B.若,则
C.直角都相等 D.两直线平行,同位角相等
二、填空题
16.如图,已知a//b,∠1=65°,∠2=35°,则∠3=_____度.
17.如图,已知BC⊥AE,DE⊥AE,∠2+∠3=180°.若∠1=66°,BC平分∠ABD,则∠ACH=______°.
18.如图,,、交于点,三角形ABE的面积等于4,三角形CBE的面积等于5,那么三角形DBC的面积等于______.
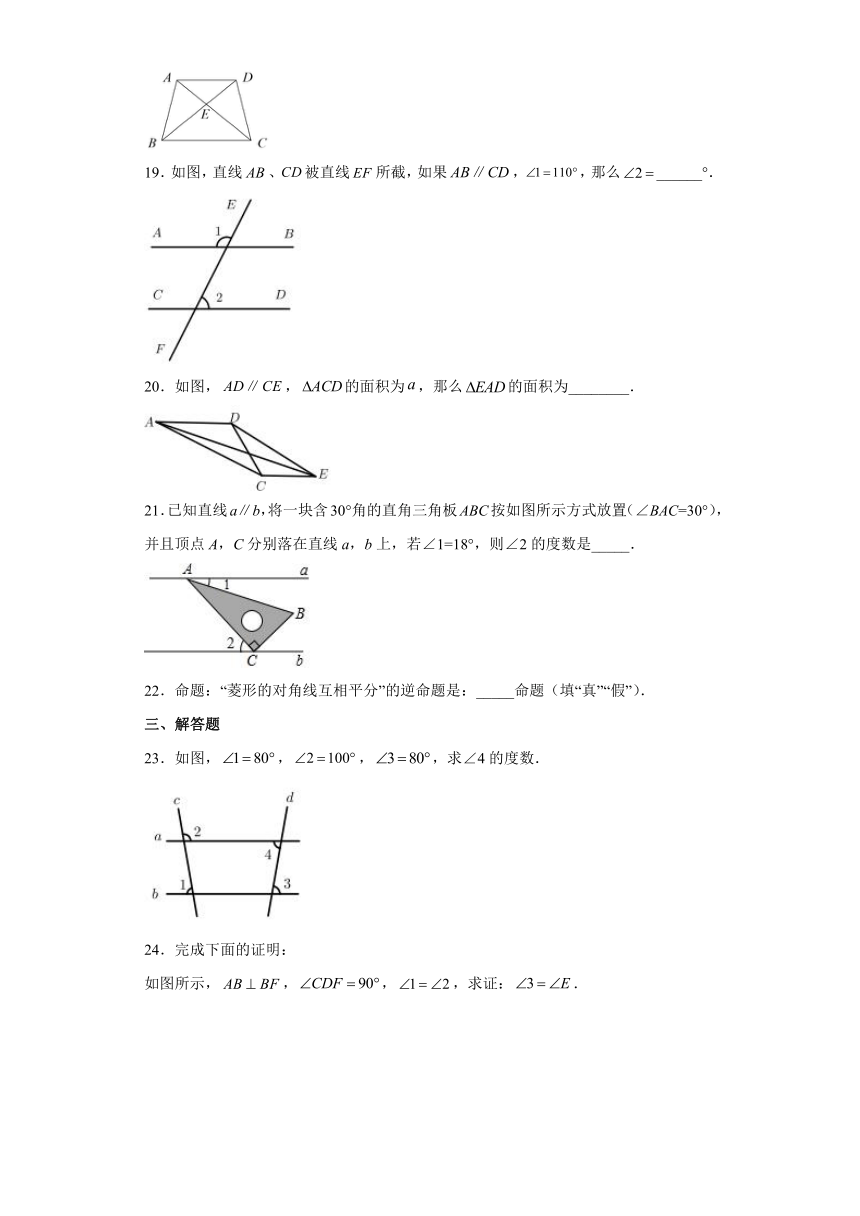
19.如图,直线、被直线所截,如果,,那么______°.
20.如图,,的面积为,那么的面积为________.
21.已知直线a∥b,将一块含30°角的直角三角板ABC按如图所示方式放置(∠BAC=30°),并且顶点A,C分别落在直线a,b上,若∠1=18°,则∠2的度数是_____.
22.命题:“菱形的对角线互相平分”的逆命题是:_____命题(填“真”“假”).
三、解答题
23.如图,,,,求∠4的度数.
24.完成下面的证明:
如图所示,,,,求证:.
证明:
① (②)
(③)
④ (⑤)
⑥ (⑦)
(⑧)
25.如图所示,已知平分,,那么与相等吗?完成下面的填空.
平分(已知)
______(______),
(已知),
______(______),
____________(______),
(______).
26.【问题背景】同学们,我们一起观察小猪的猪蹄,你会发现一个我们熟悉的几何图形,我们就把这个图形形象的称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.
(1)如图①,ABCD,E为AB,CD之间一点,连接BE,DE,得到∠BED.试探究∠BED与∠B、∠D之间的数量关系,并说明理由.
(2)请你利用上述“猪蹄模型”得到的结论或解题方法,完成下面的问题:
①【类比探究】如图②,ABCD,线段AD与线段BC相交于点E,∠BAD=36°,∠BCD=80°,EF平分∠BED交直线AB于点F,则∠BEF=______°.
②【拓展延伸】如图③,ABCD,线段AD与线段BC相交于点E,∠BAD=36°,∠BCD=80°,过点D作DGCB交直线AB于点G,AH平分∠BAD,DH平分∠CDG,则∠AHD=______°.
27.(1)如图,已知,,求证:.
证明:∵,
∴∠______=∠______(两直线平行,______)
又∵,
∴∠______=∠______,
∴____________.(______,两直线平行)
(2)如图,已知,,求证:.
28.如图,已知,,.求证:.
试卷第1页,共3页
参考答案:
1.D
解:∵∠1=36°,
∴∠3=180°-∠1-90°=180°-36°-90°=54°,
∵ab,
∴∠2=180°-∠3=126°.
故选:D.
2.A
解:要使直线l1与l2平行,则,
要使直线l1与l2平行,直线l1绕点O至少旋转
故选:A.
3.C
解:如图,
∵,
∴,
∵,
∴.
故选:B
4.D
解:∵∠2=∠B,
∴AB∥CD,
∴∠1=∠D,
∵∠1=35°,
∴∠D=35°,
故选:D.
5.C
如图:
∵直线m⊥直线n,直线b⊥直线n,
∴m∥b,
∴∠1=∠3,
∵∠2=110°,
∴∠3=180°﹣∠2=70°,
∴∠1=70°,
故选:C.
6.C
解:过作,
,
,
,
,
,
,
故选:C.
7.A
解:,
,
平分,
,
,
,
,
故选:A.
8.D
解:∵ABEF,
∴∠AEF=∠1,
∵∠1=60°,
∴∠AEF=60°,
∵∠3=20°,
∴∠CEF=60°-20°=40°,
∵CDEF,
∴∠2+∠CEF=180°,
∴∠2=180°-40°=140°.
故选D.
9.C
解:∵ABCD,∠1=39°,
∴∠D=∠1=39°,
∵∠C和∠D互余,
∴∠C=90°﹣∠D=51°.
故选:C.
10.B
解:由题意可知:∠ABF=90°-∠ABC=54°,
∵,
∴∠DFE=∠ABF=54°,
故选:B.
11.A
解:①对顶角相等,相等的角不一定是对顶角,故①错误;
②过直线外一点有且只有一条直线与已知直线平行,故②错误;
③在同一个平面内,垂直于同一条直线的两条直线互相平行,故③错误;
④两直线平行,同位角相等,故④错误;
故选:A.
12.B
解:延长BA到G,
∵∠GAF与∠EAB是对顶角,
∴∠EAB=∠GAF=50°,
∵AB∥CD,
∴∠CDF=∠GAF=50°,
故选B.
13.A
解:作CF//AB,
∴∠B+∠1=180°,
∵,
∴CF//DE,
∴∠D+∠2=180°,
∴∠B+∠1+∠D+∠2=360°,
∵,,
∴∠1+∠2=125°,
即∠BCD=125°,
故选A.
14.B
作CF∥ED,如图,
∵CF∥ED,
∴∠CDE=∠FCD=36°,
∴∠ACF=86°﹣36°=50°,
∵AB∥ED,CF∥ED,
∴CF∥AB,
∴∠BAC+∠ACF=180°.
∴∠BAC=130°.
故选:B.
15.D
解:A.逆命题为:如果,则,,反例,,故选项A的逆命题是假命题;
B.逆命题为:若,则,反例也成立,故选项B逆命题是假命题;
C.逆命题为:相等角是直角,∠A=∠B=30°,但不是直角,故选项C的逆命题是假命题;
D.逆命题为:同位角相等,两直线平行,根据平行线判定定理知其是真命题,故选项D的逆命题是真命题.
故选择D.
16.80
解:∵,
∴,
∵,
∴,
∵,
∴,
故答案为:80.
17.57
解:∵BC平分∠ABD,
∴∠HBC=∠DBC=,
∵BC⊥AE,DE⊥AE,
∴BC∥DE,
∴∠3+∠DBC=180°,
∵∠2+∠3=180°,
∴∠DBC=∠2,
∴CH∥BD,
∴∠DBA=∠1=66°,
∴∠DBC=∠2=,
∴∠ACH=∠ACB-∠2=90°-33°=57°.
故答案为:57.
18.9
解:,
,
故答案为:9.
19.70
与是对顶角,
,
,,
.
20.
解:如图,过作,交的延长线与,
,
的高等于的长,
,
,
.
故答案为:.
21.48°/48度
解:∵a∥b,
∴∠2=∠1+∠CAB=18°+30°=48°,
故答案为:48°.
22.假
解:“菱形的对角线互相平分”的逆命题是“对角线互相平分的四边形是菱形”,
“对角线互相平分的四边形是菱形”不一定是菱形,可能是平行四边形、矩形等,
故逆命题是假命题,
故答案为:假.
23.80°
解:∵,
∴,
∴,
∴,
∴.
24.①90°;② 垂直的定义;③同位角相等,两直线平行;④EF;⑤内错角相等,两直线平行 ;⑥EF;⑦平行于同一条直线的两直线平行;⑧两直线平行,同位角相等;
证明:∵AB⊥BF
∴∠B= 90° (垂直的定义)
∵∠CDF=90°
∴∠B=∠CDF
∴AB∥CD( 同位角相等,两直线平行)
∵∠1=∠2
∴AB∥ EF( 内错角相等,两直线平行 )
∴CD∥ EF(平行于同一条直线的两直线平行 )
∴∠3=∠E( 两直线平行,同位角相等)
25.3;角平分线的定义;3;等量代换;内错角相等,两直线平行;两直线平行,同位角相等
平分(已知)
(角平分线的定义),
(已知),
(等量代换),
(内错角相等,两直线平行),
(两直线平行,同位角相等).
26.(1)∠B+∠D=∠BED,理由见解析
(2)①58;②148
解:∠B+∠D=∠BED.理由:
过E作EF//AB,
∵AB//CD,
∴AB//EF//CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠B+∠D=∠BEF+∠DEF=∠BED;
(2)
解:①∵ABCD,
∴∠ADC=∠BAD=36°,
∵∠BCD=80°,
∴∠BED=∠BCD+∠ADC=116°,
∵EF平分∠BED,
∴∠BEF=∠BED=58°.
故答案为:58;
②作HF//AB,
∵ABCD,
∴ABHF//CD,
∴∠CDG=180°-∠BCD=100°,
∵AH平分∠BAD,DH平分∠CDG,
∴∠BAH=∠BAD=18°,∠CDH=CDG=50°,
∵ABHF//CD,
∴∠AHF=∠BAH =18°,∠DHF=180°-∠CDH =130°,
∴∠AHD=AHF+∠DHF=148°,
故答案为:148.
27.(1);内错角相等;;;内错角相等;(2)见解析
(1)证明:∵,
∴(两直线平行,内错角相等),
又∵,
∴,
∴.(内错角相等,两直线平行),
故答案为:2,3,内错角相等;1,2;AC,DE,内错角相等;
(2)证明:∵,
∴,
∵,
∴,
∴.
28.见解析
证明:∵,
又,
∴.
∴.
∴.
又,
∴.
∴.
∴.
答案第1页,共2页
一、单选题
1.如图,已知直线,把三角尺的直角顶点放在直线上.若∠1=36°,则∠2的度数为( )
A.116° B.124° C.144° D.126°
2.如图,要使直线l1与l2平行,则需直线l1绕点O至少旋转的度数是( )
A.38° B.42° C.80° D.138°
3.已知:如图,直线a,b被直线c所截,且ab,若∠1=70°,则∠2的度数是( )
A.130° B.80° C.110° D.70°
4.如图,已知∠2=∠B,∠1=35°,则∠D的度数是( )
A.30° B.40° C.50° D.35°
5.如图,直线m⊥直线n,直线b⊥直线n,若∠2=110°,则∠1的度数是( )
A.60° B.65° C.70° D.50°
6.如图,a//b,∠1=80°,∠2=155°,则∠3的度数是( )
A.115° B.110° C.105° D.100°
7.如图,MN∥OF,ON平分∠EOF,∠ONM=35°,∠EMN的度数是( )
A.70° B.60° C.50° D.40°
8.如图,已知AB∥CD∥EF,∠1=60°,∠3=20°,则∠2的度数是( )
A. B. C. D.
9.如图,AB∥CD,∠1=39°,∠C和∠D互余,∠C的度数为( )
A.39° B.41° C.51° D.61°
10.如图,已知,,点在射线上.若,则的度数是( )
A.36° B.54° C.63° D.64°
11.下列说法正确的有( )
①相等的角是对顶角;②过一点有且只有一条直线与已知直线平行;③垂直于同一条直线的两条直线互相平行;④两直线被第三条直线所截,同位角相等.
A.0个 B.1个 C.2个 D.3个
12.某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=50°,则∠CDF=( )
A.30° B.50° C.60° D.75°
13.如图,,,,则∠BCD的度数为( )
A.125° B.135° C.115° D.105°
14.如图,AB∥ED,∠CDE=36°,∠ACD=86°,则∠BAC的度数是( )
A.120° B.130° C.140° D.150°
15.下列命题的逆命题是真命题的是( )
A.如果,,则 B.若,则
C.直角都相等 D.两直线平行,同位角相等
二、填空题
16.如图,已知a//b,∠1=65°,∠2=35°,则∠3=_____度.
17.如图,已知BC⊥AE,DE⊥AE,∠2+∠3=180°.若∠1=66°,BC平分∠ABD,则∠ACH=______°.
18.如图,,、交于点,三角形ABE的面积等于4,三角形CBE的面积等于5,那么三角形DBC的面积等于______.
19.如图,直线、被直线所截,如果,,那么______°.
20.如图,,的面积为,那么的面积为________.
21.已知直线a∥b,将一块含30°角的直角三角板ABC按如图所示方式放置(∠BAC=30°),并且顶点A,C分别落在直线a,b上,若∠1=18°,则∠2的度数是_____.
22.命题:“菱形的对角线互相平分”的逆命题是:_____命题(填“真”“假”).
三、解答题
23.如图,,,,求∠4的度数.
24.完成下面的证明:
如图所示,,,,求证:.
证明:
① (②)
(③)
④ (⑤)
⑥ (⑦)
(⑧)
25.如图所示,已知平分,,那么与相等吗?完成下面的填空.
平分(已知)
______(______),
(已知),
______(______),
____________(______),
(______).
26.【问题背景】同学们,我们一起观察小猪的猪蹄,你会发现一个我们熟悉的几何图形,我们就把这个图形形象的称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.
(1)如图①,ABCD,E为AB,CD之间一点,连接BE,DE,得到∠BED.试探究∠BED与∠B、∠D之间的数量关系,并说明理由.
(2)请你利用上述“猪蹄模型”得到的结论或解题方法,完成下面的问题:
①【类比探究】如图②,ABCD,线段AD与线段BC相交于点E,∠BAD=36°,∠BCD=80°,EF平分∠BED交直线AB于点F,则∠BEF=______°.
②【拓展延伸】如图③,ABCD,线段AD与线段BC相交于点E,∠BAD=36°,∠BCD=80°,过点D作DGCB交直线AB于点G,AH平分∠BAD,DH平分∠CDG,则∠AHD=______°.
27.(1)如图,已知,,求证:.
证明:∵,
∴∠______=∠______(两直线平行,______)
又∵,
∴∠______=∠______,
∴____________.(______,两直线平行)
(2)如图,已知,,求证:.
28.如图,已知,,.求证:.
试卷第1页,共3页
参考答案:
1.D
解:∵∠1=36°,
∴∠3=180°-∠1-90°=180°-36°-90°=54°,
∵ab,
∴∠2=180°-∠3=126°.
故选:D.
2.A
解:要使直线l1与l2平行,则,
要使直线l1与l2平行,直线l1绕点O至少旋转
故选:A.
3.C
解:如图,
∵,
∴,
∵,
∴.
故选:B
4.D
解:∵∠2=∠B,
∴AB∥CD,
∴∠1=∠D,
∵∠1=35°,
∴∠D=35°,
故选:D.
5.C
如图:
∵直线m⊥直线n,直线b⊥直线n,
∴m∥b,
∴∠1=∠3,
∵∠2=110°,
∴∠3=180°﹣∠2=70°,
∴∠1=70°,
故选:C.
6.C
解:过作,
,
,
,
,
,
,
故选:C.
7.A
解:,
,
平分,
,
,
,
,
故选:A.
8.D
解:∵ABEF,
∴∠AEF=∠1,
∵∠1=60°,
∴∠AEF=60°,
∵∠3=20°,
∴∠CEF=60°-20°=40°,
∵CDEF,
∴∠2+∠CEF=180°,
∴∠2=180°-40°=140°.
故选D.
9.C
解:∵ABCD,∠1=39°,
∴∠D=∠1=39°,
∵∠C和∠D互余,
∴∠C=90°﹣∠D=51°.
故选:C.
10.B
解:由题意可知:∠ABF=90°-∠ABC=54°,
∵,
∴∠DFE=∠ABF=54°,
故选:B.
11.A
解:①对顶角相等,相等的角不一定是对顶角,故①错误;
②过直线外一点有且只有一条直线与已知直线平行,故②错误;
③在同一个平面内,垂直于同一条直线的两条直线互相平行,故③错误;
④两直线平行,同位角相等,故④错误;
故选:A.
12.B
解:延长BA到G,
∵∠GAF与∠EAB是对顶角,
∴∠EAB=∠GAF=50°,
∵AB∥CD,
∴∠CDF=∠GAF=50°,
故选B.
13.A
解:作CF//AB,
∴∠B+∠1=180°,
∵,
∴CF//DE,
∴∠D+∠2=180°,
∴∠B+∠1+∠D+∠2=360°,
∵,,
∴∠1+∠2=125°,
即∠BCD=125°,
故选A.
14.B
作CF∥ED,如图,
∵CF∥ED,
∴∠CDE=∠FCD=36°,
∴∠ACF=86°﹣36°=50°,
∵AB∥ED,CF∥ED,
∴CF∥AB,
∴∠BAC+∠ACF=180°.
∴∠BAC=130°.
故选:B.
15.D
解:A.逆命题为:如果,则,,反例,,故选项A的逆命题是假命题;
B.逆命题为:若,则,反例也成立,故选项B逆命题是假命题;
C.逆命题为:相等角是直角,∠A=∠B=30°,但不是直角,故选项C的逆命题是假命题;
D.逆命题为:同位角相等,两直线平行,根据平行线判定定理知其是真命题,故选项D的逆命题是真命题.
故选择D.
16.80
解:∵,
∴,
∵,
∴,
∵,
∴,
故答案为:80.
17.57
解:∵BC平分∠ABD,
∴∠HBC=∠DBC=,
∵BC⊥AE,DE⊥AE,
∴BC∥DE,
∴∠3+∠DBC=180°,
∵∠2+∠3=180°,
∴∠DBC=∠2,
∴CH∥BD,
∴∠DBA=∠1=66°,
∴∠DBC=∠2=,
∴∠ACH=∠ACB-∠2=90°-33°=57°.
故答案为:57.
18.9
解:,
,
故答案为:9.
19.70
与是对顶角,
,
,,
.
20.
解:如图,过作,交的延长线与,
,
的高等于的长,
,
,
.
故答案为:.
21.48°/48度
解:∵a∥b,
∴∠2=∠1+∠CAB=18°+30°=48°,
故答案为:48°.
22.假
解:“菱形的对角线互相平分”的逆命题是“对角线互相平分的四边形是菱形”,
“对角线互相平分的四边形是菱形”不一定是菱形,可能是平行四边形、矩形等,
故逆命题是假命题,
故答案为:假.
23.80°
解:∵,
∴,
∴,
∴,
∴.
24.①90°;② 垂直的定义;③同位角相等,两直线平行;④EF;⑤内错角相等,两直线平行 ;⑥EF;⑦平行于同一条直线的两直线平行;⑧两直线平行,同位角相等;
证明:∵AB⊥BF
∴∠B= 90° (垂直的定义)
∵∠CDF=90°
∴∠B=∠CDF
∴AB∥CD( 同位角相等,两直线平行)
∵∠1=∠2
∴AB∥ EF( 内错角相等,两直线平行 )
∴CD∥ EF(平行于同一条直线的两直线平行 )
∴∠3=∠E( 两直线平行,同位角相等)
25.3;角平分线的定义;3;等量代换;内错角相等,两直线平行;两直线平行,同位角相等
平分(已知)
(角平分线的定义),
(已知),
(等量代换),
(内错角相等,两直线平行),
(两直线平行,同位角相等).
26.(1)∠B+∠D=∠BED,理由见解析
(2)①58;②148
解:∠B+∠D=∠BED.理由:
过E作EF//AB,
∵AB//CD,
∴AB//EF//CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠B+∠D=∠BEF+∠DEF=∠BED;
(2)
解:①∵ABCD,
∴∠ADC=∠BAD=36°,
∵∠BCD=80°,
∴∠BED=∠BCD+∠ADC=116°,
∵EF平分∠BED,
∴∠BEF=∠BED=58°.
故答案为:58;
②作HF//AB,
∵ABCD,
∴ABHF//CD,
∴∠CDG=180°-∠BCD=100°,
∵AH平分∠BAD,DH平分∠CDG,
∴∠BAH=∠BAD=18°,∠CDH=CDG=50°,
∵ABHF//CD,
∴∠AHF=∠BAH =18°,∠DHF=180°-∠CDH =130°,
∴∠AHD=AHF+∠DHF=148°,
故答案为:148.
27.(1);内错角相等;;;内错角相等;(2)见解析
(1)证明:∵,
∴(两直线平行,内错角相等),
又∵,
∴,
∴.(内错角相等,两直线平行),
故答案为:2,3,内错角相等;1,2;AC,DE,内错角相等;
(2)证明:∵,
∴,
∵,
∴,
∴.
28.见解析
证明:∵,
又,
∴.
∴.
∴.
又,
∴.
∴.
∴.
答案第1页,共2页
