2021-2022学年北师大版数学八年级下册1.2直角三角形课后训练B(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版数学八年级下册1.2直角三角形课后训练B(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 420.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 00:00:00 | ||
图片预览



文档简介
北师大数学八年级下册第一章 三角形的证明 1.2直角三角形 课后训练A(含答案)
姓名:___________班级:___________
一、单选题
1.记的三边分别为a,b,c,则无法判断为直角三角形的是( )
A. B.
C. D.
2.如图,,于点,与交于点,若,则等于( )
A.20° B.50° C.70° D.110°
3.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是平分线,CF交AD于点G,交BE于点H,下列结论①S△ABE=S△BCE;②∠AFG=∠AGF;③BH=CH;④∠FAG=2∠ACF.正确的是( )
A.①②③ B.③④ C.①②④ D.①②③④
4.已知a,b,c是三角形的三边,若满足,则该三角形的形状是( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
5.如图,直线被直线所截,,,则( ).
A.36° B.54° C.46° D.44°
6.将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是( )
A.45° B.50° C.60° D.75°
7.下列命题中正确的是( )
A.如果a,b,c是一组勾股数,那么,,也是一组勾股数
B.如果一个三角形的三个内角的度数之比是1:2:3,那么这个三角形三个内角所对的边之比也是1:2:3
C.如果直角三角形的两边分别是3,4,那么斜边一定是5
D.任何一个定理都有逆定理
8.如图,直线a∥b,直线AB⊥AC,若∠1=52°,则∠2的度数是( )
A.38° B.42° C.48° D.52°
9.如图,在中,,,点是上一点,将沿线段翻折,使得点落在处,若,则( )
A. B. C. D.
10.如图,点为的边上一点,且满足,作于点,若,,则的度数为( )
A.56° B.58° C.60° D.62°
11.如图,△ABC中,AC=8,点D,E分别在BC,AC上,F是BD的中点.若AB=AD,EF=EC,则EF的长是( )
A.3 B.4 C.5 D.6
12.如图,△ABC的角平分线 CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=∠CGE.其中正确的结论是( )
A.只有①③ B.只有②④
C.只有①③④ D.①②③④
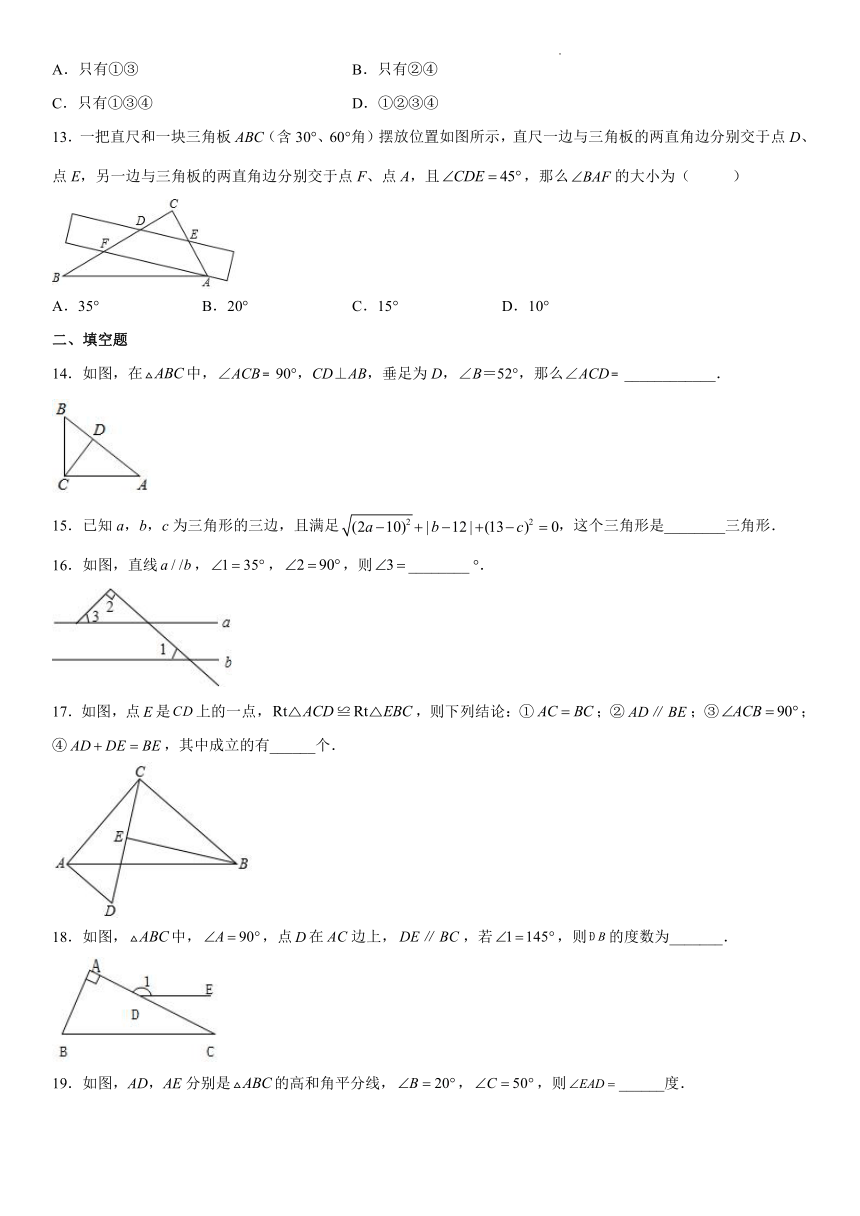
13.一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且,那么的大小为( )
A.35° B.20° C.15° D.10°
二、填空题
14.如图,在中,∠ACB﹦90°,CD⊥AB,垂足为D,∠B=52°,那么∠ACD﹦____________.
15.已知a,b,c为三角形的三边,且满足,这个三角形是________三角形.
16.如图,直线,,,则________ °.
17.如图,点是上的一点,,则下列结论:①;②;③;④,其中成立的有______个.
18.如图,中,,点在边上,,若,则的度数为_______.
19.如图,AD,AE分别是的高和角平分线,,,则______度.
20.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交边BC于点DE,E,F分别是AD,AC上的点,连接CE,EF.若AB=10,BC=6,AC=8,则CE+EF的最小值是________.
三、解答题
21.如图所示,直线AD和BC相交于O,AB∥CD,AD⊥BC于O,∠B=50°,求∠A和∠C.
22.已知中,,,点D为BC边上一点,连接AD,作于点E,于点F.
(1)若AD为的角平分线(如图1),图中、有何数量关系?请说明理由.
(2)若AD为的高(如图2),求图中、的度数.
23.如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
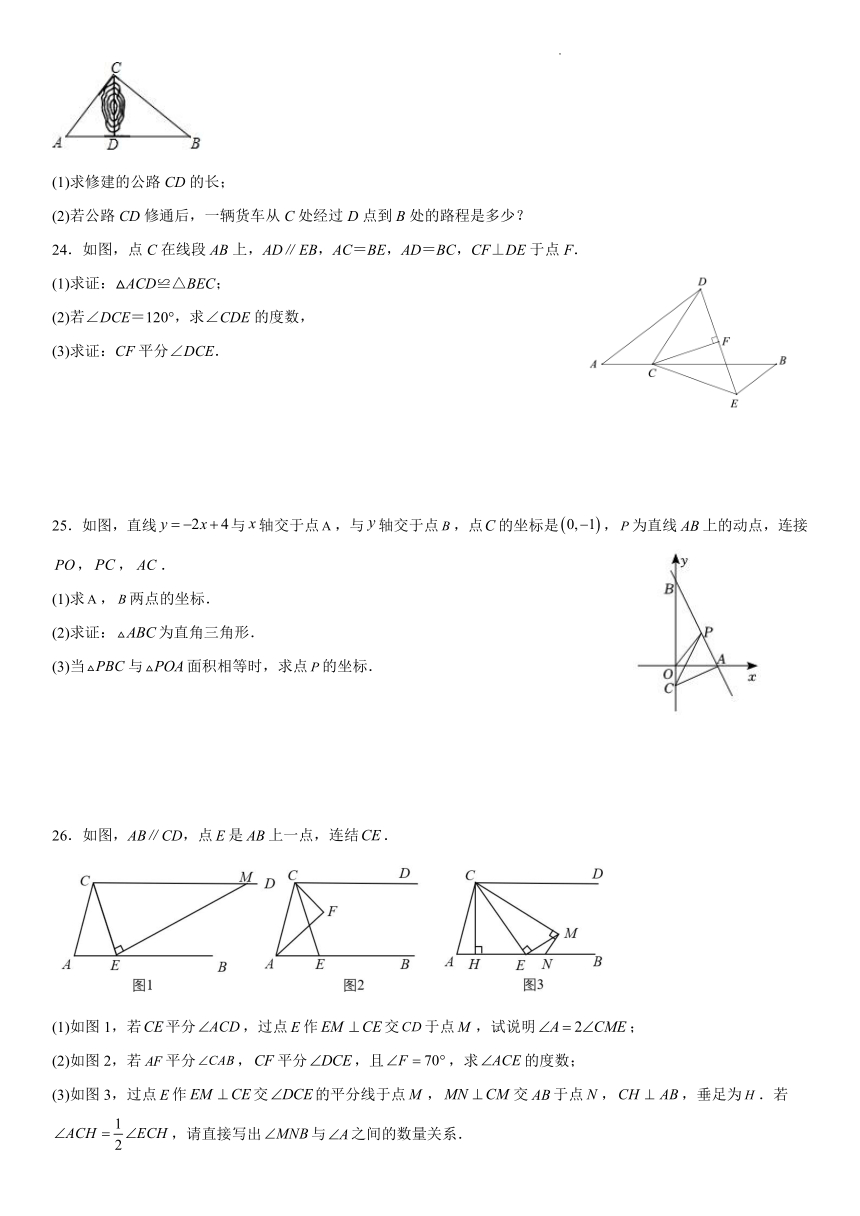
(1)求修建的公路CD的长;
(2)若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?
24.如图,点C在线段AB上,ADEB,AC=BE,AD=BC,CF⊥DE于点F.
(1)求证:△ACD≌△BEC;
(2)若∠DCE=120°,求∠CDE的度数,
(3)求证:CF平分∠DCE.
25.如图,直线与轴交于点,与轴交于点,点的坐标是,为直线上的动点,连接,,.
(1)求,两点的坐标.
(2)求证:为直角三角形.
(3)当与面积相等时,求点的坐标.
26.如图,AB∥CD,点是上一点,连结.
(1)如图1,若平分,过点作交于点,试说明;
(2)如图2,若平分,平分,且,求的度数;
(3)如图3,过点作交的平分线于点,交于点,,垂足为.若,请直接写出与之间的数量关系.
参考答案:
1.A 2.C 3.C 4.A 5.B 6.D 7.A 8.A 9.C 10.B 11.B 12.C13.C
14.
15.直角
16.55
17.1
18.
19.15
20.4.8
21.解:于点,
,
,
,
,
.
22.解:(1)∵AD为的角平分线
∴
又∵,
∴
∴
即
(2)∵AD为的高
∴
又∵
∴
又∵
∴
又∵,
∴,
∴
23.(1)解:∵AC=15km,BC=20km,AB=25km,
152+202=252,
∴△ACB是直角三角形,∠ACB=90°,
∵AC×BC=AB×CD,
∴CD=AC×BC÷AB=12(km).
故修建的公路CD的长是12km;
(2)解:在Rt△BDC中,BD= =16(km),
一辆货车从C处经过D点到B处的路程=CD+BD=12+16=28(km).
故一辆货车从C处经过D点到B处的路程是28km.
24.(1)∵ADBE,
∴∠A=∠B,
在△ACD和△BEC中,
∵,
∴△ACD≌△BEC(SAS),
(2)
如图,
△ACD≌△BEC
,
(3)∵△ACD≌△BEC,
∴CD=CE,
又∵CF⊥DE,
∴CF平分∠DCE.
25.(1)∵直线与轴交于点,与轴交于点,
∴令,则,解得,
∴,
令,则,
∴.
(2)∵,,
∴,
∵在中,,
在中,,
∴,
又∵,
∴,
由勾股定理逆定理知,为直角三角形
(3)设,
∵与面积相等,
则,
∴或,
∴或,
∴或.
26.(1)解:∵AB∥CD,
∴∠A+∠ACD=180°,
∵平分,
∴∠ACD=2∠ECD,
∴∠A+2∠ECD=180°,即∠A=2(90°-∠ECD),
∵,
∴∠CEM=90°,
∴∠CME+∠ECD=90°,即∠CME=90°-∠ECD,
∴;
(2)
解:∵平分,平分,
∴∠BAC=2∠CAF,∠DCE=2∠ECF,
∵,
∴∠CAF+∠ECF+∠ACE=180°-∠F=110°,
∴∠CAF+∠ECF=110°-∠ACE,
∴∠BAC+∠DCE =2(∠CAF+∠ECF)=2(110°-∠ACE),
∵AB∥CD,
∴∠BAC+∠ACD=180°,即∠BAC+∠DCE+∠ACE=180°,
∴2(110°-∠ACE)+∠ACE=180°,
∴∠ACE=40°;
(3)
解:∠MNB+∠A=135°,理由如下:
设 ,
∵CH⊥AB,
∴∠ACH=90°-x,∠ECH+∠CEH=90°,
∵,
∴∠ECH=180°-2x,
∵CE⊥EM,
∴∠MEN+∠CEH=90°,∠MCE+∠CME=90°,
∴∠ECH=∠MEN=180°-2x,
∵AB∥CD,
∴CH⊥CD,
∴∠ECH+∠DCE=90°,
∴∠DCE=2x-90°,
∵CM平分∠DCE,
∴∠ECM=x-45°,
∵CM⊥MN,
∴∠CME+∠EMN=90°,
∴∠EMN=∠ECM= x-45°,
∵∠MNB=∠MEN+∠EMN,
∴∠MNB=180°-2x+ x-45°=135°-x,
即∠MNB+∠A=135°.
答案第1页,共2页
姓名:___________班级:___________
一、单选题
1.记的三边分别为a,b,c,则无法判断为直角三角形的是( )
A. B.
C. D.
2.如图,,于点,与交于点,若,则等于( )
A.20° B.50° C.70° D.110°
3.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是平分线,CF交AD于点G,交BE于点H,下列结论①S△ABE=S△BCE;②∠AFG=∠AGF;③BH=CH;④∠FAG=2∠ACF.正确的是( )
A.①②③ B.③④ C.①②④ D.①②③④
4.已知a,b,c是三角形的三边,若满足,则该三角形的形状是( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
5.如图,直线被直线所截,,,则( ).
A.36° B.54° C.46° D.44°
6.将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是( )
A.45° B.50° C.60° D.75°
7.下列命题中正确的是( )
A.如果a,b,c是一组勾股数,那么,,也是一组勾股数
B.如果一个三角形的三个内角的度数之比是1:2:3,那么这个三角形三个内角所对的边之比也是1:2:3
C.如果直角三角形的两边分别是3,4,那么斜边一定是5
D.任何一个定理都有逆定理
8.如图,直线a∥b,直线AB⊥AC,若∠1=52°,则∠2的度数是( )
A.38° B.42° C.48° D.52°
9.如图,在中,,,点是上一点,将沿线段翻折,使得点落在处,若,则( )
A. B. C. D.
10.如图,点为的边上一点,且满足,作于点,若,,则的度数为( )
A.56° B.58° C.60° D.62°
11.如图,△ABC中,AC=8,点D,E分别在BC,AC上,F是BD的中点.若AB=AD,EF=EC,则EF的长是( )
A.3 B.4 C.5 D.6
12.如图,△ABC的角平分线 CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=∠CGE.其中正确的结论是( )
A.只有①③ B.只有②④
C.只有①③④ D.①②③④
13.一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且,那么的大小为( )
A.35° B.20° C.15° D.10°
二、填空题
14.如图,在中,∠ACB﹦90°,CD⊥AB,垂足为D,∠B=52°,那么∠ACD﹦____________.
15.已知a,b,c为三角形的三边,且满足,这个三角形是________三角形.
16.如图,直线,,,则________ °.
17.如图,点是上的一点,,则下列结论:①;②;③;④,其中成立的有______个.
18.如图,中,,点在边上,,若,则的度数为_______.
19.如图,AD,AE分别是的高和角平分线,,,则______度.
20.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交边BC于点DE,E,F分别是AD,AC上的点,连接CE,EF.若AB=10,BC=6,AC=8,则CE+EF的最小值是________.
三、解答题
21.如图所示,直线AD和BC相交于O,AB∥CD,AD⊥BC于O,∠B=50°,求∠A和∠C.
22.已知中,,,点D为BC边上一点,连接AD,作于点E,于点F.
(1)若AD为的角平分线(如图1),图中、有何数量关系?请说明理由.
(2)若AD为的高(如图2),求图中、的度数.
23.如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB.
(1)求修建的公路CD的长;
(2)若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?
24.如图,点C在线段AB上,ADEB,AC=BE,AD=BC,CF⊥DE于点F.
(1)求证:△ACD≌△BEC;
(2)若∠DCE=120°,求∠CDE的度数,
(3)求证:CF平分∠DCE.
25.如图,直线与轴交于点,与轴交于点,点的坐标是,为直线上的动点,连接,,.
(1)求,两点的坐标.
(2)求证:为直角三角形.
(3)当与面积相等时,求点的坐标.
26.如图,AB∥CD,点是上一点,连结.
(1)如图1,若平分,过点作交于点,试说明;
(2)如图2,若平分,平分,且,求的度数;
(3)如图3,过点作交的平分线于点,交于点,,垂足为.若,请直接写出与之间的数量关系.
参考答案:
1.A 2.C 3.C 4.A 5.B 6.D 7.A 8.A 9.C 10.B 11.B 12.C13.C
14.
15.直角
16.55
17.1
18.
19.15
20.4.8
21.解:于点,
,
,
,
,
.
22.解:(1)∵AD为的角平分线
∴
又∵,
∴
∴
即
(2)∵AD为的高
∴
又∵
∴
又∵
∴
又∵,
∴,
∴
23.(1)解:∵AC=15km,BC=20km,AB=25km,
152+202=252,
∴△ACB是直角三角形,∠ACB=90°,
∵AC×BC=AB×CD,
∴CD=AC×BC÷AB=12(km).
故修建的公路CD的长是12km;
(2)解:在Rt△BDC中,BD= =16(km),
一辆货车从C处经过D点到B处的路程=CD+BD=12+16=28(km).
故一辆货车从C处经过D点到B处的路程是28km.
24.(1)∵ADBE,
∴∠A=∠B,
在△ACD和△BEC中,
∵,
∴△ACD≌△BEC(SAS),
(2)
如图,
△ACD≌△BEC
,
(3)∵△ACD≌△BEC,
∴CD=CE,
又∵CF⊥DE,
∴CF平分∠DCE.
25.(1)∵直线与轴交于点,与轴交于点,
∴令,则,解得,
∴,
令,则,
∴.
(2)∵,,
∴,
∵在中,,
在中,,
∴,
又∵,
∴,
由勾股定理逆定理知,为直角三角形
(3)设,
∵与面积相等,
则,
∴或,
∴或,
∴或.
26.(1)解:∵AB∥CD,
∴∠A+∠ACD=180°,
∵平分,
∴∠ACD=2∠ECD,
∴∠A+2∠ECD=180°,即∠A=2(90°-∠ECD),
∵,
∴∠CEM=90°,
∴∠CME+∠ECD=90°,即∠CME=90°-∠ECD,
∴;
(2)
解:∵平分,平分,
∴∠BAC=2∠CAF,∠DCE=2∠ECF,
∵,
∴∠CAF+∠ECF+∠ACE=180°-∠F=110°,
∴∠CAF+∠ECF=110°-∠ACE,
∴∠BAC+∠DCE =2(∠CAF+∠ECF)=2(110°-∠ACE),
∵AB∥CD,
∴∠BAC+∠ACD=180°,即∠BAC+∠DCE+∠ACE=180°,
∴2(110°-∠ACE)+∠ACE=180°,
∴∠ACE=40°;
(3)
解:∠MNB+∠A=135°,理由如下:
设 ,
∵CH⊥AB,
∴∠ACH=90°-x,∠ECH+∠CEH=90°,
∵,
∴∠ECH=180°-2x,
∵CE⊥EM,
∴∠MEN+∠CEH=90°,∠MCE+∠CME=90°,
∴∠ECH=∠MEN=180°-2x,
∵AB∥CD,
∴CH⊥CD,
∴∠ECH+∠DCE=90°,
∴∠DCE=2x-90°,
∵CM平分∠DCE,
∴∠ECM=x-45°,
∵CM⊥MN,
∴∠CME+∠EMN=90°,
∴∠EMN=∠ECM= x-45°,
∵∠MNB=∠MEN+∠EMN,
∴∠MNB=180°-2x+ x-45°=135°-x,
即∠MNB+∠A=135°.
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
