3.3.3点到直线的距离公式
图片预览





文档简介
课件21张PPT。3.3.3点到直线的距离 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作教学目标 使学生了解点到直线距离公式的推导,能记住点到直线距离的公式,并会应用公式解题。
教学重点:点到直线距离的公式及其应用。
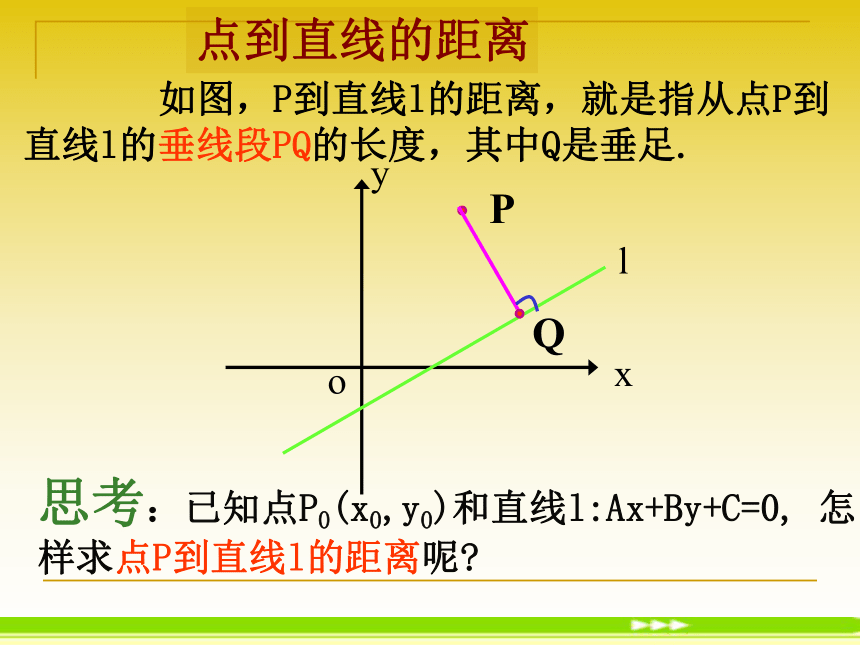
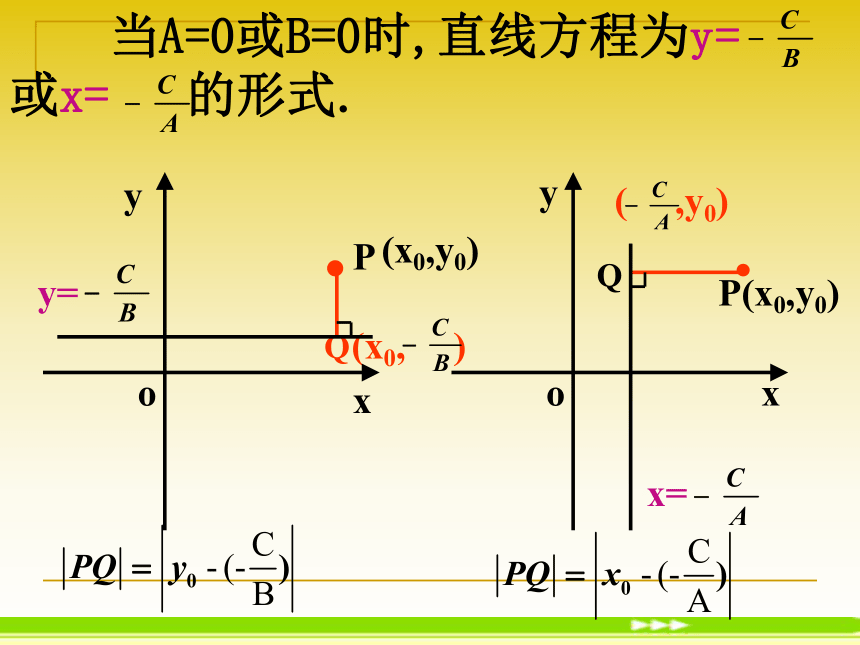
教学难点:点到直线的距离公式的推导。 Q思考:已知点P0(x0,y0)和直线l:Ax+By+C=0, 怎样求点P到直线l的距离呢?点到直线的距离 如图,P到直线l的距离,就是指从点P到直线l的垂线段PQ的长度,其中Q是垂足. 当A=0或B=0时,直线方程为y=或x= 的形式.QQ(x0, )( ,y0)点P(-1,2)到直线3x=2的距离是______.
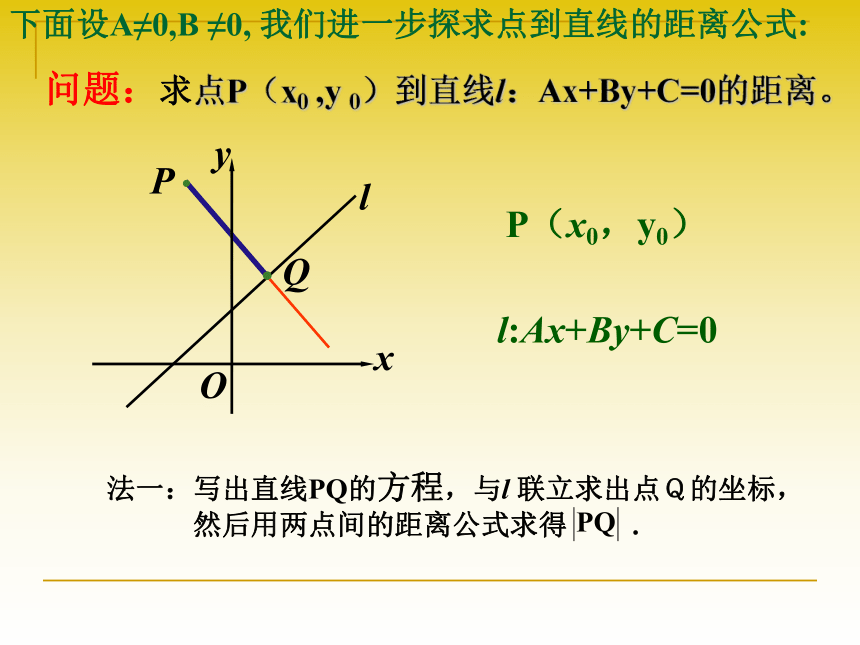
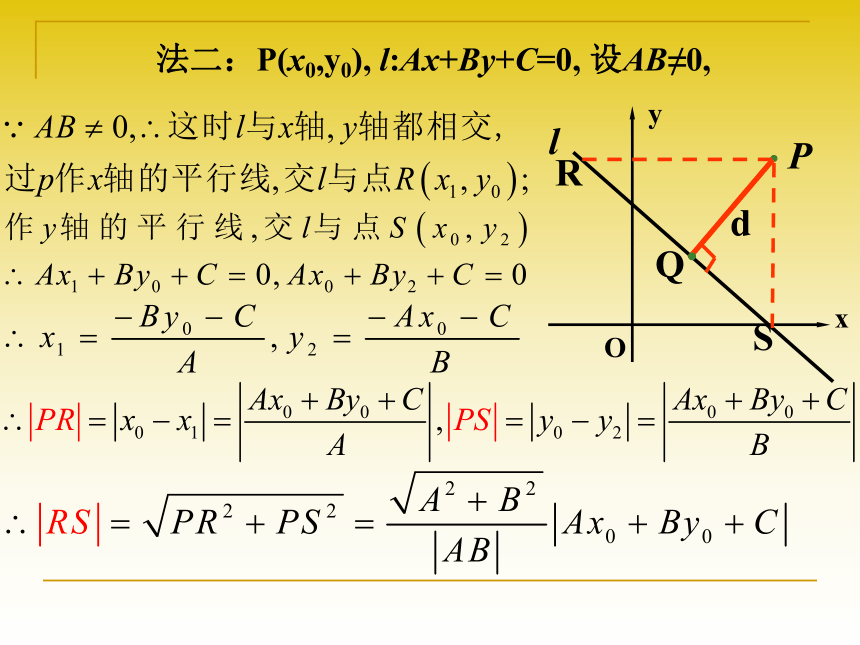
(2)点P(-1,2)到直线3y=2的距离是______.反馈练习一:P(x0,y0)l:Ax+By+C=0问题:求点P(x0 ,y 0)到直线l:Ax+By+C=0的距离。 下面设A≠0,B ≠0, 我们进一步探求点到直线的距离公式:法二:P(x0,y0), l:Ax+By+C=0, 设AB≠0,由三角形面积公式可得:? A=0或B=0,此公式也成立,
但当A=0或B=0时一般不用此
公式计算距离.注: ?在使用该公式前,须将
直线方程化为一般式. 例5:求点P(-1,2)到直线①2x+y-10=0; ②3x=2的距离。解: ①根据点到直线的距离公式,得②如图,直线3x=2平行于y轴,用公式验证,结果怎样?反馈练习二:( )( )DB例6:已知点A(1,3),B(3,1),C(-1,0),求的 面积证明:等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。例题1.证明:建立如图直角坐标系,设P (x,0),x∈( )可求得lAB: lCB: |PE|= |PF|= A到BC的距离h= 因为|PE|+|PF|=h,所以原命题得证。 解:设所求直线的方程为y-2=k(x+1) 即 kx-y+2+k=0 由题意得∴k2+8k+7=0 ∴所求直线的方程为x+y-1=0
或7x+y+5=0.2-1提升习题1、求直线x-4y+6=0和8x+y-18=0与两坐标轴围成的四边形的面积.MNP(提示:M( ,0),N(0, ),直线MN方程:4x+6y-9=0,P(2,2)到直线MN的距离d= ,∴S四边形OMPN = S△OMN+S△PMN= .提升习题2 已知△ABC中,A(1,1),B(m,),C(4,2)(1[分析] 以AC为底,则点B到直线AC的距离就是高,求出S与m之间的函数关系式,求函数最值即可. 点到直线的距离公式的应用
例 3:过点 P(-1,2)引一直线,使它与点 A(2,3),B(4,5)的
距离相等,求该直线的方程. 思维突破:(1)利用代数方法求解,即点到直线的距离公式
建立等式求斜率 k.(2)利用几何性质解题,即 A、B 两点到直线
的距离相等,有两种情况:①直线与 AB 平行;②直线过 AB 的
中点. 已知一点求直线的方程,通常会设点斜式
方程,但要注意斜率不存在的情况.本题解法二利用数形结合
的思想使运算量减少.解法二:当直线与 AB 平行时,k=kAB=1,
∴直线的方程 y-2=1×(x+1),即 x-y+3=0.
当直线过 AB 的中点时,∵AB 的中点为(3,4),课堂总结1.点到直线距离公式
2.特殊情况注意: 化为一般式. xyP0 (x0,y0)O|x1-x0||y1-y0|x0y0y1x1
高中数学老师欧阳文丰制作教学目标 使学生了解点到直线距离公式的推导,能记住点到直线距离的公式,并会应用公式解题。
教学重点:点到直线距离的公式及其应用。
教学难点:点到直线的距离公式的推导。 Q思考:已知点P0(x0,y0)和直线l:Ax+By+C=0, 怎样求点P到直线l的距离呢?点到直线的距离 如图,P到直线l的距离,就是指从点P到直线l的垂线段PQ的长度,其中Q是垂足. 当A=0或B=0时,直线方程为y=或x= 的形式.QQ(x0, )( ,y0)点P(-1,2)到直线3x=2的距离是______.
(2)点P(-1,2)到直线3y=2的距离是______.反馈练习一:P(x0,y0)l:Ax+By+C=0问题:求点P(x0 ,y 0)到直线l:Ax+By+C=0的距离。 下面设A≠0,B ≠0, 我们进一步探求点到直线的距离公式:法二:P(x0,y0), l:Ax+By+C=0, 设AB≠0,由三角形面积公式可得:? A=0或B=0,此公式也成立,
但当A=0或B=0时一般不用此
公式计算距离.注: ?在使用该公式前,须将
直线方程化为一般式. 例5:求点P(-1,2)到直线①2x+y-10=0; ②3x=2的距离。解: ①根据点到直线的距离公式,得②如图,直线3x=2平行于y轴,用公式验证,结果怎样?反馈练习二:( )( )DB例6:已知点A(1,3),B(3,1),C(-1,0),求的 面积证明:等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。例题1.证明:建立如图直角坐标系,设P (x,0),x∈( )可求得lAB: lCB: |PE|= |PF|= A到BC的距离h= 因为|PE|+|PF|=h,所以原命题得证。 解:设所求直线的方程为y-2=k(x+1) 即 kx-y+2+k=0 由题意得∴k2+8k+7=0 ∴所求直线的方程为x+y-1=0
或7x+y+5=0.2-1提升习题1、求直线x-4y+6=0和8x+y-18=0与两坐标轴围成的四边形的面积.MNP(提示:M( ,0),N(0, ),直线MN方程:4x+6y-9=0,P(2,2)到直线MN的距离d= ,∴S四边形OMPN = S△OMN+S△PMN= .提升习题2 已知△ABC中,A(1,1),B(m,),C(4,2)(1
例 3:过点 P(-1,2)引一直线,使它与点 A(2,3),B(4,5)的
距离相等,求该直线的方程. 思维突破:(1)利用代数方法求解,即点到直线的距离公式
建立等式求斜率 k.(2)利用几何性质解题,即 A、B 两点到直线
的距离相等,有两种情况:①直线与 AB 平行;②直线过 AB 的
中点. 已知一点求直线的方程,通常会设点斜式
方程,但要注意斜率不存在的情况.本题解法二利用数形结合
的思想使运算量减少.解法二:当直线与 AB 平行时,k=kAB=1,
∴直线的方程 y-2=1×(x+1),即 x-y+3=0.
当直线过 AB 的中点时,∵AB 的中点为(3,4),课堂总结1.点到直线距离公式
2.特殊情况注意: 化为一般式. xyP0 (x0,y0)O|x1-x0||y1-y0|x0y0y1x1
