北师大版八年级数学下册 2.6 一元一次不等式组 课件 (共17张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 2.6 一元一次不等式组 课件 (共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 743.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 15:44:44 | ||
图片预览





文档简介
(共17张PPT)
2.6 一元一次不等式组(一)
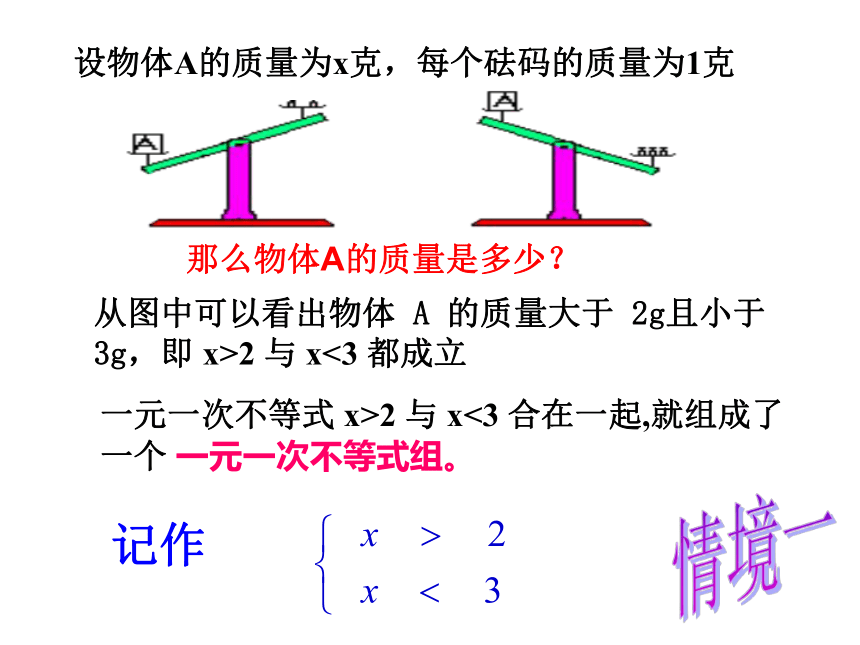
设物体A的质量为x克,每个砝码的质量为1克
从图中可以看出物体 A 的质量大于 2g且小于 3g,即 x>2 与 x<3 都成立
那么物体A的质量是多少?
一元一次不等式 x>2 与 x<3 合在一起,就组成了一个 一元一次不等式组。
记作
某校今年冬季烧煤取暖时间为4个月。如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨。
(1)该校计划每月烧煤多少吨
设该校计划每月烧煤x吨,根据题意,得
4(x+5)>100, ①
且 4(x-5)<68. ②
未知数x同时满足① ②两个条件,把① ②两个不等式
合在一起,就组成一个一元一次不等式组。
记作:
100
)
5
(
4
>
+
x
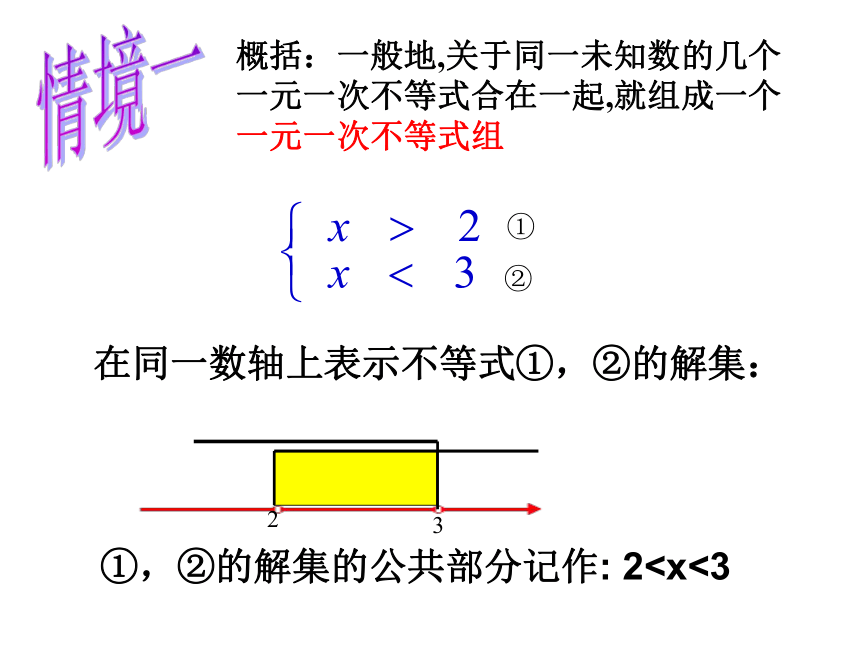
在同一数轴上表示不等式①,②的解集:
2
3
①,②的解集的公共部分记作: 2①
②
概括:一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集。
求不等式组解集的过程,叫做解不等式组。
如 2①
②
的解集
真真假假
成果检验一.
怎么解这个一元一次不等式组,从而得到x的取知范围呢
100
)
5
(
4
>
+
x
解:解不等式(1)得:
x> 20
解不等式(2)得:
x<22
将两个解集表示在同一个数轴上:
此不等式组的解集为:
20解一元一次不等
式组的解题步骤
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的公共部分;
(3)表示出这个不等式组的解集.
解:解不等式①,得
解不等式②,得
例 解不等式组
①
②
因此,原不等式组的解集为:
1<
在同一数轴上表示不等式①,②的解集:
-1
0
1
2
3
4
5
6
7
成果检验二 解下列不等式组
①
②
( 此不等式组无解 )
请同学们猜测下列不等式组的解集,并用数轴验证。
X>5 ②
x≥3 ①
⑴
⑶
⑵
x≤3 ①
X<5 ②
x≤3 ①
X>5 ②
⑷
x≥3 ①
X<5 ②
x≥3 ①
⑴
X>5 ②
⑵
x≤3 ①
X<5 ②
⑶
X>5 ②
x≤3 ①
2
3
0
1
4
5
2
3
0
1
4
5
2
3
0
1
4
5
x>5
x≤3
无解
⑷
x≥3 ①
x<5 ②
2
3
0
1
4
5
3≤x<5
由两个一元一次不等式组成的不等式组的解集,解法如下:
最简不等式组
(a>b) 不等式组的解集 口诀
x>a
x<b
b<x<a
无解
同大取大
同小取小
大小小大中间找
大大小小找不到
选择下列不等式组的解集
①
x ≥ -1
x≥ 2
x≥ 2
x ≥ -1
-1≤ x≤ 2
无解
A
C
D
B
②
x< -1
x< 2
x< 2
x< -1
-1< x< 2
无解
B
D
C
A
A
无解
③
x ≥ -1
x ≥ -1
x< 2
x< 2
-1≤ x< 2
B
D
A
C
C
无解
x< -1
x< -1
④
x≥ 2
x≥ 2
-1< x≥ 2
C
B
A
D
D
B
拓展探究:
解不等式组:
解:解不等式①得,x>-3
解不等式②得,x>5
解不等式③得,x<8
在数轴上表示出①②③的解集
①②③
因此,原不等式组的解集为5<x<8
巩固与思考:
D
A
A. ≥2
D. =2
B. ≤2
C. 无解
1、不等式组 的解集是( )
≥2,
≤2
2、不等式组 的整数解是( )
≤ 1
D. ≤1
A. 1
B. 0
C. 0 , 1
课堂小结
2.一元一次不等式组中各个不等式的解集的公共部分,
叫做这个一元一次不等式组的解集.
4.解一元一次不等式组的步骤:
①求出这个不等式组中各个不等式的解集.
②利用数轴求出这些不等式解集的公共部分.
③表示这个不等式组的解集.
1.一般地,关于同一个未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
3.求不等式组解集的过程,叫做解不等式组.
5.由两个一元一次不等式组成的不等式组的解集
分享你的思考,
是我最大的快乐!
2.6 一元一次不等式组(一)
设物体A的质量为x克,每个砝码的质量为1克
从图中可以看出物体 A 的质量大于 2g且小于 3g,即 x>2 与 x<3 都成立
那么物体A的质量是多少?
一元一次不等式 x>2 与 x<3 合在一起,就组成了一个 一元一次不等式组。
记作
某校今年冬季烧煤取暖时间为4个月。如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨。
(1)该校计划每月烧煤多少吨
设该校计划每月烧煤x吨,根据题意,得
4(x+5)>100, ①
且 4(x-5)<68. ②
未知数x同时满足① ②两个条件,把① ②两个不等式
合在一起,就组成一个一元一次不等式组。
记作:
100
)
5
(
4
>
+
x
在同一数轴上表示不等式①,②的解集:
2
3
①,②的解集的公共部分记作: 2
②
概括:一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集。
求不等式组解集的过程,叫做解不等式组。
如 2
②
的解集
真真假假
成果检验一.
怎么解这个一元一次不等式组,从而得到x的取知范围呢
100
)
5
(
4
>
+
x
解:解不等式(1)得:
x> 20
解不等式(2)得:
x<22
将两个解集表示在同一个数轴上:
此不等式组的解集为:
20
式组的解题步骤
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的公共部分;
(3)表示出这个不等式组的解集.
解:解不等式①,得
解不等式②,得
例 解不等式组
①
②
因此,原不等式组的解集为:
1<
在同一数轴上表示不等式①,②的解集:
-1
0
1
2
3
4
5
6
7
成果检验二 解下列不等式组
①
②
( 此不等式组无解 )
请同学们猜测下列不等式组的解集,并用数轴验证。
X>5 ②
x≥3 ①
⑴
⑶
⑵
x≤3 ①
X<5 ②
x≤3 ①
X>5 ②
⑷
x≥3 ①
X<5 ②
x≥3 ①
⑴
X>5 ②
⑵
x≤3 ①
X<5 ②
⑶
X>5 ②
x≤3 ①
2
3
0
1
4
5
2
3
0
1
4
5
2
3
0
1
4
5
x>5
x≤3
无解
⑷
x≥3 ①
x<5 ②
2
3
0
1
4
5
3≤x<5
由两个一元一次不等式组成的不等式组的解集,解法如下:
最简不等式组
(a>b) 不等式组的解集 口诀
x>a
x<b
b<x<a
无解
同大取大
同小取小
大小小大中间找
大大小小找不到
选择下列不等式组的解集
①
x ≥ -1
x≥ 2
x≥ 2
x ≥ -1
-1≤ x≤ 2
无解
A
C
D
B
②
x< -1
x< 2
x< 2
x< -1
-1< x< 2
无解
B
D
C
A
A
无解
③
x ≥ -1
x ≥ -1
x< 2
x< 2
-1≤ x< 2
B
D
A
C
C
无解
x< -1
x< -1
④
x≥ 2
x≥ 2
-1< x≥ 2
C
B
A
D
D
B
拓展探究:
解不等式组:
解:解不等式①得,x>-3
解不等式②得,x>5
解不等式③得,x<8
在数轴上表示出①②③的解集
①②③
因此,原不等式组的解集为5<x<8
巩固与思考:
D
A
A. ≥2
D. =2
B. ≤2
C. 无解
1、不等式组 的解集是( )
≥2,
≤2
2、不等式组 的整数解是( )
≤ 1
D. ≤1
A. 1
B. 0
C. 0 , 1
课堂小结
2.一元一次不等式组中各个不等式的解集的公共部分,
叫做这个一元一次不等式组的解集.
4.解一元一次不等式组的步骤:
①求出这个不等式组中各个不等式的解集.
②利用数轴求出这些不等式解集的公共部分.
③表示这个不等式组的解集.
1.一般地,关于同一个未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
3.求不等式组解集的过程,叫做解不等式组.
5.由两个一元一次不等式组成的不等式组的解集
分享你的思考,
是我最大的快乐!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
