4.3.3余角和补角

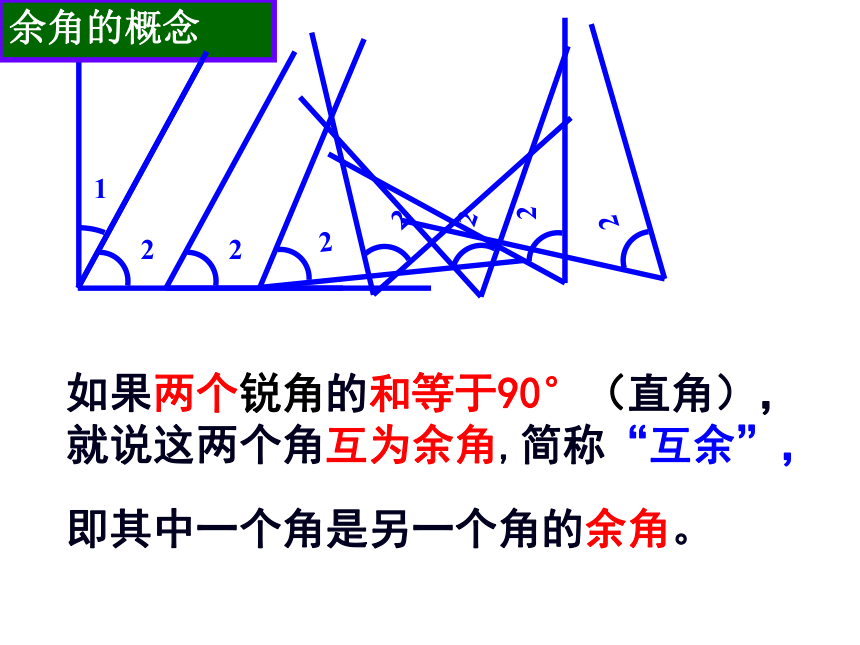
课件19张PPT。海塘大坝要修复加固，施工前要求先测出大坝的倾斜角（即图中的∠1），坝底是石块堆积而成,量角器无法伸入大坝底部测量,聪明的你有什么简单的方法？想一想4.3.3 余角和补角新河镇中学 冯巧红如果两个锐角的和等于90°（直角），就说这两个角互为余角,简称“互余”，余角的概念1即其中一个角是另一个角的余角。如果两个角的和等于180°(平角)，
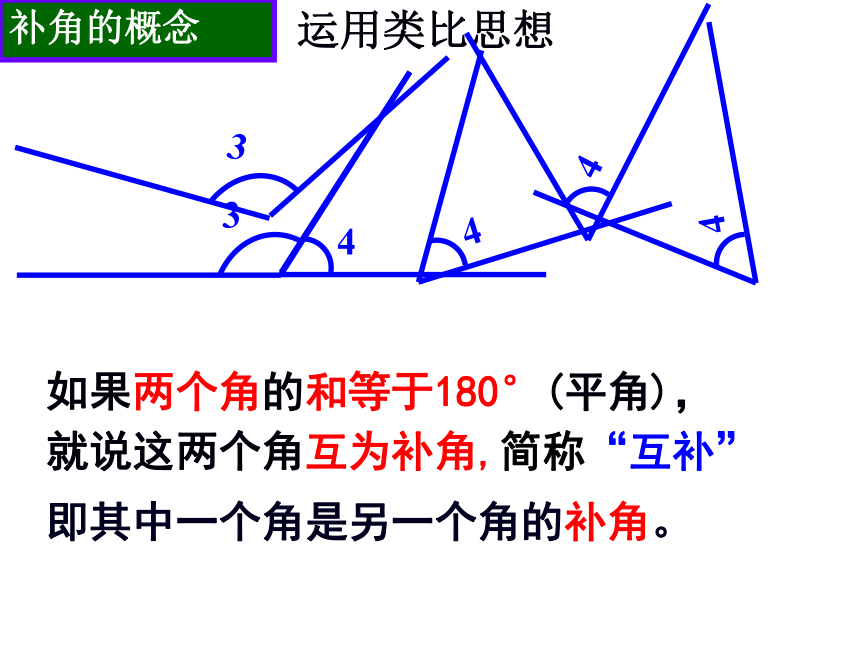
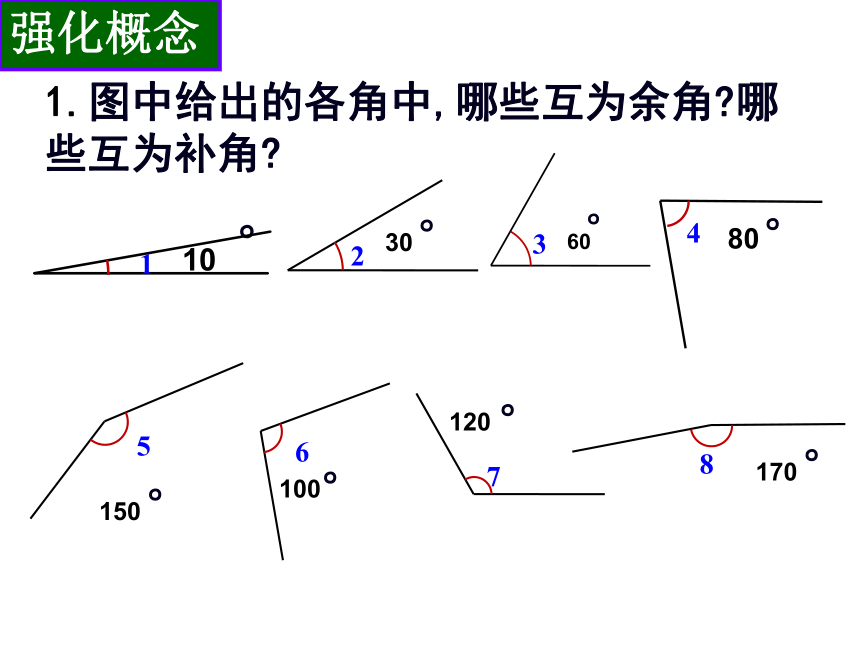
就说这两个角互为补角,简称“互补”运用类比思想补角的概念即其中一个角是另一个角的补角。1.图中给出的各角中,哪些互为余角?哪些互为补角?°强化概念12.填表：强化概念58°148°45°135°90°–x
（ 0 ° ＜X＜90 °）180°–x
（ 0 ° ＜X＜180 °）3.一个角的补角是这个角的余角的3倍，求这个角的度数。强化概念解：设这个角为x °,则它的余角为 ，它的补角为根据题意得：180-x=3（90-x)x=45 °答：这个角为45 °用方程解决几何问题是常用的一种策略。（90-x） °（180-x） ° 测量大坝的倾斜角（即图中的∠1），你有什么简单的方法呢？2方法一：测量∠ 1的补角∠2方法二：测量∠1的余角∠33活学活用2（(2) 图中∠α的余角∠1，∠2的大小有什么关系？ 为什么？(3) 由（2）可得出什么结论？1（1）动手画一画： 已知∠α(如图)，请利用三角板, 画出它的余角。α （解: ∵∠1 +∠α＝90°，
∠2 +∠α ＝90°∴∠1＝∠2同角的余角相等）余角性质图中∠α与∠1互余，∠β与∠2互余，且∠α ＝ ∠β，∠1与∠2的大小有什么关系？为什么？∵ ∠α＋∠1=90°又∵∠α=∠β∴∠1=∠2余角性质∠β＋∠2=90°等角 的余角相等同角（ ）同角或等角的补角是否也相等？又∵∠α=∠β∴∠1=∠2∵∠1 +∠α ＝180°
∠2 +∠β ＝180°(类比)补角性质同角 的补角相等（等角）∵∠1 +∠α ＝180°
∠2 + ∠α ＝180°∴∠1=∠2应用举例1.如图,将一副三角尺按不同位置摆放，∠α与∠β什么关系？）同角的余角相等等角的补角相等（（（（（（（（互余相等相等互补 应用举例2.如图，长方形纸片ABCD，除了图中的四个直角外，你能再折出一个直角吗？ADCBABCD （）4（21）3EOFB′3.如图, 点O为直线AB上一点,射线OE和射线OF分别平分∠AOB′和 ∠BOB′，图中哪些角互为余角？ 2.如图，长方形纸片ABCD，除了图中的四个直角外，你能再折出一个直角吗？应用举例）∠2与∠3∠2与∠4∠1与∠4∠1与∠3AB （）4（21）3EOFB′3.如图, 点O为直线AB上一点,射线OE和射线OF分别平分∠AOB′和 ∠BOB′，图中哪些角互为余角？ B′4.如图, 点O为直线AB上一点, ∠AOB′=∠EOF=90°,若∠1= 2∠4，求：∠2的度数。应用举例(）3∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等同角或等角的补角相等 理一理 . 今天学习的知识小结数学思想方法：类比思想，方程思想折一折，算一算1.如图1，把长方形的一角折叠得到折痕EF，若∠EFB=32 °，求: ∠EFC的度数。（EDCBA如图1FDA（BEC（G如图22、如图2所示折叠，若∠EFG=75 °， 求: ∠BFE的度数
拓展提高 5.如图, 点O为直线AB上一点, OC、OD是一条射线， AOBC1 () 2D找出图中：①相等的角，②互补的角。若∠1= ∠2，解: 相等的角有: ∠AOC= ∠BOD互补的角有:∠1与∠BOD∠2与∠AOC∠1与∠AOC∠2与∠ BOD应用举例做一做3 、已知一个角的补角是它的2.5倍，求这个角的余角。2 、若∠1的补角是∠1的3倍，求∠1的度数。1、已知∠α的余角是∠α的2倍，求 ∠α的度数。 应用举例