19.3 课题学习 选择方案 课件(共30张PPT)
文档属性
| 名称 | 19.3 课题学习 选择方案 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 20:26:18 | ||
图片预览





文档简介
(共30张PPT)
2022年春人教版数学
八年级下册数学精品课件
19.3 课题学习 选择方案
第十九章 一次函数
情境引入
1.会用一次函数知识解决方案选择问题,体会函数
模型思想;(重点、难点)
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方法.
学习目标
20
0
40
60
80
100
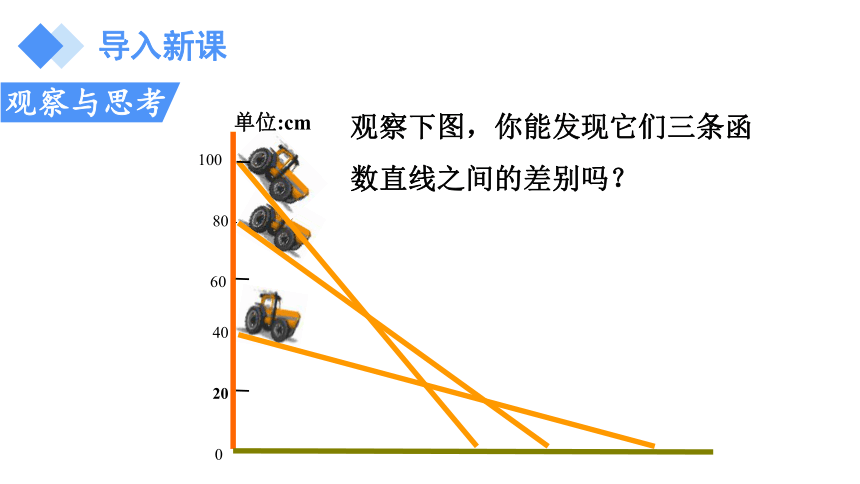
单位:cm
观察下图,你能发现它们三条函数直线之间的差别吗?
导入新课
观察与思考
选择方案
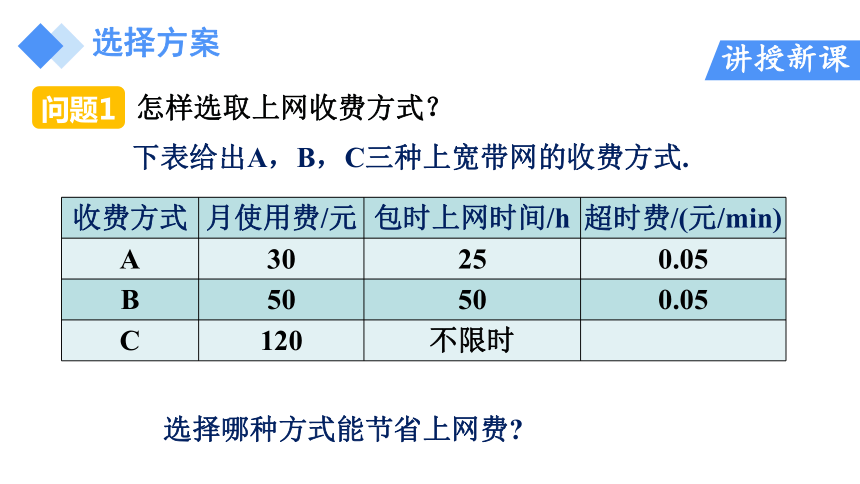
怎样选取上网收费方式?
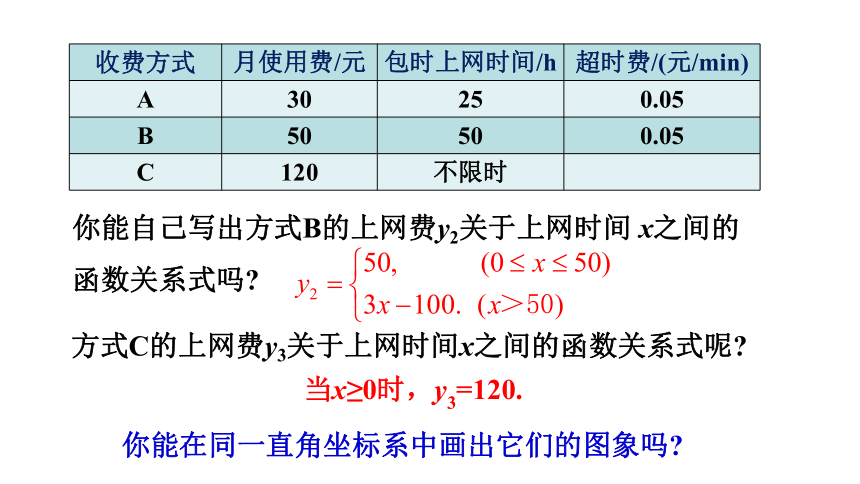
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
选择哪种方式能节省上网费
下表给出A,B,C三种上宽带网的收费方式.
讲授新课
问题1
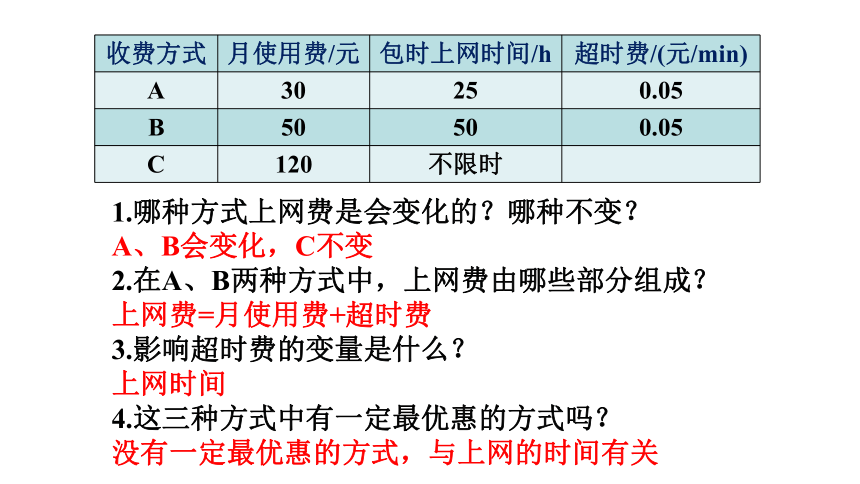
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
设月上网时间为x,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在 x > 0 时,考虑何时
(1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
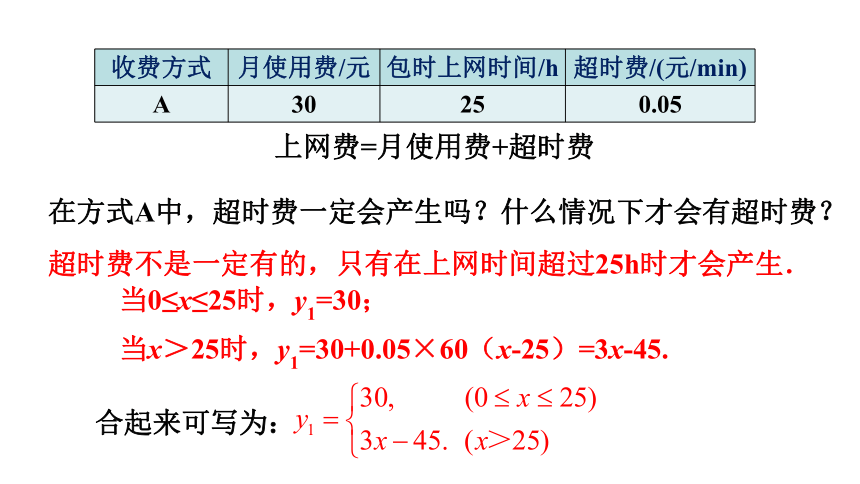
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
超时费不是一定有的,只有在上网时间超过25h时才会产生.
上网费=月使用费+超时费
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗
方式C的上网费y3关于上网时间x之间的函数关系式呢
你能在同一直角坐标系中画出它们的图象吗
当x≥0时,y3=120.
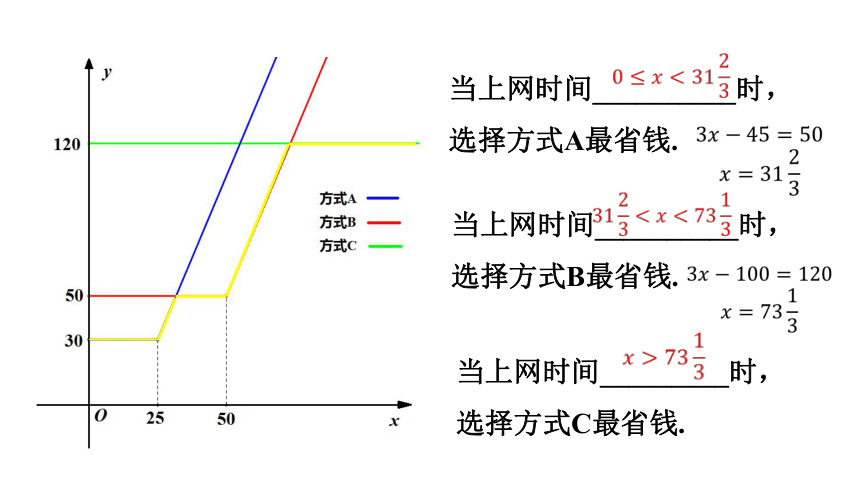
当上网时间__________时,
选择方式A最省钱.
当上网时间__________时,
选择方式B最省钱.
当上网时间_________时,
选择方式C最省钱.
某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费15元,另收通话费
为0.2元/min;
B方案: 零月租费,通话费为0.3元/min.
(1)试写出A,B两种方案所付话费y(元)与通话
时间t(min)之间的函数关系式;
(2)在同一坐标系画出这两个函数的图象,并指出那
种付费方式合算?
做一做
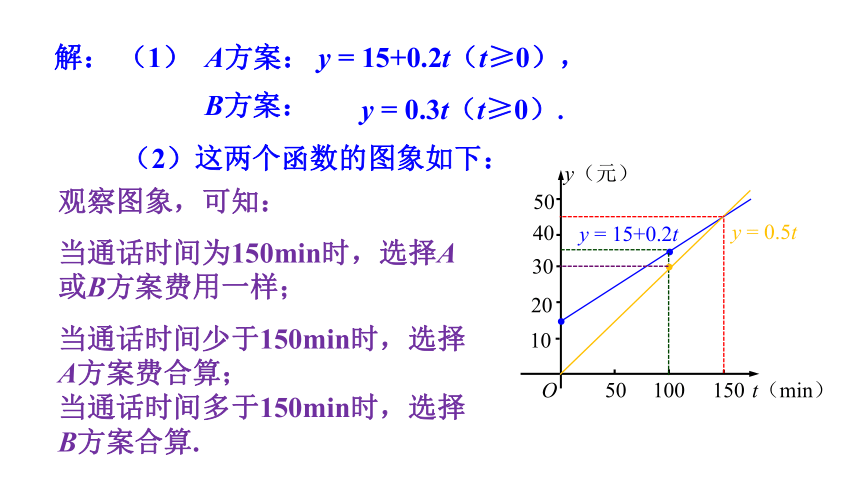
解: (1) A方案: y = 15+0.2t(t≥0),
B方案:
y = 0.3t(t≥0).
(2)这两个函数的图象如下:
t(min)
O
50
150
100
10
20
y(元)
50
30
40
●
●
y = 15+0.2t
y = 0.5t
●
观察图象,可知:
当通话时间为150min时,选择A或B方案费用一样;
当通话时间少于150min时,选择A方案费合算;
当通话时间多于150min时,选择B方案合算.
怎样租车?
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.
现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题2
问题1:租车的方案有哪几种?
共三种:(1)单独租甲种车;(2)单独租乙种车;
(3)甲种车和乙种车都租.
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.
现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题2:如果单独租甲种车需要多少辆?乙种车呢?
问题3:如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于6辆,不能超过8辆.
单独租甲种车要6辆,单独租乙种车要8辆.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题4:要使6名教师至少在每辆车上有一名,你能确定
排除哪种方案?你能确定租车的辆数吗?
说明了车辆总数不会超过6辆,可以排除方案(2)——单独租乙种车;所以租车的辆数只能为6辆.
问题5:在问题3中,合租甲、乙两种车的时候,又有
很多种情况,面对这样的问题,我们怎样处理呢?
方法1:分类讨论——分5种情况;
方法2:设租甲种车x辆,确定x的范围.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
(1)为使240名师生有车坐,
可以确定x的一个范围吗?
(2)为使租车费用不超过2300元,又可以确定x的范围吗?
结合问题的实际意义,你能有几种不同的租车方案 为节省费用应选择其中的哪种方案?
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
x 辆
(6-x)辆
设租用 x 辆甲种客车,则租车费用y(单位:元)是 x 的函数,即
怎样确定 x 的取值范围呢
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
x 辆
(6-x)辆
除了分别计算两种方案的租金外,还有其他选择方案的方法吗?
由函数可知 y 随 x 增大而增大,所以 x = 4时 y 最小.
某校校长暑假将带领该校市级“三好生”去北京旅游.甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内,全部按全票价的6折(即按全票价的60%收费)优惠.”若全票价为240元.
(1)设学生数为 x,甲旅行社收费为 y甲,乙旅行社收费为 y乙,分别计算两家旅行社的收费(写出函数解析式);
做一做
当x < 4时,甲旅行社优惠;当x > 4时,乙旅行社优惠.
(2)当学生数是多少时,两家旅行社的收费一样?
(3)就学生数讨论哪家旅行社更优惠.
当x = 4时,两家旅行社的收费一样.
1.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.
>1500
当堂练习
2. 某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少?
解法一:设该单位参加旅游人数为x.那么选甲旅行社,应付费用80x 元;选乙旅行社,应付(60x+1000)元.记 y1= 80x,y2= 60x+1000.在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
观察图象,可知:当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49人时,选择甲旅行社费用较少;
当人数为51~100人时,选择乙旅行社费用较少.
x/人
50
60
y/元
800
1600
3200
2400
4000
4800
5600
O
10
20
30
40
70
80
90
y1= 80x
y2= 60x+1000
解法二:
(1)当y1=y2,即80x= 60x+1000时,x=50.
所以当人数为50时,选择甲或乙旅行社费用都一样;
(2)当y1 > y2,即80x > 60x+1000时, 得x > 50.
所以当人数为51~100人时 ,选择乙旅行社费用较少;
(3)当y1 < y2,即80x < 60x+1000时,得x<50.
所以当人数为0~49人时,选择甲旅行社费用较少;
解法三:设选择甲、乙旅行社费用之差为y,
则y=y1-y2=80x-(60x+1000)=20x-1000.
画出一次函数y= 20x-1000的图象如下图.
O
20
40
60
-200
-400
-600
-800
-1000
y
x
y= 20x-1000
它与x轴交点为(50,0) 由图可知:
(1)当x=50时,y=0,即y1=y2;
(2)当x>50时,y > 0,即y1 > y2;
(3)当x<50时,y <0,即y1 < y2.
课堂小结
实际问题
函数问题
设变量
找对应关系
函数问题的解
实际问题的解
解释实际意义
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
八年级下册数学精品课件
19.3 课题学习 选择方案
第十九章 一次函数
情境引入
1.会用一次函数知识解决方案选择问题,体会函数
模型思想;(重点、难点)
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方法.
学习目标
20
0
40
60
80
100
单位:cm
观察下图,你能发现它们三条函数直线之间的差别吗?
导入新课
观察与思考
选择方案
怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
选择哪种方式能节省上网费
下表给出A,B,C三种上宽带网的收费方式.
讲授新课
问题1
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
设月上网时间为x,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在 x > 0 时,考虑何时
(1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
超时费不是一定有的,只有在上网时间超过25h时才会产生.
上网费=月使用费+超时费
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗
方式C的上网费y3关于上网时间x之间的函数关系式呢
你能在同一直角坐标系中画出它们的图象吗
当x≥0时,y3=120.
当上网时间__________时,
选择方式A最省钱.
当上网时间__________时,
选择方式B最省钱.
当上网时间_________时,
选择方式C最省钱.
某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费15元,另收通话费
为0.2元/min;
B方案: 零月租费,通话费为0.3元/min.
(1)试写出A,B两种方案所付话费y(元)与通话
时间t(min)之间的函数关系式;
(2)在同一坐标系画出这两个函数的图象,并指出那
种付费方式合算?
做一做
解: (1) A方案: y = 15+0.2t(t≥0),
B方案:
y = 0.3t(t≥0).
(2)这两个函数的图象如下:
t(min)
O
50
150
100
10
20
y(元)
50
30
40
●
●
y = 15+0.2t
y = 0.5t
●
观察图象,可知:
当通话时间为150min时,选择A或B方案费用一样;
当通话时间少于150min时,选择A方案费合算;
当通话时间多于150min时,选择B方案合算.
怎样租车?
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.
现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题2
问题1:租车的方案有哪几种?
共三种:(1)单独租甲种车;(2)单独租乙种车;
(3)甲种车和乙种车都租.
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.
现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题2:如果单独租甲种车需要多少辆?乙种车呢?
问题3:如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于6辆,不能超过8辆.
单独租甲种车要6辆,单独租乙种车要8辆.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题4:要使6名教师至少在每辆车上有一名,你能确定
排除哪种方案?你能确定租车的辆数吗?
说明了车辆总数不会超过6辆,可以排除方案(2)——单独租乙种车;所以租车的辆数只能为6辆.
问题5:在问题3中,合租甲、乙两种车的时候,又有
很多种情况,面对这样的问题,我们怎样处理呢?
方法1:分类讨论——分5种情况;
方法2:设租甲种车x辆,确定x的范围.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
(1)为使240名师生有车坐,
可以确定x的一个范围吗?
(2)为使租车费用不超过2300元,又可以确定x的范围吗?
结合问题的实际意义,你能有几种不同的租车方案 为节省费用应选择其中的哪种方案?
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
x 辆
(6-x)辆
设租用 x 辆甲种客车,则租车费用y(单位:元)是 x 的函数,即
怎样确定 x 的取值范围呢
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
x 辆
(6-x)辆
除了分别计算两种方案的租金外,还有其他选择方案的方法吗?
由函数可知 y 随 x 增大而增大,所以 x = 4时 y 最小.
某校校长暑假将带领该校市级“三好生”去北京旅游.甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内,全部按全票价的6折(即按全票价的60%收费)优惠.”若全票价为240元.
(1)设学生数为 x,甲旅行社收费为 y甲,乙旅行社收费为 y乙,分别计算两家旅行社的收费(写出函数解析式);
做一做
当x < 4时,甲旅行社优惠;当x > 4时,乙旅行社优惠.
(2)当学生数是多少时,两家旅行社的收费一样?
(3)就学生数讨论哪家旅行社更优惠.
当x = 4时,两家旅行社的收费一样.
1.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.
>1500
当堂练习
2. 某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少?
解法一:设该单位参加旅游人数为x.那么选甲旅行社,应付费用80x 元;选乙旅行社,应付(60x+1000)元.记 y1= 80x,y2= 60x+1000.在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
观察图象,可知:当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49人时,选择甲旅行社费用较少;
当人数为51~100人时,选择乙旅行社费用较少.
x/人
50
60
y/元
800
1600
3200
2400
4000
4800
5600
O
10
20
30
40
70
80
90
y1= 80x
y2= 60x+1000
解法二:
(1)当y1=y2,即80x= 60x+1000时,x=50.
所以当人数为50时,选择甲或乙旅行社费用都一样;
(2)当y1 > y2,即80x > 60x+1000时, 得x > 50.
所以当人数为51~100人时 ,选择乙旅行社费用较少;
(3)当y1 < y2,即80x < 60x+1000时,得x<50.
所以当人数为0~49人时,选择甲旅行社费用较少;
解法三:设选择甲、乙旅行社费用之差为y,
则y=y1-y2=80x-(60x+1000)=20x-1000.
画出一次函数y= 20x-1000的图象如下图.
O
20
40
60
-200
-400
-600
-800
-1000
y
x
y= 20x-1000
它与x轴交点为(50,0) 由图可知:
(1)当x=50时,y=0,即y1=y2;
(2)当x>50时,y > 0,即y1 > y2;
(3)当x<50时,y <0,即y1 < y2.
课堂小结
实际问题
函数问题
设变量
找对应关系
函数问题的解
实际问题的解
解释实际意义
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
