19.2.2 一次函数的概念 课件(共23张PPT)
文档属性
| 名称 | 19.2.2 一次函数的概念 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 20:28:37 | ||
图片预览








文档简介
(共23张PPT)
2022年春人教版数学
八年级下册数学精品课件
19.2.2 一次函数
第1课时 一次函数的概念
第十九章 一次函数
情境引入
1.理解一次函数的概念,明确一次函数与正比例函数之间的联系.
2.能利用一次函数解决简单的实际问题.(重点、难点)
学习目标
某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃.登山队员由大本营向上登高x km时,他们所在位置的气温是y℃.试用函数解析式表示y与x的关系.
反思:这个函数是正比例函数吗?它与正比例函数有什么不同?这种形式的函数还会有吗?
y=5-6x
导入新课
问题1
一次函数的概念
下列问题中,变量之间的对应关系是函数关系吗?
如果是,请写出函数解析式.
(1)有人发现,在20 ℃~25 ℃时蟋蟀每分鸣叫次数c 与温度 t(单位:℃)有关,且 c 的值约是 t 的7 倍与35的差;
(2)一种计算成年人标准体重G(单位:kg)的方法是,以厘米为单位量出身高值 h ,再减常数105,所得差是G 的值;
(20≤t≤25)
问题2
讲授新课
(3)某城市的市内电话的月收费额 y(单位:元)包括月租费22元和拨打电话 x min 的计时费(按0.1元/min收取);
(4)把一个长10 cm,宽5 cm的矩形的长减少 x cm,宽不变,矩形面积 y(单位:cm2)随x的值而变化.
(0≤x≤10)
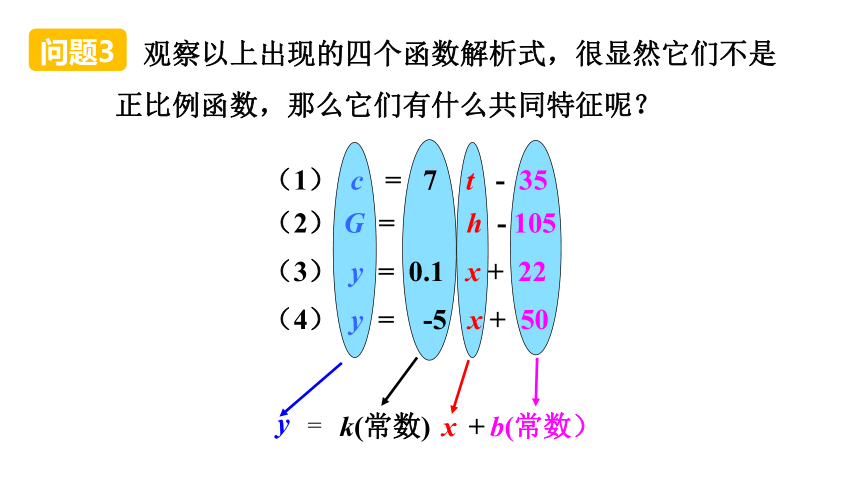
观察以上出现的四个函数解析式,很显然它们不是正比例函数,那么它们有什么共同特征呢?
y
k(常数)
x
=
b(常数)
+
(1) c = 7 t - 35
(2) G = h - 105
(3) y = 0.1 x + 22
(4) y = -5 x + 50
问题3
一般地,形如y=kx+b (k, b 是常数,k≠0)的函数,叫做一次函数.
思考:一次函数与正比例函数有什么关系?
(2)正比例函数是一种特殊的一次函数.
(1)当b=0时,y=kx+b 即y=kx(k≠0),此时该一次函数是正比例函数.
知识要点
(7) ;
下列函数中哪些是一次函数,哪些又是正比例函数?
(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) ;
(8) .
解:(1)(4)(5)(7)(8)是一次函数,
(1)是正比例函数
练一练
已知函数y=(m-1)x+1-m2
(2)当m为何值时,这个函数是正比例函数
(1)当m为何值时,这个函数是一次函数
解:(1)由题意可得
m-1≠0,解得m≠1.
(2)由题意可得
m-1≠0,1-m2=0,解得m=-1.
即m≠1时,这个函数是一次函数.
即m=-1时,这个函数是正比例函数.
典例精析
例1
已知一次函数 y=kx+b,当 x=1时,y=5;当x=-1时,
y=1.求 k 和 b 的值.
解:因为当x=1时,y=5;当x=-1时,y=1
所以
解得 k=2,b=3.
例2
我国现行个人工资、薪金所得税征收办法规定:月收入低于3500元的部分不收税;月收入超过3500元但低于5000元的部分征收3%的所得税……如某人月收入3860元,他应缴个人工资、薪金所得税为:(3860-3500)×3%=10.8元.
(1)当月收入大于3500元而又小于5000元时,写出应缴所得税y(元)与收入x(元)之间的函数解析式.
解:y=0.03×(x-3 500) (3500一次函数的简单应用
例3
(2)某人月收入为4160元,他应缴所得税多少元?
解:当x=4160时,y=0.03×(4160-3500)=19.8(元).
解:设此人本月工资是x元,
则 19.2=0.03×(x-3500), x=4140.
答:此人本月工资是4140元.
(3)如果某人本月应缴所得税19.2元,那么此人本月工资是多少元?
如图,△ABC是边长为x的等边三角形.
(1)求BC边上的高h与x之间的函数解析式.h是x的
一次函数吗?如果是,请指出相应的k与b的值.
解: (1)因为BC边上的高AD也是BC边上的中线,所以,BD=x/2.在Rt△ABD中,由勾股定理,得
即
所以h是x的一次函数,且
例4
(2)当h= 时,求x的值.
(3)求△ABC的面积S与x的函数解析式.S是x的一次函数吗?
解:
(2)当h= 时,有 .
解得x=2.
(3)因为
即 所以,S不是x的一次函数.
如果等腰三角形的周长是20cm,底边长是xcm,那么,腰长y(cm)与底边长x(cm)之间的函数解析式是什么?这个函数是一次函数吗?
解:y=10- x,是一次函数.
做一做
当堂练习
1.下列说法正确的是( )
A.一次函数是正比例函数.
B.正比例函数不是一次函数.
C.不是正比例函数就不是一次函数.
D.正比例函数是一次函数.
D
2.在函数①y=2-x,②y=8+0.03t,③y=1+x+ , ④y= 中,是一次函数的有_________.
①②
3.在函数y=(m-2)x+(m2-4)中,当m 时,y是x的一次函数;当m 时,y是x的正比例函数.
≠2
=-2
4.一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加2 m/s.
(1)求小球速度v(单位:m/s)
关于时间t(单位:s)的函数解析式.
它是一次函数吗?
(2)求第2.5 s 时小球的速度;
(3)时间每增加1 s,速度增加多少,速度增加量是否随着时间的变化而变化?
解:(1)小球速度v关于时间t的函数解析式为v=2t,是一次函数.
(2)当t=2.5时,v=2×2.5=5(m/s).
(3)时间每增加1 s,速度增加2 m/s,速度增加量不随着时间的变化而变化.
课堂小结
一次函数的概念
形式:y=kx+b(k≠0)
特别地,当b=0时,y=kx(k≠0)是正比例函数
一次函数的简单应用
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
八年级下册数学精品课件
19.2.2 一次函数
第1课时 一次函数的概念
第十九章 一次函数
情境引入
1.理解一次函数的概念,明确一次函数与正比例函数之间的联系.
2.能利用一次函数解决简单的实际问题.(重点、难点)
学习目标
某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃.登山队员由大本营向上登高x km时,他们所在位置的气温是y℃.试用函数解析式表示y与x的关系.
反思:这个函数是正比例函数吗?它与正比例函数有什么不同?这种形式的函数还会有吗?
y=5-6x
导入新课
问题1
一次函数的概念
下列问题中,变量之间的对应关系是函数关系吗?
如果是,请写出函数解析式.
(1)有人发现,在20 ℃~25 ℃时蟋蟀每分鸣叫次数c 与温度 t(单位:℃)有关,且 c 的值约是 t 的7 倍与35的差;
(2)一种计算成年人标准体重G(单位:kg)的方法是,以厘米为单位量出身高值 h ,再减常数105,所得差是G 的值;
(20≤t≤25)
问题2
讲授新课
(3)某城市的市内电话的月收费额 y(单位:元)包括月租费22元和拨打电话 x min 的计时费(按0.1元/min收取);
(4)把一个长10 cm,宽5 cm的矩形的长减少 x cm,宽不变,矩形面积 y(单位:cm2)随x的值而变化.
(0≤x≤10)
观察以上出现的四个函数解析式,很显然它们不是正比例函数,那么它们有什么共同特征呢?
y
k(常数)
x
=
b(常数)
+
(1) c = 7 t - 35
(2) G = h - 105
(3) y = 0.1 x + 22
(4) y = -5 x + 50
问题3
一般地,形如y=kx+b (k, b 是常数,k≠0)的函数,叫做一次函数.
思考:一次函数与正比例函数有什么关系?
(2)正比例函数是一种特殊的一次函数.
(1)当b=0时,y=kx+b 即y=kx(k≠0),此时该一次函数是正比例函数.
知识要点
(7) ;
下列函数中哪些是一次函数,哪些又是正比例函数?
(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) ;
(8) .
解:(1)(4)(5)(7)(8)是一次函数,
(1)是正比例函数
练一练
已知函数y=(m-1)x+1-m2
(2)当m为何值时,这个函数是正比例函数
(1)当m为何值时,这个函数是一次函数
解:(1)由题意可得
m-1≠0,解得m≠1.
(2)由题意可得
m-1≠0,1-m2=0,解得m=-1.
即m≠1时,这个函数是一次函数.
即m=-1时,这个函数是正比例函数.
典例精析
例1
已知一次函数 y=kx+b,当 x=1时,y=5;当x=-1时,
y=1.求 k 和 b 的值.
解:因为当x=1时,y=5;当x=-1时,y=1
所以
解得 k=2,b=3.
例2
我国现行个人工资、薪金所得税征收办法规定:月收入低于3500元的部分不收税;月收入超过3500元但低于5000元的部分征收3%的所得税……如某人月收入3860元,他应缴个人工资、薪金所得税为:(3860-3500)×3%=10.8元.
(1)当月收入大于3500元而又小于5000元时,写出应缴所得税y(元)与收入x(元)之间的函数解析式.
解:y=0.03×(x-3 500) (3500
例3
(2)某人月收入为4160元,他应缴所得税多少元?
解:当x=4160时,y=0.03×(4160-3500)=19.8(元).
解:设此人本月工资是x元,
则 19.2=0.03×(x-3500), x=4140.
答:此人本月工资是4140元.
(3)如果某人本月应缴所得税19.2元,那么此人本月工资是多少元?
如图,△ABC是边长为x的等边三角形.
(1)求BC边上的高h与x之间的函数解析式.h是x的
一次函数吗?如果是,请指出相应的k与b的值.
解: (1)因为BC边上的高AD也是BC边上的中线,所以,BD=x/2.在Rt△ABD中,由勾股定理,得
即
所以h是x的一次函数,且
例4
(2)当h= 时,求x的值.
(3)求△ABC的面积S与x的函数解析式.S是x的一次函数吗?
解:
(2)当h= 时,有 .
解得x=2.
(3)因为
即 所以,S不是x的一次函数.
如果等腰三角形的周长是20cm,底边长是xcm,那么,腰长y(cm)与底边长x(cm)之间的函数解析式是什么?这个函数是一次函数吗?
解:y=10- x,是一次函数.
做一做
当堂练习
1.下列说法正确的是( )
A.一次函数是正比例函数.
B.正比例函数不是一次函数.
C.不是正比例函数就不是一次函数.
D.正比例函数是一次函数.
D
2.在函数①y=2-x,②y=8+0.03t,③y=1+x+ , ④y= 中,是一次函数的有_________.
①②
3.在函数y=(m-2)x+(m2-4)中,当m 时,y是x的一次函数;当m 时,y是x的正比例函数.
≠2
=-2
4.一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加2 m/s.
(1)求小球速度v(单位:m/s)
关于时间t(单位:s)的函数解析式.
它是一次函数吗?
(2)求第2.5 s 时小球的速度;
(3)时间每增加1 s,速度增加多少,速度增加量是否随着时间的变化而变化?
解:(1)小球速度v关于时间t的函数解析式为v=2t,是一次函数.
(2)当t=2.5时,v=2×2.5=5(m/s).
(3)时间每增加1 s,速度增加2 m/s,速度增加量不随着时间的变化而变化.
课堂小结
一次函数的概念
形式:y=kx+b(k≠0)
特别地,当b=0时,y=kx(k≠0)是正比例函数
一次函数的简单应用
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
