19.2.2 一次函数与实际问题 课件(共25张PPT)
文档属性
| 名称 | 19.2.2 一次函数与实际问题 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-16 20:14:37 | ||
图片预览





文档简介
(共25张PPT)
2022年春人教版数学
八年级下册数学精品课件
19.2.2 一次函数
第4课时 一次函数与实际问题
第十九章 一次函数
情境引入
1.巩固一次函数知识,灵活运用变量关系解决相关实际问题;
2.有机地把各种数学模型通过函数统一起来使用,提高解决实
际问题的能力;(重点)
3.认识数学在现实生活中的意义,提高运用数学知识解决实际
问题的能力.(难点)
学习目标
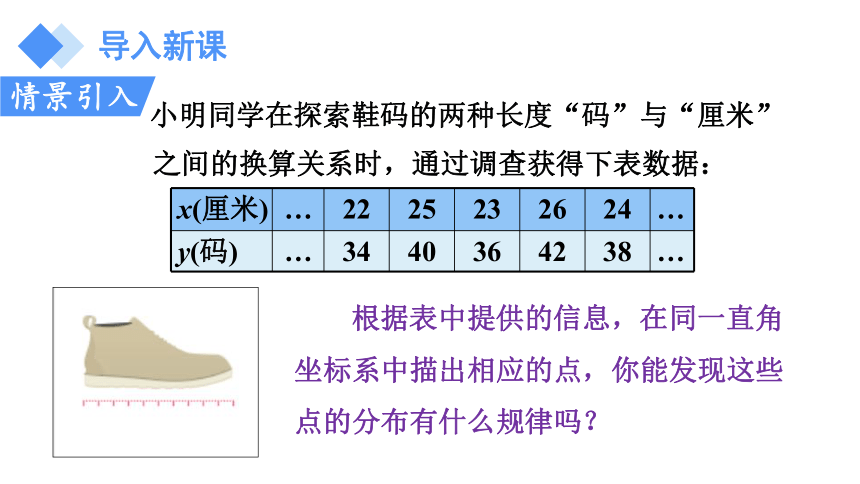
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
x(厘米) … 22 25 23 26 24 …
y(码) … 34 40 36 42 38 …
根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
导入新课
情景引入
30
32
38
36
34
42
40
23
25
24
21
22
27
26
y (码)
x(厘米)
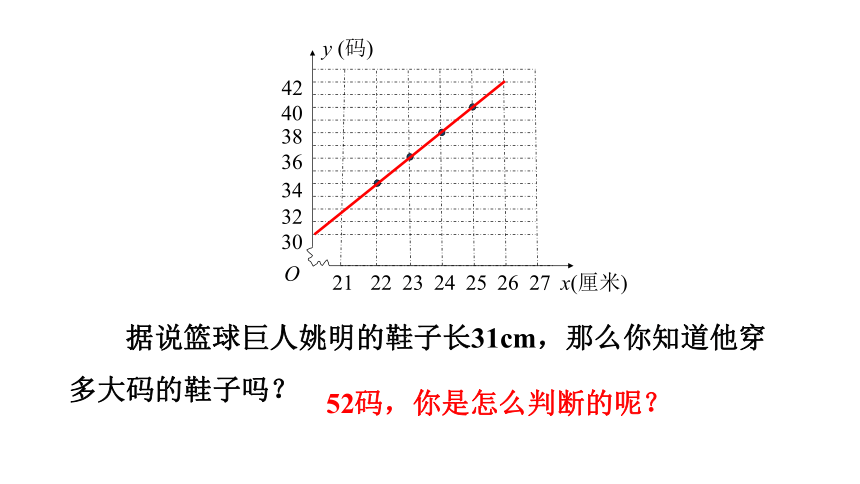
据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?
52码,你是怎么判断的呢?
O
一次函数与实际问题
购买种子
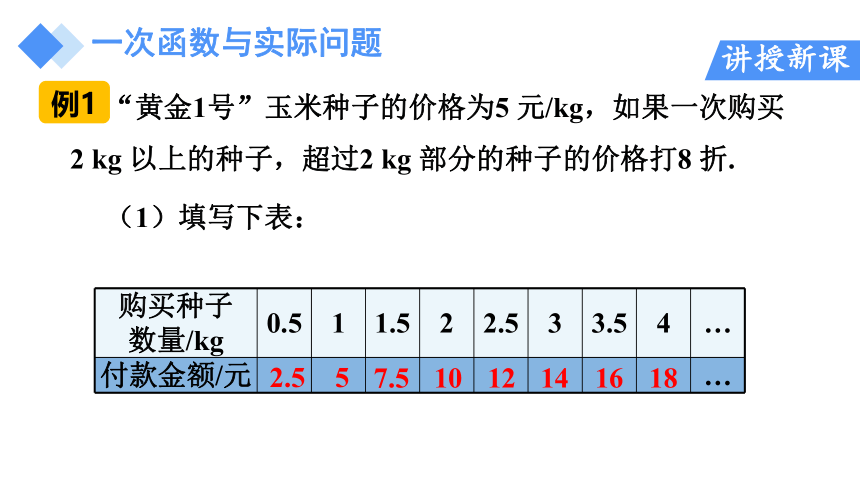
数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
“黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
例1
讲授新课
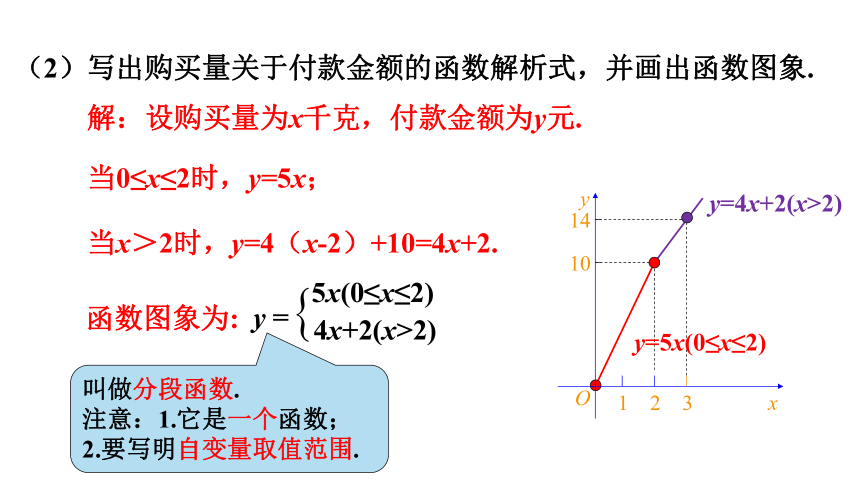
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为: .
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
y =
5x(0≤x≤2)
4x+2(x>2)
函数图象为:
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
你能由上面的函数解析式或函数图象解决以下问题吗?
(1)一次购买1.5 kg 种子,需付款多少元?
(2)30元最多能购买多少种子?
思考
为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
分析:
(1)x≤8时,每立方米收费(1+0.3)元;
(2)x>8时,超过的部分每立方米收费(1.5+1.2)元.
例2
解:(1)y关于x的函数解析式为:
(1+0.3)x =1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2. (x>8)
y=
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)因为1.3×8=10.4<26.6,所以该用户用水量超过8立方米.
所以2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14吨.
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)服药后______时,血液中含药量最高,达到每毫升_______毫克,接着逐步衰弱.
(2)服药5时,血液中含药量为
每毫升____毫克.
x/时
y/毫克
6
3
2
5
O
2
6
3
做一做
(3)当x≤2时y与x之间的函数解析式是___________.
(4)当x≥2时y与x之间的函数解析式是___________.
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是______时.
y=3x
y=-x+8
4
x/时
y/毫克
6
3
2
5
O
百舸竞渡,激情飞扬,端午节期间,某地举行龙舟比赛.甲、乙两支龙舟队在比赛时路程y(米)与时间x(分钟)之间的函数图象如图.根据图象回答下列问题:
(1)1.8分钟时,哪支龙舟队处于领先位置?
(2)在这次龙舟赛中,哪支龙舟队先到达终点?提前多少时间到达?
(3)求乙队加速后,路程y(米)
与时间x(分钟)之间的函数解析式.
300
O
1
2
3
4
600
1050
150
5
4.5
乙
甲
y(米)
x(分钟)
例3
(1)(2)观察图象可得.(3)用待定系数法解.
解:由图象,可知
(1)1.8分钟时甲龙舟队处于领先位置.
(2)在这次龙舟赛中,乙龙舟队先到达终点,比甲提前0.5分钟.
(3)设乙队加速后,y与x的函数解析式为y=kx+b.
将(2,300)、(4.5,1050)分别代入上式,
得 解得
∴ y = 300x-300(2≤x≤4.5)
300
O
1
2
3
4
600
1050
150
5
4.5
乙
甲
y(米)
x(分)
分析
解:(1)由题意得
当0≤t≤2时,T=20;
当2函数解析式为:
T =
20(0≤t≤2)
5t+10(2T=20(0≤t≤2)
T=5t+10(220
10
40
T/℃
t/h
O
1
2
30
4
3
(2)函数图像为:
1.一个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
当堂练习
2. 全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源已经成为一项十分紧迫的任务,某地区现有土地100万平方千米,沙漠200万平方千米,土地沙漠化的变化情况如下图所示.
(1)如果不采取任何措施,那么到第5年底,该地区沙漠面积将增加多少万千米2?
10万千米2
(2)如果该地区沙漠的面积继续按此趋势扩大,那么从现在开始,第几年底后,该地区将丧失土地资源?
(3)如果从现在开始采取植树造林措施,每年改造4万千米2
沙漠,那么到第几年底,该地区的沙漠面积能减少到176万千米2.
每年新增面积为2万千米2,所以第50年底后将丧失土地资源.
第12年底
3.近几年来,由于经济和社会发展迅速,用电量越来越多.
为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
25
50
75
100
25
50
70
100
O
y(元)
x(度)
75
⑴请你根据图象所描述的信息,分别求出当0≤x≤50 和x>50时,y与x的函数解析式;
解:当0≤x≤50 时,由图象可设 y=k1x,
∵其经过(50,25),代入得25=50k1,∴k1=0.5,∴y=0.5x ;
当x>50时,由图象可设 y=k2x+b,
∵其经过(50,25)、(100,70),
得k2=0.9,b=-20,∴y=0.9x-20.
25
50
75
100
25
50
70
100
O
y(元)
x(度)
75
⑵根据你的分析:当每月用电量不超过50度时,收费标准是多少?当每月用电量超过50度时,收费标准是多少?
解:不超过50度部分按0.5元/度计算,超过部分按0.9元/度计算.
25
50
75
100
25
50
70
100
O
y(元)
x(度)
75
课堂小结
一次函数与实际问题
一次函数的图象与实际问题
分段函数的解析式与图象
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
八年级下册数学精品课件
19.2.2 一次函数
第4课时 一次函数与实际问题
第十九章 一次函数
情境引入
1.巩固一次函数知识,灵活运用变量关系解决相关实际问题;
2.有机地把各种数学模型通过函数统一起来使用,提高解决实
际问题的能力;(重点)
3.认识数学在现实生活中的意义,提高运用数学知识解决实际
问题的能力.(难点)
学习目标
小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
x(厘米) … 22 25 23 26 24 …
y(码) … 34 40 36 42 38 …
根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
导入新课
情景引入
30
32
38
36
34
42
40
23
25
24
21
22
27
26
y (码)
x(厘米)
据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?
52码,你是怎么判断的呢?
O
一次函数与实际问题
购买种子
数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
“黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
例1
讲授新课
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为: .
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
y =
5x(0≤x≤2)
4x+2(x>2)
函数图象为:
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
你能由上面的函数解析式或函数图象解决以下问题吗?
(1)一次购买1.5 kg 种子,需付款多少元?
(2)30元最多能购买多少种子?
思考
为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
分析:
(1)x≤8时,每立方米收费(1+0.3)元;
(2)x>8时,超过的部分每立方米收费(1.5+1.2)元.
例2
解:(1)y关于x的函数解析式为:
(1+0.3)x =1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2. (x>8)
y=
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)因为1.3×8=10.4<26.6,所以该用户用水量超过8立方米.
所以2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14吨.
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)服药后______时,血液中含药量最高,达到每毫升_______毫克,接着逐步衰弱.
(2)服药5时,血液中含药量为
每毫升____毫克.
x/时
y/毫克
6
3
2
5
O
2
6
3
做一做
(3)当x≤2时y与x之间的函数解析式是___________.
(4)当x≥2时y与x之间的函数解析式是___________.
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是______时.
y=3x
y=-x+8
4
x/时
y/毫克
6
3
2
5
O
百舸竞渡,激情飞扬,端午节期间,某地举行龙舟比赛.甲、乙两支龙舟队在比赛时路程y(米)与时间x(分钟)之间的函数图象如图.根据图象回答下列问题:
(1)1.8分钟时,哪支龙舟队处于领先位置?
(2)在这次龙舟赛中,哪支龙舟队先到达终点?提前多少时间到达?
(3)求乙队加速后,路程y(米)
与时间x(分钟)之间的函数解析式.
300
O
1
2
3
4
600
1050
150
5
4.5
乙
甲
y(米)
x(分钟)
例3
(1)(2)观察图象可得.(3)用待定系数法解.
解:由图象,可知
(1)1.8分钟时甲龙舟队处于领先位置.
(2)在这次龙舟赛中,乙龙舟队先到达终点,比甲提前0.5分钟.
(3)设乙队加速后,y与x的函数解析式为y=kx+b.
将(2,300)、(4.5,1050)分别代入上式,
得 解得
∴ y = 300x-300(2≤x≤4.5)
300
O
1
2
3
4
600
1050
150
5
4.5
乙
甲
y(米)
x(分)
分析
解:(1)由题意得
当0≤t≤2时,T=20;
当2
T =
20(0≤t≤2)
5t+10(2
T=5t+10(2
10
40
T/℃
t/h
O
1
2
30
4
3
(2)函数图像为:
1.一个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
当堂练习
2. 全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源已经成为一项十分紧迫的任务,某地区现有土地100万平方千米,沙漠200万平方千米,土地沙漠化的变化情况如下图所示.
(1)如果不采取任何措施,那么到第5年底,该地区沙漠面积将增加多少万千米2?
10万千米2
(2)如果该地区沙漠的面积继续按此趋势扩大,那么从现在开始,第几年底后,该地区将丧失土地资源?
(3)如果从现在开始采取植树造林措施,每年改造4万千米2
沙漠,那么到第几年底,该地区的沙漠面积能减少到176万千米2.
每年新增面积为2万千米2,所以第50年底后将丧失土地资源.
第12年底
3.近几年来,由于经济和社会发展迅速,用电量越来越多.
为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
25
50
75
100
25
50
70
100
O
y(元)
x(度)
75
⑴请你根据图象所描述的信息,分别求出当0≤x≤50 和x>50时,y与x的函数解析式;
解:当0≤x≤50 时,由图象可设 y=k1x,
∵其经过(50,25),代入得25=50k1,∴k1=0.5,∴y=0.5x ;
当x>50时,由图象可设 y=k2x+b,
∵其经过(50,25)、(100,70),
得k2=0.9,b=-20,∴y=0.9x-20.
25
50
75
100
25
50
70
100
O
y(元)
x(度)
75
⑵根据你的分析:当每月用电量不超过50度时,收费标准是多少?当每月用电量超过50度时,收费标准是多少?
解:不超过50度部分按0.5元/度计算,超过部分按0.9元/度计算.
25
50
75
100
25
50
70
100
O
y(元)
x(度)
75
课堂小结
一次函数与实际问题
一次函数的图象与实际问题
分段函数的解析式与图象
课后作业
1、完成课本练习题。
2、完成练习册本课习题。
https://www.21cnjy.com/help/help_extract.php
