高一数学人教A版(2019)必修第一册(学案)三角函数的图象与性质 (含答案)
文档属性
| 名称 | 高一数学人教A版(2019)必修第一册(学案)三角函数的图象与性质 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 171.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 00:00:00 | ||
图片预览



文档简介
三角函数的图象与性质——正弦函数、余弦函数的图象
【知识梳理】
1.正弦曲线、余弦曲线
(1)定义:正弦函数)和余弦函数的图像分别叫做_____曲线和_____曲线。
(2)图像:如图所示。
2.“五点法”画图
步骤:
(1)列表:
x 0 π 2π
sinx 0 1 0 -1 0
cosx 1 0 -1 0 1
(2)描点:
画正弦函数y=sinx,x∈[0,2π]的图像,五个关键点是_____;画余弦函数y=cosx,x∈[0,2π]的图像,五个关键点是_____。
(3)用光滑曲线顺次连接这五个点,得到正、余弦曲线的简图。
3.正、余弦曲线的联系
依据诱导公式cosx=sin,要得到y=cosx的图像,只需把y=sinx的图像向_____平移个单位长度即可。
【自主探究】
已知0≤x≤2π,结合正、余弦曲线试探究sinx与cosx的大小关系。
【对点讲练】
知识点一:利用“五点法”作正、余弦函数的图像
例1:利用“五点法”画函数y=-sinx+1(0≤x≤2π)的简图。
回顾归纳:作正弦、余弦曲线要理解几何法作图,掌握五点法作图。“五点”即y=sinx或y=cosx的图像在一个最小正周期内的最高点、最低点和与x轴的交点。“五点法”是作简图的常用方法。
变式训练1:利用“五点法”画函数y=-1-cosx,x∈[0,2π]的简图。
知识点二:利用三角函数图像求定义域
例2:求函数f(x)=lgsinx+的定义域。
回顾归纳 一些三角函数的定义域可以借助函数图像直观地观察得到,同时要注意区间端点的取舍。
变式训练2:求函数f(x)=+lg(8x-x2)的定义域。
知识点三:利用三角函数的图像判断方程解的个数
例3:在同一坐标系中,作函数y=sinx和y=lgx的图像,根据图像判断出方程sinx=lgx的解的个数。
回顾归纳:三角函数的图像是研究函数的重要工具,通过图像可较简便的解决问题,这正是数形结合思想方法的应用。
变式训练3:求方程x2=cosx的实数解的个数。
【课堂小结】
1.正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础。
2.五点法是画三角函数图像的基本方法,要熟练掌握,与五点法作图有关的问题是高考常考知识点之一、
【课时作业】
一、选择题。
1.函数y=sinx(x∈R)图像的一条对称轴是( )
A.x轴 B.y轴
C.直线y=x D.直线x=
2.函数y=-cosx的图像与余弦函数y=cosx的图像( )
A.只关于x轴对称 B.关于原点对称
C.关于原点、x轴对称 D.关于原点、坐标轴对称
3.如果x∈[0,2π],则函数y=+的定义域为( )
A.[0,π] B.
C. D.
4.在(0,2π)内使sinx>|cosx|的x的取值范围是( )
A. B.∪
C. D.
5.已知函数y=2sinx的图像与直线y=2围成一个封闭的平面图形,那么此封闭图形的面积( )
A.4 B.8 C.4π D.2π
二、填空题。
6.函数y=的定义域为_____。
7.函数y=的定义域是_____。
8.设0≤x≤2π,且|cosx-sinx|=sinx-cosx,则x的取值范围为_____。
三、解答题
9.利用“五点法”作出下列函数的简图:
(1)y=-sinx(0≤x≤2π);(2)y=1+cos x(0≤x≤2π)。
10.分别作出下列函数的图像。
(1)y=|sinx|,x∈R;(2)y=sin|x|,x∈R。
答案
知识梳理
1.(1)正弦 余弦
2.(2)(0,0),,(π,0),,(2π,0)
(0,1),,(π,-1),,(2π,1)
3.左
自主探究
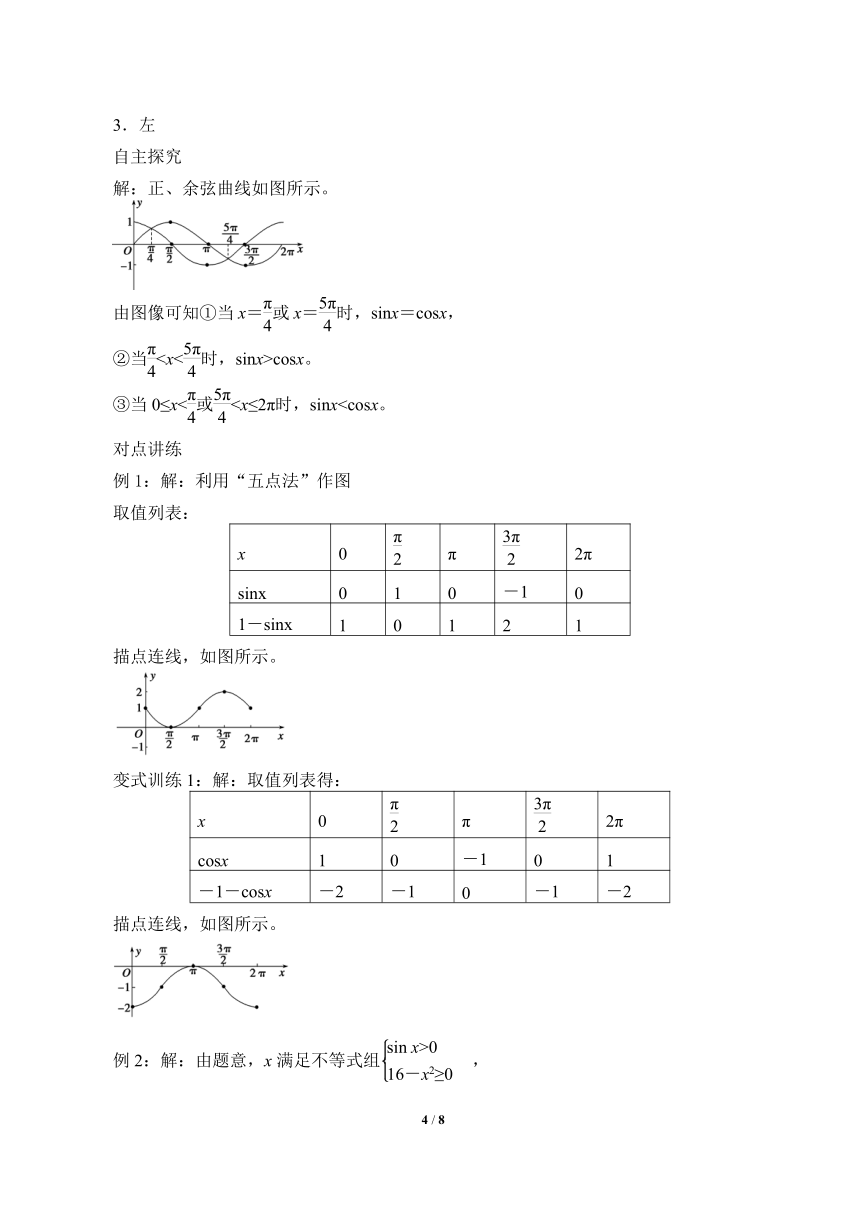
解:正、余弦曲线如图所示。
由图像可知①当x=或x=时,sinx=cosx,
②当cosx。
③当0≤x<或对点讲练
例1:解:利用“五点法”作图
取值列表:
x 0 π 2π
sinx 0 1 0 -1 0
1-sinx 1 0 1 2 1
描点连线,如图所示。
变式训练1:解:取值列表得:
x 0 π 2π
cosx 1 0 -1 0 1
-1-cosx -2 -1 0 -1 -2
描点连线,如图所示。
例2:解:由题意,x满足不等式组,
即,作出y=sinx的图像,如图所示。
结合图像可得:x∈[-4,-π)∪(0,π)。
变式训练2:解:由,得。
画出y=cosx,x∈[0,3π]的图像,如图所示。
结合图像可得:x∈∪。
例3 解 建立坐标系xOy,先用五点法画出函数y=sinx,x∈[0,2π]的图像,再依次向左、右连续平移2π个单位,得到y=sin x的图像。
描出点,(1,0),(10,1)并用光滑曲线连接得到y=lgx的图像,如图所示。
由图像可知方程sinx=lgx的解有3个。
变式训练3:解:作函数y=cosx与y=x2的图像,如图所示,
由图像,可知原方程有两个实数解。
课时作业
1.D
2.C (结合图像易知)
3.C (∵sin x≥0且-cos x≥0,∴x∈。)
4.A
(∵sinx>|cosx|,
∴sinx>0,∴x∈(0,π),在同一坐标系中画出y=sinx,x∈(0,π)与y=|cosx|,
x∈(0,π)的图像,观察图像易得x∈。)
5.C (数形结合,如图所示。
y=2sinx,x∈的图像与直线y=2围成的封闭平面图形面积相当于由x=,x=,y=0,y=2围成的矩形面积,即S=×2=4π。)
6.(k∈Z)
解析:x应满足:
综合正、余弦函数图像可知:
-+2kπ7.,(k∈Z)
解析:由2cosx+1≥0,得cosx≥-,
∴2kπ-≤x≤2kπ+,k∈Z。
8.
解析:由题意知sinx-cosx≥0,即cosx≤sinx,在同一坐标系画出y=sinx,x∈[0,2π]
与y=cosx,x∈[0,2π]的图像,如图所示:
观察图像得:≤x≤。
9.解:利用“五点法”作图。
(1)列表:
x 0 π 2π
sin x 0 1 0 -1 0
-sin x 0 -1 0 1 0
描点作图,如图所示。
(2)列表:
x 0 π 2π
cos x 1 0 -1 0 1
1+cos x 2 1 0 1 2
描点作图,如图所示。
10.解:(1)y=|sinx|=(k∈Z)。
其图像如图所示,
(2)y=sin|x|=,
其图像如图所示,
4 / 7
【知识梳理】
1.正弦曲线、余弦曲线
(1)定义:正弦函数)和余弦函数的图像分别叫做_____曲线和_____曲线。
(2)图像:如图所示。
2.“五点法”画图
步骤:
(1)列表:
x 0 π 2π
sinx 0 1 0 -1 0
cosx 1 0 -1 0 1
(2)描点:
画正弦函数y=sinx,x∈[0,2π]的图像,五个关键点是_____;画余弦函数y=cosx,x∈[0,2π]的图像,五个关键点是_____。
(3)用光滑曲线顺次连接这五个点,得到正、余弦曲线的简图。
3.正、余弦曲线的联系
依据诱导公式cosx=sin,要得到y=cosx的图像,只需把y=sinx的图像向_____平移个单位长度即可。
【自主探究】
已知0≤x≤2π,结合正、余弦曲线试探究sinx与cosx的大小关系。
【对点讲练】
知识点一:利用“五点法”作正、余弦函数的图像
例1:利用“五点法”画函数y=-sinx+1(0≤x≤2π)的简图。
回顾归纳:作正弦、余弦曲线要理解几何法作图,掌握五点法作图。“五点”即y=sinx或y=cosx的图像在一个最小正周期内的最高点、最低点和与x轴的交点。“五点法”是作简图的常用方法。
变式训练1:利用“五点法”画函数y=-1-cosx,x∈[0,2π]的简图。
知识点二:利用三角函数图像求定义域
例2:求函数f(x)=lgsinx+的定义域。
回顾归纳 一些三角函数的定义域可以借助函数图像直观地观察得到,同时要注意区间端点的取舍。
变式训练2:求函数f(x)=+lg(8x-x2)的定义域。
知识点三:利用三角函数的图像判断方程解的个数
例3:在同一坐标系中,作函数y=sinx和y=lgx的图像,根据图像判断出方程sinx=lgx的解的个数。
回顾归纳:三角函数的图像是研究函数的重要工具,通过图像可较简便的解决问题,这正是数形结合思想方法的应用。
变式训练3:求方程x2=cosx的实数解的个数。
【课堂小结】
1.正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础。
2.五点法是画三角函数图像的基本方法,要熟练掌握,与五点法作图有关的问题是高考常考知识点之一、
【课时作业】
一、选择题。
1.函数y=sinx(x∈R)图像的一条对称轴是( )
A.x轴 B.y轴
C.直线y=x D.直线x=
2.函数y=-cosx的图像与余弦函数y=cosx的图像( )
A.只关于x轴对称 B.关于原点对称
C.关于原点、x轴对称 D.关于原点、坐标轴对称
3.如果x∈[0,2π],则函数y=+的定义域为( )
A.[0,π] B.
C. D.
4.在(0,2π)内使sinx>|cosx|的x的取值范围是( )
A. B.∪
C. D.
5.已知函数y=2sinx的图像与直线y=2围成一个封闭的平面图形,那么此封闭图形的面积( )
A.4 B.8 C.4π D.2π
二、填空题。
6.函数y=的定义域为_____。
7.函数y=的定义域是_____。
8.设0≤x≤2π,且|cosx-sinx|=sinx-cosx,则x的取值范围为_____。
三、解答题
9.利用“五点法”作出下列函数的简图:
(1)y=-sinx(0≤x≤2π);(2)y=1+cos x(0≤x≤2π)。
10.分别作出下列函数的图像。
(1)y=|sinx|,x∈R;(2)y=sin|x|,x∈R。
答案
知识梳理
1.(1)正弦 余弦
2.(2)(0,0),,(π,0),,(2π,0)
(0,1),,(π,-1),,(2π,1)
3.左
自主探究
解:正、余弦曲线如图所示。
由图像可知①当x=或x=时,sinx=cosx,
②当
③当0≤x<或
例1:解:利用“五点法”作图
取值列表:
x 0 π 2π
sinx 0 1 0 -1 0
1-sinx 1 0 1 2 1
描点连线,如图所示。
变式训练1:解:取值列表得:
x 0 π 2π
cosx 1 0 -1 0 1
-1-cosx -2 -1 0 -1 -2
描点连线,如图所示。
例2:解:由题意,x满足不等式组,
即,作出y=sinx的图像,如图所示。
结合图像可得:x∈[-4,-π)∪(0,π)。
变式训练2:解:由,得。
画出y=cosx,x∈[0,3π]的图像,如图所示。
结合图像可得:x∈∪。
例3 解 建立坐标系xOy,先用五点法画出函数y=sinx,x∈[0,2π]的图像,再依次向左、右连续平移2π个单位,得到y=sin x的图像。
描出点,(1,0),(10,1)并用光滑曲线连接得到y=lgx的图像,如图所示。
由图像可知方程sinx=lgx的解有3个。
变式训练3:解:作函数y=cosx与y=x2的图像,如图所示,
由图像,可知原方程有两个实数解。
课时作业
1.D
2.C (结合图像易知)
3.C (∵sin x≥0且-cos x≥0,∴x∈。)
4.A
(∵sinx>|cosx|,
∴sinx>0,∴x∈(0,π),在同一坐标系中画出y=sinx,x∈(0,π)与y=|cosx|,
x∈(0,π)的图像,观察图像易得x∈。)
5.C (数形结合,如图所示。
y=2sinx,x∈的图像与直线y=2围成的封闭平面图形面积相当于由x=,x=,y=0,y=2围成的矩形面积,即S=×2=4π。)
6.(k∈Z)
解析:x应满足:
综合正、余弦函数图像可知:
-+2kπ
解析:由2cosx+1≥0,得cosx≥-,
∴2kπ-≤x≤2kπ+,k∈Z。
8.
解析:由题意知sinx-cosx≥0,即cosx≤sinx,在同一坐标系画出y=sinx,x∈[0,2π]
与y=cosx,x∈[0,2π]的图像,如图所示:
观察图像得:≤x≤。
9.解:利用“五点法”作图。
(1)列表:
x 0 π 2π
sin x 0 1 0 -1 0
-sin x 0 -1 0 1 0
描点作图,如图所示。
(2)列表:
x 0 π 2π
cos x 1 0 -1 0 1
1+cos x 2 1 0 1 2
描点作图,如图所示。
10.解:(1)y=|sinx|=(k∈Z)。
其图像如图所示,
(2)y=sin|x|=,
其图像如图所示,
4 / 7
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
