2021-2022学年人教版九年级数学下册第29章投影与视图同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第29章投影与视图同步测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 299.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 17:00:14 | ||
图片预览

文档简介
第29章投影与视图同步测试卷 2021-2022学年人教版
九年级数学下册
一、单选题
1.下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是
A.(3)(1)(4)(2) B.(3)(2)(1)(4)
C.(3)(4)(1)(2) D.(2)(4)(1)(3)
2.发展工业是强国之梦的重要举措,如图所示零件的左视图是( )
A. B. C. D.
3.如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6 m的正方形.要使灯光能照射到整个舞台,则灯P的悬挂高度是( )
A.3m B.3m C.4m D.m
4.如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是14,则排球的直径是( )
A.7 cm B.14 cm C.21 cm D.21cm
5.一个空心的圆柱如图所示,那么它的主视图是()
A. B. C. D.
6.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向上远移时,圆形阴影的大小的变化情况是( )
A.越来越小 B.越来越大 C.大小不变 D.不能确定
7.在下面的四个几何体中,它们各自的主视图与左视图可能相同的是( )
A. B. C. D.
8.如图是某几何体的三视图,下列判断正确的是( )
A.几何体是圆柱体,高为2 B.几何体是圆锥体,高为2
C.几何体是圆柱体,半径为2 D.几何体是圆锥体,直径为2
9.下列四个几何体的俯视图中与众不同的是( )
A. B. C. D.
10.如图所示,当小人向建筑物A靠近时,在建筑物B上形成的盲区( )
A.变大
B.变小
C.不变
D.无法确定
二、填空题
11.墙壁CD上D处有一盏灯(如图),小明站在A处测得他的影长与身长相等,都为1.6m,他向墙壁走1m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD=____.
12.如图,电影胶片上每一个图片的规格为3.5 cm×3.5 cm,放映屏幕的规格为2 m×2 m,若放映机的光源S距胶片20 cm,那么光源S距屏幕___米时,放映的图像刚好布满整个屏幕.
13.圆柱的主视图是长方形,左视图是________形,俯视图是________形.
14.从正面和左面看到长方体的图形如图所示(单位:cm),则从其上面看到图形的面积是_____ cm2.
15.如图,小丽站在30米高的楼顶远眺前方的广场,15米处有一个高为5米的障碍物,那么离楼房________的范围内小丽看不见.
16.长方体的主视图、俯视图如图,则其左视图面积为________.
17.如图是由若干个棱长为1的小正方体组合而成的一个几何体的三视图,则这个几何体的表面积是________.
主视图 左视图 俯视图
18.直角坐标系内,身高为1.5米的小强面向y轴站在x轴上的点A(-10,0)处,他的前方5米处有一堵墙,已知墙高2米,则站立的小强观察y(y>0)轴时,盲区(视力达不到的地方)范围是________.
19.如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要______个小立方块.
三、解答题
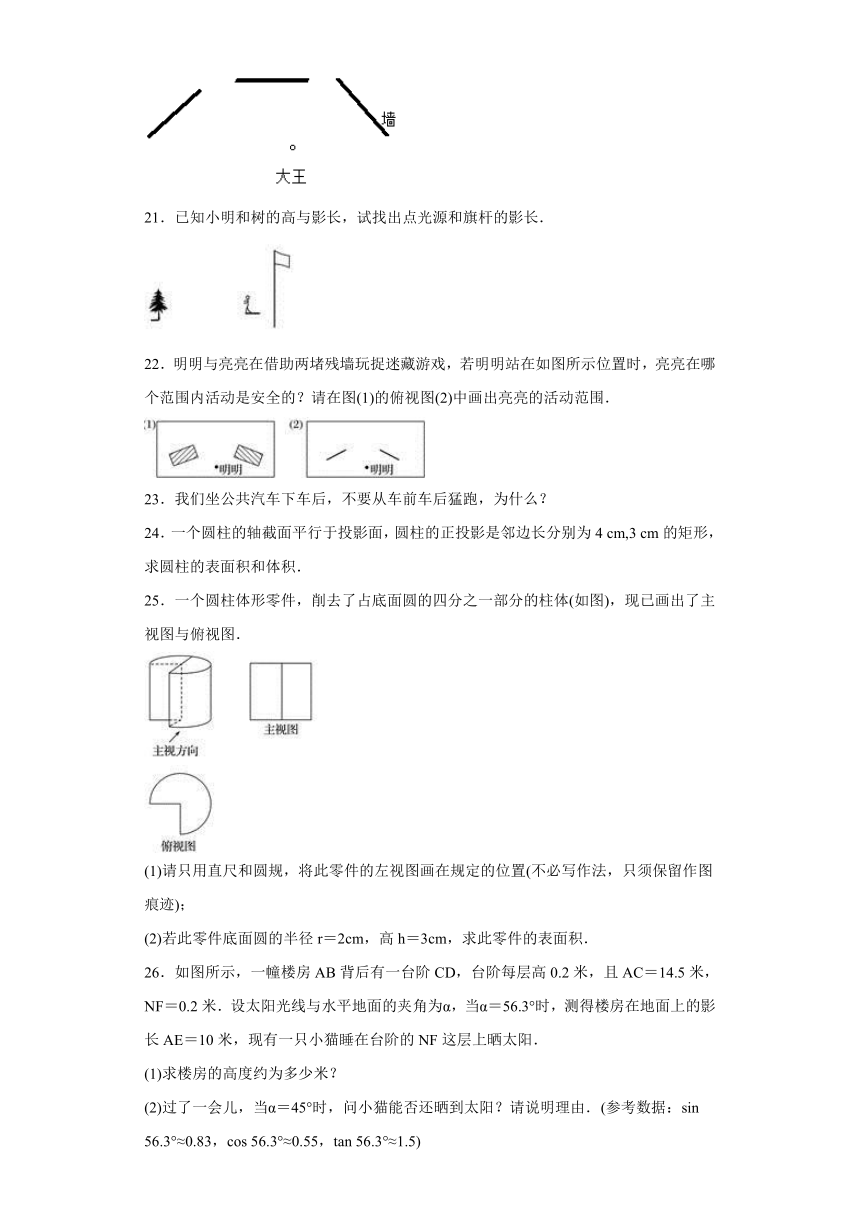
20.作图题: 如图所示:大王站在墙前,小明站在墙后,小明不能让大王看见,请你画出小明的活动区域.
21.已知小明和树的高与影长,试找出点光源和旗杆的影长.
22.明明与亮亮在借助两堵残墙玩捉迷藏游戏,若明明站在如图所示位置时,亮亮在哪个范围内活动是安全的?请在图(1)的俯视图(2)中画出亮亮的活动范围.
23.我们坐公共汽车下车后,不要从车前车后猛跑,为什么?
24.一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为4 cm,3 cm的矩形,求圆柱的表面积和体积.
25.一个圆柱体形零件,削去了占底面圆的四分之一部分的柱体(如图),现已画出了主视图与俯视图.
(1)请只用直尺和圆规,将此零件的左视图画在规定的位置(不必写作法,只须保留作图痕迹);
(2)若此零件底面圆的半径r=2cm,高h=3cm,求此零件的表面积.
26.如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin 56.3°≈0.83,cos 56.3°≈0.55,tan 56.3°≈1.5)
试卷第1页,共3页
参考答案:
1.C
【详解】
试题分析:根据从早晨到傍晚物体影子的指向是:西-西北-北-东北-东,影长由长变短,再变长,因此,
∵(1)为东北,(2)为东,(3)为西,(4)为西北,
∴将它们按时间先后顺序排列为(3)(4)(1)(2).
故选C.
2.D
【详解】
如图所示零件的左视图是.
故选D.
3.A
【详解】
连接AC,
∵∠APC=60°,
∴∠PAC=∠PCA=60°,
∵ABCD是边长为6m的正方形,
∴AC=6,OC=3
∴PC=6,
∴PO=3,
故选A.
4.C
【详解】
如图,点A与点B为太阳光线与球的切点,
则AB为排球的直径,CD=AB,cm,
在Rt△CDE中,sinE=
所以
即排球的直径为21cm.
故选C.
5.A
【详解】
根据主视图的定义,从前面看,得出图形是一个矩形(它里面含一个看不见的小矩形),即选项A的图形.
故选A.
6.A
【详解】
当点光源在物体上方,向下照射物体时,点光源离物体越近,影子越大,点光源离物体越远,影子越小.故圆形阴影越来越小.
故选A.
7.B
【详解】
A、此几何体主视图与左视图不相同,故此选项错误;
B、立方体的主视图与左视图都是矩形,故此选项正确;
B、三棱柱主视图是矩形,左视图也是矩形,矩形宽不相同,故此选项错误;
D、四棱柱的主视图是矩形,左视图也是矩形,矩形宽不相同,故此选项错误;
故选B.
8.A
【详解】
试题解析:根据主视图和左视图为矩形是柱体,根据俯视图是圆可判断出这个几何体应该是圆柱,
再根据左视图的高度得出圆柱体的高为2;
故选A.
9.B
【详解】
解:根据从上边看得到的图形是俯视图,可得
A的俯视图是第一列两个小正方形,第二列一个小正方形,
B的俯视图是第一列是两个小正方形,第二列是两个小正方形,
C的俯视图是第一列两个小正方形,第二列一个小正方形,
D的俯视图是第一列两个小正方形,第二列一个小正方形,
故选B.
10.A
【详解】
根据盲区即看不到的建筑物的高度.根据各物体的比例关系画出图形,数形结合,可以比较直观列出相关的比例关系式,从而得出答案.
解:如图所示:当小人向建筑物A靠近时,在建筑物B上形成的盲区不断增大,
故选A.
11.m
【详解】
如图:
根据题意得:BG=AF=AE=1.6m,AB=1m,
∵BG∥AF∥CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.6)m,AC=(x+1)m,
∴,
解得:x=, y=,
∴CD=m.
∴灯泡与地面的距离为米,
故答案为m.
12.
【详解】
运用位似图形的性质即可得;
设银幕距镜头xm,则有
,
解得:x=,
故答案为.
13.
【详解】
从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.
解:圆柱的主视图是长方形,左视图是长方形,俯视图是圆形.
本题考查了几何体的三视图的判断.
14.12
【详解】
根据从左面、从正面看到的形状图的相关数据可得:
从上面看到的形状图是长为4宽为3的长方形,
则从其上面看到图形的面积是4×3=12;
故答案为12.
15.15~18
【详解】
先判断出盲区,然后利用解直角三角形的知识求出盲区即可.
解:由题意得,盲区为BD,
设BD=x,则BC=x+15,
∴=,
解得:x=3,
∴在大于15米小于18米的范围内小丽看不见.
故答案为大于15米小于18米.
本题考查盲区及解直角三角形的知识,难度不大,关键是找出盲区.
16.3
【详解】
解:根据三视图可得长方体的长为4、宽为3、高为1,则左视图的面积=宽×高=3.
故答案为:3
17.22
【详解】
解:综合三视图,我们可以得出,这个几何模型的底层有3+1=4个小正方体,第二层有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是4+1=5个.
∴这个几何体的表面积是5×6-8=22,
故答案为22.
18.0<y≤2.5
【详解】
过D作DF⊥OC于F,交BE于H,OF=1.5,BH=0.5,
三角形DBH中,tan∠BDH=BH∶DH=0.5∶5,
因此三角形CDF中,CF=DF·tan∠BDH=1,
因此,OC=OF+CF=1+1.5=2.5.因此盲区的范围在0<y≤2.5.
19.26
【详解】
解:由主视图可知,搭成的几何体有三层,且有4列;由左视图可知,搭成的几何体共有3行;
第一层有7个正方体,第二层有2个正方体,第三层有1个正方体,
共有10个正方体,
∵搭在这个几何体的基础上添加相同大小的小正方体,以搭成一个大长方体,
∴搭成的大长方体的共有4×3×3=36个小正方体,
∴至少还需要36 10=26个小正方体.
故答案为:26.
20.见解析
【详解】
如图,小明的活动区域是A、B、C三个阴影部分区域.
21.见解析
【详解】
如图:连接AB、CD并延长交于点O,点O即为点光源,EG为旗杆的影子.
22.阴影部分A、B为亮亮活动的范围见解析.
【详解】
阴影部分A、B为亮亮活动的范围.
故答案为阴影部分A、B为亮亮活动的范围见解析.
23.见解析
【详解】
因为汽车司机的视线在车前车后有看不见的地方,即盲区.
汽车前进或倒退时,在车前或车后走很容易出危险.
24.①当圆柱底面圆的半径为1.5cm,高为4 cm时,表面积为:π (cm2),体积为:9π(cm3)
②当圆柱底面圆的半径为2cm,高为3 cm时,表面积为:20π(cm2),体积为:12π(cm3)
【详解】
∵一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为4 cm,3 cm的矩形,
∴①当圆柱底面圆的半径为1.5 cm,高为4 cm,
则圆柱的表面积为2π××4+2π=12π+π=π(cm2),
体积为π×4=9π(cm3);
②当圆柱底面圆的半径为2 cm,高为3 cm
则圆柱的表面积为2π×2×3+2π×22=12π+8π=20π(cm2),
体积为π×22×3=12π(cm3).
25.(1)见解析;(2)两个底面积: 6πcm2;侧面积: (9π+12)cm2;表面积:(15π+12)cm2.
【详解】
解:(1)左视图与主视图形状相同,有作垂线(直角)的痕迹(作法不唯一).
(2)两个底面积:2πr2×=6π(cm2);
侧面积:(2πr×+2r)×3=(3π+4)×3=9π+12(cm2);
表面积:15π+12(cm2).
26.(1) 楼房的高度约为15m;(2) 小猫不能晒到太阳.
【详解】
(1)当α=56.3°时,在Rt△ABE中, ∵tan56.3°=≈1.50,
∴AB=10 tan56.3°≈10×1.50=15(m),
即楼房的高度约为15米;
(2)当α=45°时,小猫不能再晒到太阳,理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD交于点P,此时的影长AP=AB≈15m,
设MN的延长线交AD于点H,
∵AC≈14.5m,NF=0.2m,
∴PH=AP﹣AC﹣CH≈15﹣14.5﹣0.2=0.3(m),
设直线MN与BP交于点Q,则HQ=PH=0.3m,
∴HQ=PH=0.3m,
∴点Q在MN上,
∴大楼的影子落在MN这个侧面上,
∴小猫不能晒到太阳.
答案第1页,共2页
答案第8页,共9页
九年级数学下册
一、单选题
1.下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是
A.(3)(1)(4)(2) B.(3)(2)(1)(4)
C.(3)(4)(1)(2) D.(2)(4)(1)(3)
2.发展工业是强国之梦的重要举措,如图所示零件的左视图是( )
A. B. C. D.
3.如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6 m的正方形.要使灯光能照射到整个舞台,则灯P的悬挂高度是( )
A.3m B.3m C.4m D.m
4.如图,太阳光线与地面成60°的角,照在地面的一只排球上,排球在地面的投影长是14,则排球的直径是( )
A.7 cm B.14 cm C.21 cm D.21cm
5.一个空心的圆柱如图所示,那么它的主视图是()
A. B. C. D.
6.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向上远移时,圆形阴影的大小的变化情况是( )
A.越来越小 B.越来越大 C.大小不变 D.不能确定
7.在下面的四个几何体中,它们各自的主视图与左视图可能相同的是( )
A. B. C. D.
8.如图是某几何体的三视图,下列判断正确的是( )
A.几何体是圆柱体,高为2 B.几何体是圆锥体,高为2
C.几何体是圆柱体,半径为2 D.几何体是圆锥体,直径为2
9.下列四个几何体的俯视图中与众不同的是( )
A. B. C. D.
10.如图所示,当小人向建筑物A靠近时,在建筑物B上形成的盲区( )
A.变大
B.变小
C.不变
D.无法确定
二、填空题
11.墙壁CD上D处有一盏灯(如图),小明站在A处测得他的影长与身长相等,都为1.6m,他向墙壁走1m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD=____.
12.如图,电影胶片上每一个图片的规格为3.5 cm×3.5 cm,放映屏幕的规格为2 m×2 m,若放映机的光源S距胶片20 cm,那么光源S距屏幕___米时,放映的图像刚好布满整个屏幕.
13.圆柱的主视图是长方形,左视图是________形,俯视图是________形.
14.从正面和左面看到长方体的图形如图所示(单位:cm),则从其上面看到图形的面积是_____ cm2.
15.如图,小丽站在30米高的楼顶远眺前方的广场,15米处有一个高为5米的障碍物,那么离楼房________的范围内小丽看不见.
16.长方体的主视图、俯视图如图,则其左视图面积为________.
17.如图是由若干个棱长为1的小正方体组合而成的一个几何体的三视图,则这个几何体的表面积是________.
主视图 左视图 俯视图
18.直角坐标系内,身高为1.5米的小强面向y轴站在x轴上的点A(-10,0)处,他的前方5米处有一堵墙,已知墙高2米,则站立的小强观察y(y>0)轴时,盲区(视力达不到的地方)范围是________.
19.如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要______个小立方块.
三、解答题
20.作图题: 如图所示:大王站在墙前,小明站在墙后,小明不能让大王看见,请你画出小明的活动区域.
21.已知小明和树的高与影长,试找出点光源和旗杆的影长.
22.明明与亮亮在借助两堵残墙玩捉迷藏游戏,若明明站在如图所示位置时,亮亮在哪个范围内活动是安全的?请在图(1)的俯视图(2)中画出亮亮的活动范围.
23.我们坐公共汽车下车后,不要从车前车后猛跑,为什么?
24.一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为4 cm,3 cm的矩形,求圆柱的表面积和体积.
25.一个圆柱体形零件,削去了占底面圆的四分之一部分的柱体(如图),现已画出了主视图与俯视图.
(1)请只用直尺和圆规,将此零件的左视图画在规定的位置(不必写作法,只须保留作图痕迹);
(2)若此零件底面圆的半径r=2cm,高h=3cm,求此零件的表面积.
26.如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin 56.3°≈0.83,cos 56.3°≈0.55,tan 56.3°≈1.5)
试卷第1页,共3页
参考答案:
1.C
【详解】
试题分析:根据从早晨到傍晚物体影子的指向是:西-西北-北-东北-东,影长由长变短,再变长,因此,
∵(1)为东北,(2)为东,(3)为西,(4)为西北,
∴将它们按时间先后顺序排列为(3)(4)(1)(2).
故选C.
2.D
【详解】
如图所示零件的左视图是.
故选D.
3.A
【详解】
连接AC,
∵∠APC=60°,
∴∠PAC=∠PCA=60°,
∵ABCD是边长为6m的正方形,
∴AC=6,OC=3
∴PC=6,
∴PO=3,
故选A.
4.C
【详解】
如图,点A与点B为太阳光线与球的切点,
则AB为排球的直径,CD=AB,cm,
在Rt△CDE中,sinE=
所以
即排球的直径为21cm.
故选C.
5.A
【详解】
根据主视图的定义,从前面看,得出图形是一个矩形(它里面含一个看不见的小矩形),即选项A的图形.
故选A.
6.A
【详解】
当点光源在物体上方,向下照射物体时,点光源离物体越近,影子越大,点光源离物体越远,影子越小.故圆形阴影越来越小.
故选A.
7.B
【详解】
A、此几何体主视图与左视图不相同,故此选项错误;
B、立方体的主视图与左视图都是矩形,故此选项正确;
B、三棱柱主视图是矩形,左视图也是矩形,矩形宽不相同,故此选项错误;
D、四棱柱的主视图是矩形,左视图也是矩形,矩形宽不相同,故此选项错误;
故选B.
8.A
【详解】
试题解析:根据主视图和左视图为矩形是柱体,根据俯视图是圆可判断出这个几何体应该是圆柱,
再根据左视图的高度得出圆柱体的高为2;
故选A.
9.B
【详解】
解:根据从上边看得到的图形是俯视图,可得
A的俯视图是第一列两个小正方形,第二列一个小正方形,
B的俯视图是第一列是两个小正方形,第二列是两个小正方形,
C的俯视图是第一列两个小正方形,第二列一个小正方形,
D的俯视图是第一列两个小正方形,第二列一个小正方形,
故选B.
10.A
【详解】
根据盲区即看不到的建筑物的高度.根据各物体的比例关系画出图形,数形结合,可以比较直观列出相关的比例关系式,从而得出答案.
解:如图所示:当小人向建筑物A靠近时,在建筑物B上形成的盲区不断增大,
故选A.
11.m
【详解】
如图:
根据题意得:BG=AF=AE=1.6m,AB=1m,
∵BG∥AF∥CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.6)m,AC=(x+1)m,
∴,
解得:x=, y=,
∴CD=m.
∴灯泡与地面的距离为米,
故答案为m.
12.
【详解】
运用位似图形的性质即可得;
设银幕距镜头xm,则有
,
解得:x=,
故答案为.
13.
【详解】
从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.
解:圆柱的主视图是长方形,左视图是长方形,俯视图是圆形.
本题考查了几何体的三视图的判断.
14.12
【详解】
根据从左面、从正面看到的形状图的相关数据可得:
从上面看到的形状图是长为4宽为3的长方形,
则从其上面看到图形的面积是4×3=12;
故答案为12.
15.15~18
【详解】
先判断出盲区,然后利用解直角三角形的知识求出盲区即可.
解:由题意得,盲区为BD,
设BD=x,则BC=x+15,
∴=,
解得:x=3,
∴在大于15米小于18米的范围内小丽看不见.
故答案为大于15米小于18米.
本题考查盲区及解直角三角形的知识,难度不大,关键是找出盲区.
16.3
【详解】
解:根据三视图可得长方体的长为4、宽为3、高为1,则左视图的面积=宽×高=3.
故答案为:3
17.22
【详解】
解:综合三视图,我们可以得出,这个几何模型的底层有3+1=4个小正方体,第二层有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是4+1=5个.
∴这个几何体的表面积是5×6-8=22,
故答案为22.
18.0<y≤2.5
【详解】
过D作DF⊥OC于F,交BE于H,OF=1.5,BH=0.5,
三角形DBH中,tan∠BDH=BH∶DH=0.5∶5,
因此三角形CDF中,CF=DF·tan∠BDH=1,
因此,OC=OF+CF=1+1.5=2.5.因此盲区的范围在0<y≤2.5.
19.26
【详解】
解:由主视图可知,搭成的几何体有三层,且有4列;由左视图可知,搭成的几何体共有3行;
第一层有7个正方体,第二层有2个正方体,第三层有1个正方体,
共有10个正方体,
∵搭在这个几何体的基础上添加相同大小的小正方体,以搭成一个大长方体,
∴搭成的大长方体的共有4×3×3=36个小正方体,
∴至少还需要36 10=26个小正方体.
故答案为:26.
20.见解析
【详解】
如图,小明的活动区域是A、B、C三个阴影部分区域.
21.见解析
【详解】
如图:连接AB、CD并延长交于点O,点O即为点光源,EG为旗杆的影子.
22.阴影部分A、B为亮亮活动的范围见解析.
【详解】
阴影部分A、B为亮亮活动的范围.
故答案为阴影部分A、B为亮亮活动的范围见解析.
23.见解析
【详解】
因为汽车司机的视线在车前车后有看不见的地方,即盲区.
汽车前进或倒退时,在车前或车后走很容易出危险.
24.①当圆柱底面圆的半径为1.5cm,高为4 cm时,表面积为:π (cm2),体积为:9π(cm3)
②当圆柱底面圆的半径为2cm,高为3 cm时,表面积为:20π(cm2),体积为:12π(cm3)
【详解】
∵一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为4 cm,3 cm的矩形,
∴①当圆柱底面圆的半径为1.5 cm,高为4 cm,
则圆柱的表面积为2π××4+2π=12π+π=π(cm2),
体积为π×4=9π(cm3);
②当圆柱底面圆的半径为2 cm,高为3 cm
则圆柱的表面积为2π×2×3+2π×22=12π+8π=20π(cm2),
体积为π×22×3=12π(cm3).
25.(1)见解析;(2)两个底面积: 6πcm2;侧面积: (9π+12)cm2;表面积:(15π+12)cm2.
【详解】
解:(1)左视图与主视图形状相同,有作垂线(直角)的痕迹(作法不唯一).
(2)两个底面积:2πr2×=6π(cm2);
侧面积:(2πr×+2r)×3=(3π+4)×3=9π+12(cm2);
表面积:15π+12(cm2).
26.(1) 楼房的高度约为15m;(2) 小猫不能晒到太阳.
【详解】
(1)当α=56.3°时,在Rt△ABE中, ∵tan56.3°=≈1.50,
∴AB=10 tan56.3°≈10×1.50=15(m),
即楼房的高度约为15米;
(2)当α=45°时,小猫不能再晒到太阳,理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD交于点P,此时的影长AP=AB≈15m,
设MN的延长线交AD于点H,
∵AC≈14.5m,NF=0.2m,
∴PH=AP﹣AC﹣CH≈15﹣14.5﹣0.2=0.3(m),
设直线MN与BP交于点Q,则HQ=PH=0.3m,
∴HQ=PH=0.3m,
∴点Q在MN上,
∴大楼的影子落在MN这个侧面上,
∴小猫不能晒到太阳.
答案第1页,共2页
答案第8页,共9页
