2021-2022学年人教版八年级数学下册第十八章平行四边形同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册第十八章平行四边形同步测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 270.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 17:00:19 | ||
图片预览




文档简介
第十八章平行四边形同步测试卷 2021-2022学年
人教版八年级数学下册
一、单选题
1.下列选项中,矩形具有的性质是( )
A.四边相等 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
2.在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A.OA=OC,OB=OD B.OA=OC,AB∥CD
C.AB=CD,OA=OC D.∠ADB=∠CBD,∠BAD=∠BCD
3.如图,在矩形中,对角线与相交于点,若,那么的度数是( )
A. B. C. D.
4.菱形的两条对角线长分别为6,8,则它的周长是( )
A.5 B.10 C.20 D.24
5.如图,菱形ABCD的周长为28,对角线AC,BD交于点O,E为AD的中点,则OE的长等于( )
A.2 B.3.5 C.7 D.14
6.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )
A. B. C. D.2
7.如图,在中,于点E,于点D;点F是AB的中点,连结DF,EF,设,,则
A. B. C. D.
8.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB,交AC于点E,则下列结论不正确的是( )
A.∠CAD=∠BAD B.BD=CD C.AE=ED D.DE=DB
9.如图,在□ABCD中,对角线 AC、BD 相交成的锐角α=30°,若 AC=8,BD=6,则□ABCD的面积是( )
A.6 B.8 C.10 D.12
10.如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )
A.2 B.3 C.4 D.5
二、填空题
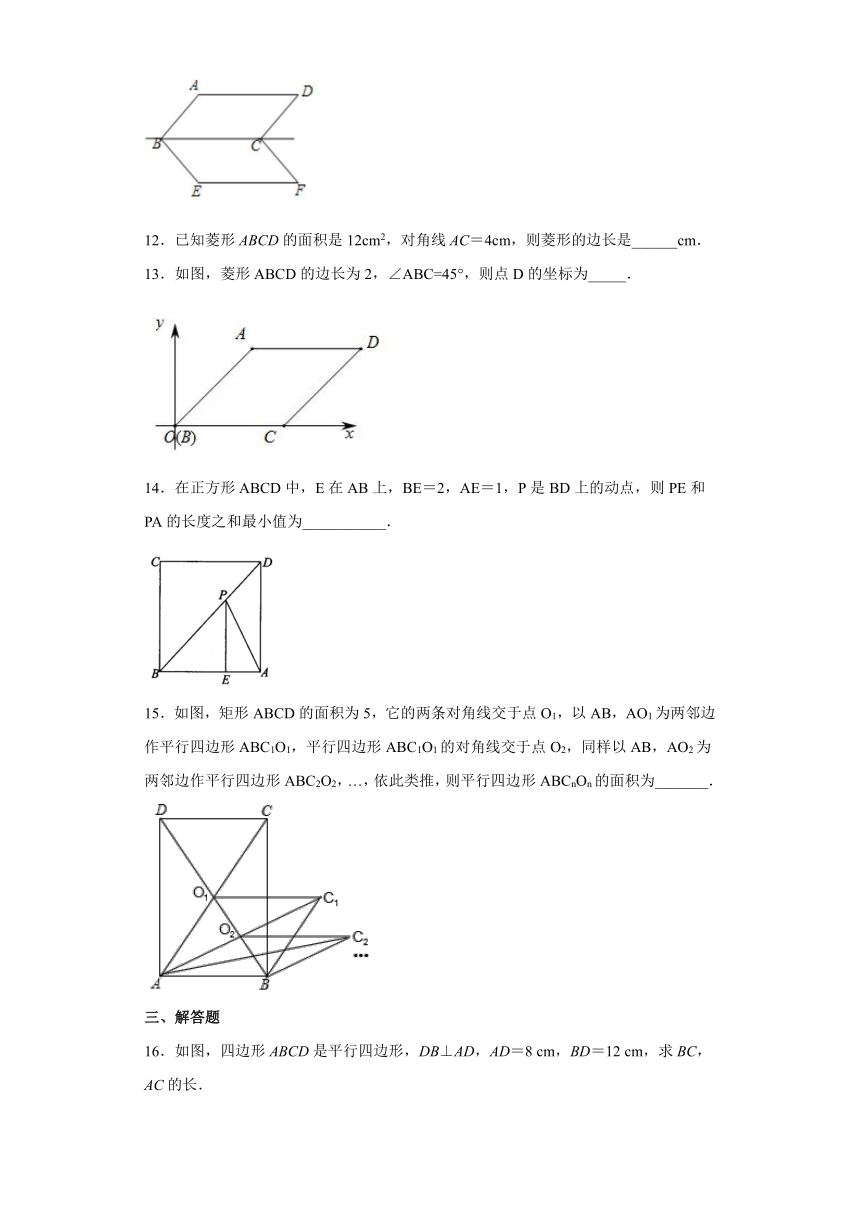
11.如图,若平行四边形ABCD与平行四边形EBCF关于BC所在直线对称,且∠ABE=90°,则∠F=_______°.
12.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是______cm.
13.如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为_____.
14.在正方形ABCD中,E在AB上,BE=2,AE=1,P是BD上的动点,则PE和PA的长度之和最小值为___________.
15.如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB,AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB,AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为_______.
三、解答题
16.如图,四边形ABCD是平行四边形,DB⊥AD,AD=8 cm,BD=12 cm,求BC,AC的长.
17.如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.
(1)求证:四边形BEDF是平行四边形;
(2)若AB=AD=8,BF=6,求AE的长.
18.如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=2,∠AEF=45°,求矩形ABCD的面积.
19.如图,将 ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD,求证:EC=DF.
20.已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
(1)求证:AF=DC;
(2)请问:AD与CF满足什么条件时,四边形AFDC是矩形,并说明理由.
21.如图,在 ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.
(1)求证:四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由.
试卷第1页,共3页
参考答案:
1.C
【详解】
A. 四边相等是菱形的性质,不是矩形的性质,故不符合题意;
B. 对角线互相垂直是菱形的性质,不是矩形的性质,故不符合题意;
C. 对角线相等是是矩形的性质,故符合题意;
D. 每条对角线平分一组对角是菱形的性质,不是矩形的性质,故不符合题意;
故选C.
2.C
【详解】
解:A.∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形),
∴A正确,故本选项不符合要求;
B. ∵AB∥CD
∴∠DAO=∠BCO,
在△DAO与△BCO中,
∴△DAO≌△BCO(ASA),
∴OD=OB,
又OA=OC,
∴四边形ABCD是平行四边形,∴B正确,故本选项不符合要求;
C. 由 AB=DC, OA=OC,
∴无法得出四边形ABCD是平行四边形.故不能能判定这个四边形是平行四边形,符合题意;∵AB∥DC,
D.∵∠ADB=∠CBD,∠BAD=∠BCD
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形),∴D正确,故本选项不符合要求;故选C.
3.D
【详解】
解:∵矩形ABCD中,对角线AC,BD相交于点O,
∴DB=AC,OD=OB,OA=OC,
∴OA=OD,
∴∠CAD=∠ADO,
∵∠COD=50°=∠CAD+∠ADO,
∴∠CAD=25°,
故选D.
4.C
【详解】
解:∵菱形的对角线互相垂直且平分,
∴勾股定理求出菱形的边长=5,
∴菱形的周长=20,
故选C.
5.B
【详解】
∵四边形ABCD为菱形,∴AB28=7,且O为BD的中点.
∵E为AD的中点,∴OE为△ABD的中位线,∴OEAB=3.5.
故选B.
6.B
【详解】
解:记AC与PQ的交点为O.
∵∠BAC=90°,AB=3,AC=4,
∴BC==5.
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∴PQ最短也就是PO最短.
过O作BC的垂线OP′.
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴,
∴OP′=,
∴则PQ的最小值为2OP′=,
故答案为.
7.B
【详解】
∵于点E,于点D;点F是AB的中点,
∴AF=DF,BF=EF,
∴∠ADF=∠DAF,∠EBF=∠BEF,
∵∠AFD+∠DFE=∠EBF+∠BEF=2∠EBF,∠BFE+∠DFE=∠DAF+∠ADF=2∠DAF,
∠AFD+∠DFE+∠BFE+∠DFE
=2∠EBF+2∠DAF
=2(∠EBF+∠DAF)
= 2(180°-∠C)
=360°-2∠C,
∴180°+∠DFE=360°-2∠C,
∴180°+x=360°-2y,
∴.
故选B.
8.D
【详解】
∵AB=AC,AD⊥BC,∴∠CAD=∠BAD,A正确,不符合题意;
BD=CD,B正确,不符合题意;
∵DE∥AB,∴∠EDA=∠BAD.
∵∠EAD=∠BAD,∴∠EAD=∠EDA,∴AE=ED,C正确,不符合题意;
DE与DB的关系不确定,D错误,符合题意.
故选D.
9.D
【详解】
如图,过点D作DE⊥AC于E点,设AC与BD相交于O点,
∵在平行四边形ABCD中,AC=8,BD=6,
∴DO=,
∵∠α=30°,DE⊥AC,
∴DE=,
∴△ACD的面积=,
∵四边形ABCD为平行四边形,
∴CD=AB,AD=BC,
在△ADC与△CBA中,
∵AD=CB,CD=AB,AC=CA,
∴△ADC △CBA(SSS),
∴△CBA的面积=△ADC的面积=6,
∴该平行四边形的面积=△CBA的面积+△ADC的面积=12,
故选:D.
10.C
【详解】
∵四边形ABCD是平行四边形,
∴BD=2BO,AD=BC,
∵BD=2AD,
∴BD=2BC,
∴BO=BC,
∵E为OC中点,
∴BE⊥AC,故①成立;
∵BE⊥AC,G是AB中点,
∴EG=AB,
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴EF=AB,
∴EF=EG,故②成立;
∵AB∥CD,EF∥CD,
∴EF∥AB,
∴∠FEG=∠BGE(两直线平行,内错角相等),
在△EFG和△GBE中,
∵BG=FE,∠FEG=∠BGE,GE=EG,
∴△EFG≌△GBE(SAS),即③成立;
∵BG=FE,EF∥AB,
∴四边形BEFG是平行四边形,
∵BE⊥AC,
∴GF⊥AC,
∵EF=EG,
∴∠AEG=∠AEF,
即EA平分∠GEF
故④正确,
若四边形BEFG是菱形
∴BE=BG=AB,
∴∠BAC=30°
与题意不符合
故⑤错误
故选C.
11.45°.
【详解】
解:根据题意,∠ABC=∠EBC=×90°=45°,
∵□EBCF ∴∠F=∠EBC=45°.
12.
【详解】
分析:根据菱形的面积公式求出另一对角线的长.然后因为菱形的对角线互相垂直平分,利用勾股定理求出菱形的边长.
详解:由菱形的面积公式,可得另一对角线长12×2÷4=6,
∵菱形的对角线互相垂直平分,
根据勾股定理可得菱形的边长=cm.
故答案为.
13.(, ).
【详解】
解:过点D作轴,垂足为E.
∵菱形的边长为2,∠ABC=45°,
∴CO=DC=2,∠DCE=45°,
在中,
∴点D坐标为
故答案为
14.
【详解】
解:连接AC,EC,EC与BD交于点P,此时PA+PE的最小,即PA+PE就是CE的长度
∵正方形ABCD中,BE=2,AE=1,
∴BC=AB=3,
∴CE= == ,
故答案为.
15.
【详解】
后面的每一个平行四边形都与第一个矩形ABCD同底不同高,而第n个平行四边形的高是矩形ABCD的,所以平行四边形ABCnOn的面积为.
16.BC=8 cm,AC=20 cm.
【详解】
解 ∵四边形ABCD是平行四边形,
∴BC=AD=8 cm,OA=OC,OB=OD=BD=6 cm,
∵BD⊥AD,
∴∠ADO=90°,
∴OA==10 cm,
∴AC=2OA=20 cm.
17.(1)见解析;(2).
【详解】
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCA,
在△ABF和△CDE中,,
∴△ABF≌△CDE(ASA),
∴BF=DE,∠AFB=∠CED,
∴BF∥DE,
∴四边形BEDF是平行四边形;
(2)连接BD交AC于G,如图所示:
∵AB=AD,
∴四边形ABCD是菱形,
∴AC⊥BD,
∴四边形BEDF是菱形,
∴BE=BF=6,EG=FG,
∵∠ABF=90°,AB=AD=8,BF=6,
∴AF==10,
∵△ABF的面积=AF·BG=AB×BF,
∴BG==,
∴EG==,
∴AE=AF-2EG=10-2×=.
18.(1)证明见解析;(2)8.
【详解】
试题分析:
(1)由矩形的性质得出∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,证出∠E=∠F,AE=CF,由ASA证明△CFP≌△AEQ,即可得出结论;(2)证明△BEP、△AEQ是等腰直角三角形,得出BE=BP=1,AQ=AE,求出PE= ,得出EQ=PE+PQ= ,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE-BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD的面积;
试题解析:
(1)证明:
∵四边形ABCD是矩形
∴∠A=∠ABC=∠C=∠ADC=90°
∴AB=CD,AD=BC,AB∥CD,AD∥BC
∴∠E=∠F
∵BE=DF
∴AE=CF
在△CFP和△AEQ中
∴△CFP≌△AEQ(ASA)
∴CP=AQ
(2)解:∵AD∥BC
∴∠PBE=∠A=90°
∵∠AEF=45°
∴△BEP、△AEQ是等腰直角三角形
∴BE=BP=1,AQ=AE
∴PE= BP=
∴EQ=PE+PQ=+2 =3
∴AQ=AE=3
∴AB=AE﹣BE=2
∵CP=AQ,AD=BC
∴DQ=BP=1
∴AD=AQ+DQ=3+1=4
∴矩形ABCD的面积=AB×AD=2×4=8.
19.见解析
【详解】
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵DE=AD,CF=BC,
∴DE=CF,
∵DE∥CF,
∴四边形DECF是平行四边形,
∴EC=DF.
20.(1)见解析;(2)见解析.
【详解】
(1)∵AF∥DC,
∴∠AFE=∠DCE,
又∵E为AD的中点,
∴AE=DE,
在△AEF和△DEC中,,
∴△AEF≌△DEC(AAS),
∴AF=DC;
(2)当AD=CF时,四边形AFDC是矩形;理由如下:
由(1)得:AF=DC且AF∥DC,
∴四边形AFDC是平行四边形,
又∵AD=CF,
∴四边形AFDC是矩形(对角线相等的平行四边形是矩形).
21.(1)见解析;(2)见解析.
【详解】
(1)∵四边形ABCD是平行四边形,
∴点O是AC的中点,
又∵点E是边AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
又∵点F在CB的延长线上,
∴OE∥BF,
∵EF∥BD,即EF∥OB,
∴四边形OBFE是平行四边形;
(2)当AD⊥BD时,四边形OBFE是矩形.
理由:由(1)可知,四边形OBFE是平行四边形,
又∵AD⊥BD,AD∥BC,且点F在BC的延长线上,
∴FC⊥BD,
∴∠OBF=90°,
∴四边形OBFE是矩形.
答案第1页,共2页
答案第10页,共11页
人教版八年级数学下册
一、单选题
1.下列选项中,矩形具有的性质是( )
A.四边相等 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
2.在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A.OA=OC,OB=OD B.OA=OC,AB∥CD
C.AB=CD,OA=OC D.∠ADB=∠CBD,∠BAD=∠BCD
3.如图,在矩形中,对角线与相交于点,若,那么的度数是( )
A. B. C. D.
4.菱形的两条对角线长分别为6,8,则它的周长是( )
A.5 B.10 C.20 D.24
5.如图,菱形ABCD的周长为28,对角线AC,BD交于点O,E为AD的中点,则OE的长等于( )
A.2 B.3.5 C.7 D.14
6.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )
A. B. C. D.2
7.如图,在中,于点E,于点D;点F是AB的中点,连结DF,EF,设,,则
A. B. C. D.
8.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB,交AC于点E,则下列结论不正确的是( )
A.∠CAD=∠BAD B.BD=CD C.AE=ED D.DE=DB
9.如图,在□ABCD中,对角线 AC、BD 相交成的锐角α=30°,若 AC=8,BD=6,则□ABCD的面积是( )
A.6 B.8 C.10 D.12
10.如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )
A.2 B.3 C.4 D.5
二、填空题
11.如图,若平行四边形ABCD与平行四边形EBCF关于BC所在直线对称,且∠ABE=90°,则∠F=_______°.
12.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是______cm.
13.如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为_____.
14.在正方形ABCD中,E在AB上,BE=2,AE=1,P是BD上的动点,则PE和PA的长度之和最小值为___________.
15.如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB,AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB,AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为_______.
三、解答题
16.如图,四边形ABCD是平行四边形,DB⊥AD,AD=8 cm,BD=12 cm,求BC,AC的长.
17.如图,ABCD是平行四边形,E、F是对角线AC上的两点,若∠ABF=∠CDE=90°.
(1)求证:四边形BEDF是平行四边形;
(2)若AB=AD=8,BF=6,求AE的长.
18.如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=2,∠AEF=45°,求矩形ABCD的面积.
19.如图,将 ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD,求证:EC=DF.
20.已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
(1)求证:AF=DC;
(2)请问:AD与CF满足什么条件时,四边形AFDC是矩形,并说明理由.
21.如图,在 ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.
(1)求证:四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由.
试卷第1页,共3页
参考答案:
1.C
【详解】
A. 四边相等是菱形的性质,不是矩形的性质,故不符合题意;
B. 对角线互相垂直是菱形的性质,不是矩形的性质,故不符合题意;
C. 对角线相等是是矩形的性质,故符合题意;
D. 每条对角线平分一组对角是菱形的性质,不是矩形的性质,故不符合题意;
故选C.
2.C
【详解】
解:A.∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形),
∴A正确,故本选项不符合要求;
B. ∵AB∥CD
∴∠DAO=∠BCO,
在△DAO与△BCO中,
∴△DAO≌△BCO(ASA),
∴OD=OB,
又OA=OC,
∴四边形ABCD是平行四边形,∴B正确,故本选项不符合要求;
C. 由 AB=DC, OA=OC,
∴无法得出四边形ABCD是平行四边形.故不能能判定这个四边形是平行四边形,符合题意;∵AB∥DC,
D.∵∠ADB=∠CBD,∠BAD=∠BCD
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形),∴D正确,故本选项不符合要求;故选C.
3.D
【详解】
解:∵矩形ABCD中,对角线AC,BD相交于点O,
∴DB=AC,OD=OB,OA=OC,
∴OA=OD,
∴∠CAD=∠ADO,
∵∠COD=50°=∠CAD+∠ADO,
∴∠CAD=25°,
故选D.
4.C
【详解】
解:∵菱形的对角线互相垂直且平分,
∴勾股定理求出菱形的边长=5,
∴菱形的周长=20,
故选C.
5.B
【详解】
∵四边形ABCD为菱形,∴AB28=7,且O为BD的中点.
∵E为AD的中点,∴OE为△ABD的中位线,∴OEAB=3.5.
故选B.
6.B
【详解】
解:记AC与PQ的交点为O.
∵∠BAC=90°,AB=3,AC=4,
∴BC==5.
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∴PQ最短也就是PO最短.
过O作BC的垂线OP′.
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴,
∴OP′=,
∴则PQ的最小值为2OP′=,
故答案为.
7.B
【详解】
∵于点E,于点D;点F是AB的中点,
∴AF=DF,BF=EF,
∴∠ADF=∠DAF,∠EBF=∠BEF,
∵∠AFD+∠DFE=∠EBF+∠BEF=2∠EBF,∠BFE+∠DFE=∠DAF+∠ADF=2∠DAF,
∠AFD+∠DFE+∠BFE+∠DFE
=2∠EBF+2∠DAF
=2(∠EBF+∠DAF)
= 2(180°-∠C)
=360°-2∠C,
∴180°+∠DFE=360°-2∠C,
∴180°+x=360°-2y,
∴.
故选B.
8.D
【详解】
∵AB=AC,AD⊥BC,∴∠CAD=∠BAD,A正确,不符合题意;
BD=CD,B正确,不符合题意;
∵DE∥AB,∴∠EDA=∠BAD.
∵∠EAD=∠BAD,∴∠EAD=∠EDA,∴AE=ED,C正确,不符合题意;
DE与DB的关系不确定,D错误,符合题意.
故选D.
9.D
【详解】
如图,过点D作DE⊥AC于E点,设AC与BD相交于O点,
∵在平行四边形ABCD中,AC=8,BD=6,
∴DO=,
∵∠α=30°,DE⊥AC,
∴DE=,
∴△ACD的面积=,
∵四边形ABCD为平行四边形,
∴CD=AB,AD=BC,
在△ADC与△CBA中,
∵AD=CB,CD=AB,AC=CA,
∴△ADC △CBA(SSS),
∴△CBA的面积=△ADC的面积=6,
∴该平行四边形的面积=△CBA的面积+△ADC的面积=12,
故选:D.
10.C
【详解】
∵四边形ABCD是平行四边形,
∴BD=2BO,AD=BC,
∵BD=2AD,
∴BD=2BC,
∴BO=BC,
∵E为OC中点,
∴BE⊥AC,故①成立;
∵BE⊥AC,G是AB中点,
∴EG=AB,
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴EF=AB,
∴EF=EG,故②成立;
∵AB∥CD,EF∥CD,
∴EF∥AB,
∴∠FEG=∠BGE(两直线平行,内错角相等),
在△EFG和△GBE中,
∵BG=FE,∠FEG=∠BGE,GE=EG,
∴△EFG≌△GBE(SAS),即③成立;
∵BG=FE,EF∥AB,
∴四边形BEFG是平行四边形,
∵BE⊥AC,
∴GF⊥AC,
∵EF=EG,
∴∠AEG=∠AEF,
即EA平分∠GEF
故④正确,
若四边形BEFG是菱形
∴BE=BG=AB,
∴∠BAC=30°
与题意不符合
故⑤错误
故选C.
11.45°.
【详解】
解:根据题意,∠ABC=∠EBC=×90°=45°,
∵□EBCF ∴∠F=∠EBC=45°.
12.
【详解】
分析:根据菱形的面积公式求出另一对角线的长.然后因为菱形的对角线互相垂直平分,利用勾股定理求出菱形的边长.
详解:由菱形的面积公式,可得另一对角线长12×2÷4=6,
∵菱形的对角线互相垂直平分,
根据勾股定理可得菱形的边长=cm.
故答案为.
13.(, ).
【详解】
解:过点D作轴,垂足为E.
∵菱形的边长为2,∠ABC=45°,
∴CO=DC=2,∠DCE=45°,
在中,
∴点D坐标为
故答案为
14.
【详解】
解:连接AC,EC,EC与BD交于点P,此时PA+PE的最小,即PA+PE就是CE的长度
∵正方形ABCD中,BE=2,AE=1,
∴BC=AB=3,
∴CE= == ,
故答案为.
15.
【详解】
后面的每一个平行四边形都与第一个矩形ABCD同底不同高,而第n个平行四边形的高是矩形ABCD的,所以平行四边形ABCnOn的面积为.
16.BC=8 cm,AC=20 cm.
【详解】
解 ∵四边形ABCD是平行四边形,
∴BC=AD=8 cm,OA=OC,OB=OD=BD=6 cm,
∵BD⊥AD,
∴∠ADO=90°,
∴OA==10 cm,
∴AC=2OA=20 cm.
17.(1)见解析;(2).
【详解】
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCA,
在△ABF和△CDE中,,
∴△ABF≌△CDE(ASA),
∴BF=DE,∠AFB=∠CED,
∴BF∥DE,
∴四边形BEDF是平行四边形;
(2)连接BD交AC于G,如图所示:
∵AB=AD,
∴四边形ABCD是菱形,
∴AC⊥BD,
∴四边形BEDF是菱形,
∴BE=BF=6,EG=FG,
∵∠ABF=90°,AB=AD=8,BF=6,
∴AF==10,
∵△ABF的面积=AF·BG=AB×BF,
∴BG==,
∴EG==,
∴AE=AF-2EG=10-2×=.
18.(1)证明见解析;(2)8.
【详解】
试题分析:
(1)由矩形的性质得出∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,证出∠E=∠F,AE=CF,由ASA证明△CFP≌△AEQ,即可得出结论;(2)证明△BEP、△AEQ是等腰直角三角形,得出BE=BP=1,AQ=AE,求出PE= ,得出EQ=PE+PQ= ,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE-BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD的面积;
试题解析:
(1)证明:
∵四边形ABCD是矩形
∴∠A=∠ABC=∠C=∠ADC=90°
∴AB=CD,AD=BC,AB∥CD,AD∥BC
∴∠E=∠F
∵BE=DF
∴AE=CF
在△CFP和△AEQ中
∴△CFP≌△AEQ(ASA)
∴CP=AQ
(2)解:∵AD∥BC
∴∠PBE=∠A=90°
∵∠AEF=45°
∴△BEP、△AEQ是等腰直角三角形
∴BE=BP=1,AQ=AE
∴PE= BP=
∴EQ=PE+PQ=+2 =3
∴AQ=AE=3
∴AB=AE﹣BE=2
∵CP=AQ,AD=BC
∴DQ=BP=1
∴AD=AQ+DQ=3+1=4
∴矩形ABCD的面积=AB×AD=2×4=8.
19.见解析
【详解】
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵DE=AD,CF=BC,
∴DE=CF,
∵DE∥CF,
∴四边形DECF是平行四边形,
∴EC=DF.
20.(1)见解析;(2)见解析.
【详解】
(1)∵AF∥DC,
∴∠AFE=∠DCE,
又∵E为AD的中点,
∴AE=DE,
在△AEF和△DEC中,,
∴△AEF≌△DEC(AAS),
∴AF=DC;
(2)当AD=CF时,四边形AFDC是矩形;理由如下:
由(1)得:AF=DC且AF∥DC,
∴四边形AFDC是平行四边形,
又∵AD=CF,
∴四边形AFDC是矩形(对角线相等的平行四边形是矩形).
21.(1)见解析;(2)见解析.
【详解】
(1)∵四边形ABCD是平行四边形,
∴点O是AC的中点,
又∵点E是边AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
又∵点F在CB的延长线上,
∴OE∥BF,
∵EF∥BD,即EF∥OB,
∴四边形OBFE是平行四边形;
(2)当AD⊥BD时,四边形OBFE是矩形.
理由:由(1)可知,四边形OBFE是平行四边形,
又∵AD⊥BD,AD∥BC,且点F在BC的延长线上,
∴FC⊥BD,
∴∠OBF=90°,
∴四边形OBFE是矩形.
答案第1页,共2页
答案第10页,共11页
