2021-2022学年人教版数学七年级下册6.1.1 算术平方根 课件(19张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册6.1.1 算术平方根 课件(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 30.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 19:24:42 | ||
图片预览





文档简介
(共19张PPT)
6.1.1 算术平方根
情境引入
问题 学校要举行美术作品比赛,小鸥想裁出一块边长为2 dm 的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的面积长应取多少
请你说一说解决问题的思路.
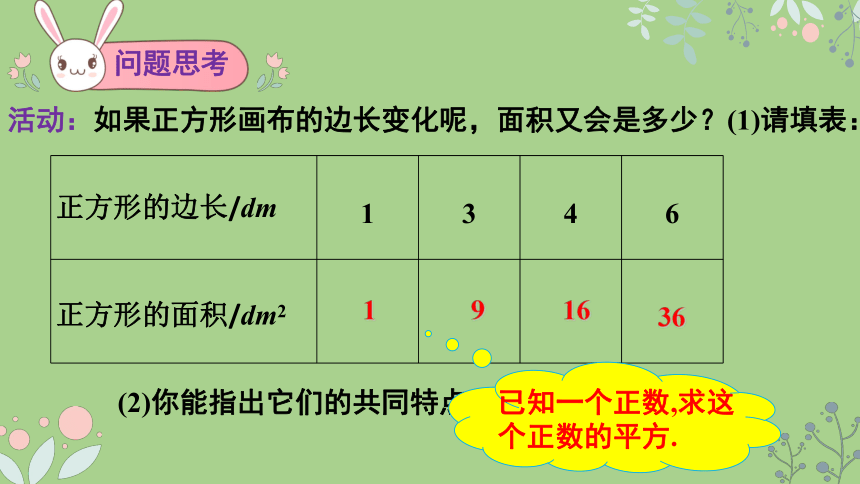
问题思考
活动:如果正方形画布的边长变化呢,面积又会是多少?(1)请填表:
正方形的边长/dm 1 3 4 6
正方形的面积/dm2
(2)你能指出它们的共同特点吗?
已知一个正数,求这个正数的平方.
1
9
16
36
情境引入
问题 学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm 的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少
请你说一说解决问题的思路.
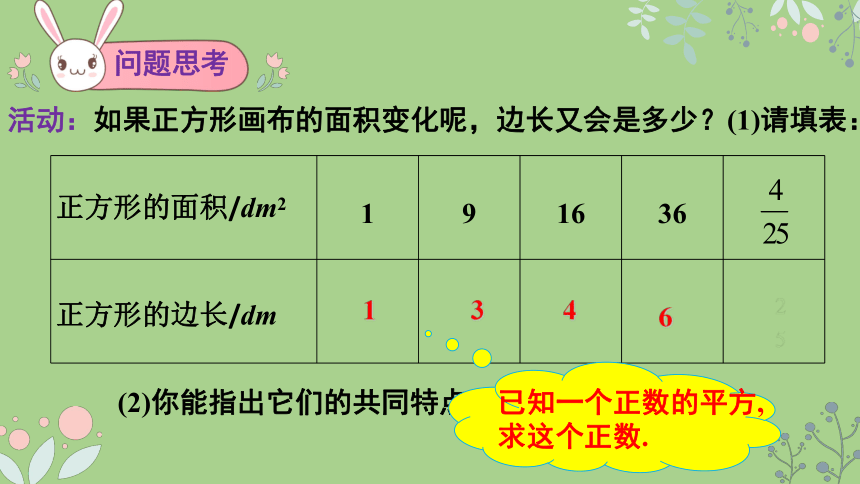
问题思考
活动:如果正方形画布的面积变化呢,边长又会是多少?(1)请填表:
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
(2)你能指出它们的共同特点吗?
已知一个正数的平方,求这个正数.
1
3
4
6
总结性质
算术平方根
1.定义:一般地,如果一个正数x的平方等于a,即x2=a,
那么这个正数x叫做a的算术平方根.
3.算术平方根的表示方法:
a 的算术平方根记为 ,读作“根号a”,a叫做被开方数.
2.规定:0的算术平方根是0
(a≥0)
基础小练
1.因为22=4 ,所以4的算术平方根是__;
因为__2=9 ,所以9的算术平方根是__;
因为42=__ ,所以__的算术平方根是__;
因为__2=__ ,所以__的算术平方根是__;
2.下列说法正确的是 .
①5是25的算术平方根.②0.01是0.1的算术平方根.③0的算术平方根是0.④-0.01的算术平方根是0.1.⑤ - 5是25的算术平方根.
2
3
3
16
4
16
①
③
性质总结
1.只有非负数有算数平方根
3.算数平方根没有负数
2.负数没有算数平方根
性质总结
a的算术平方根
互为逆运算
平方根号
被开方数
读作:根号a
(a≥0)
怎么用符号来表示一个数的算术平方根?
(x≥0)
如果x2=a(x≥0), 那么x =
典例分析
例 求下列各数的算术平方根:
(1) 100 (2) (3)0.0001
归纳:被开方数越大,对应的算术平方根也越大.
算术平方根非负性的应用
以前学的非负性:
平方具有非负性,即
绝对值具有非负性,即
算术平方根具有双重非负性:
相关练习
参考答案
知识层面总结
思想方法
总结
感谢聆听
6.1.1 算术平方根
情境引入
问题 学校要举行美术作品比赛,小鸥想裁出一块边长为2 dm 的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的面积长应取多少
请你说一说解决问题的思路.
问题思考
活动:如果正方形画布的边长变化呢,面积又会是多少?(1)请填表:
正方形的边长/dm 1 3 4 6
正方形的面积/dm2
(2)你能指出它们的共同特点吗?
已知一个正数,求这个正数的平方.
1
9
16
36
情境引入
问题 学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm 的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少
请你说一说解决问题的思路.
问题思考
活动:如果正方形画布的面积变化呢,边长又会是多少?(1)请填表:
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
(2)你能指出它们的共同特点吗?
已知一个正数的平方,求这个正数.
1
3
4
6
总结性质
算术平方根
1.定义:一般地,如果一个正数x的平方等于a,即x2=a,
那么这个正数x叫做a的算术平方根.
3.算术平方根的表示方法:
a 的算术平方根记为 ,读作“根号a”,a叫做被开方数.
2.规定:0的算术平方根是0
(a≥0)
基础小练
1.因为22=4 ,所以4的算术平方根是__;
因为__2=9 ,所以9的算术平方根是__;
因为42=__ ,所以__的算术平方根是__;
因为__2=__ ,所以__的算术平方根是__;
2.下列说法正确的是 .
①5是25的算术平方根.②0.01是0.1的算术平方根.③0的算术平方根是0.④-0.01的算术平方根是0.1.⑤ - 5是25的算术平方根.
2
3
3
16
4
16
①
③
性质总结
1.只有非负数有算数平方根
3.算数平方根没有负数
2.负数没有算数平方根
性质总结
a的算术平方根
互为逆运算
平方根号
被开方数
读作:根号a
(a≥0)
怎么用符号来表示一个数的算术平方根?
(x≥0)
如果x2=a(x≥0), 那么x =
典例分析
例 求下列各数的算术平方根:
(1) 100 (2) (3)0.0001
归纳:被开方数越大,对应的算术平方根也越大.
算术平方根非负性的应用
以前学的非负性:
平方具有非负性,即
绝对值具有非负性,即
算术平方根具有双重非负性:
相关练习
参考答案
知识层面总结
思想方法
总结
感谢聆听
