浙教版(2020)信息技术八年级上册 第8课循环结构——for循环课件(23张PPT)
文档属性
| 名称 | 浙教版(2020)信息技术八年级上册 第8课循环结构——for循环课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-03-16 22:57:38 | ||
图片预览





文档简介
(共18张PPT)
2021浙江教育出版社八(上)
第9课 for循环的应用实例
《哈佛家训》——国王和麦粒的故事古代印度的舍罕王,打算重赏国际象棋的发明者——宰相西萨。西萨向国王请求说:“陛下,我想向您要一点粮食,然后将它们分给贫困的百姓。”国王高兴地同意了。“请您派人在这张棋盘的第一个小格内放上一粒麦子,在第二格放两粒,第三格放四粒·····照这样下去,每一格内的数量比前一格增加一倍。陛下啊,把这些摆满棋盘上所有64格的麦粒都赏赐给您的仆人吧!我只要这些就够了。”国王许诺了宰相这个看起来微不足道的请求。但是当人们把一袋一袋麦子搬来开始计数才发现,就算把全国甚至全世界的麦粒都拿来,也满足不了他的要求。那么,这位大臣要求得到的麦粒到底是多少呢?1
问题分析
存放模型
2
算法设计
流程图分析
3
编写代码
计数器和累加器
4
调试运行
观察结果
CONTENT
棋盘上麦粒的存放模型
问题分析
1
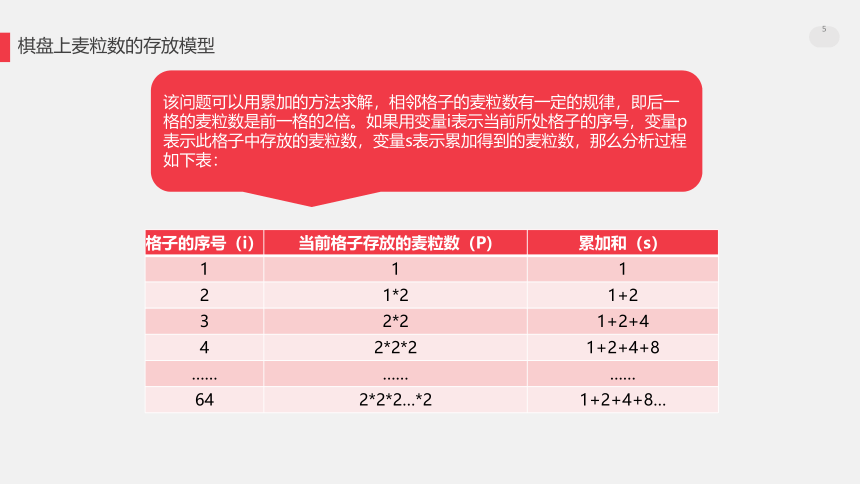
棋盘上麦粒数的存放模型格子的序号(i)当前格子存放的麦粒数(P)累加和(s)11121*21+232*21+2+442*2*21+2+4+8………………642*2*2…*21+2+4+8…该问题可以用累加的方法求解,相邻格子的麦粒数有一定的规律,即后一格的麦粒数是前一格的2倍。如果用变量i表示当前所处格子的序号,变量p表示此格子中存放的麦粒数,变量s表示累加得到的麦粒数,那么分析过程如下表:流程图
算法分析
2
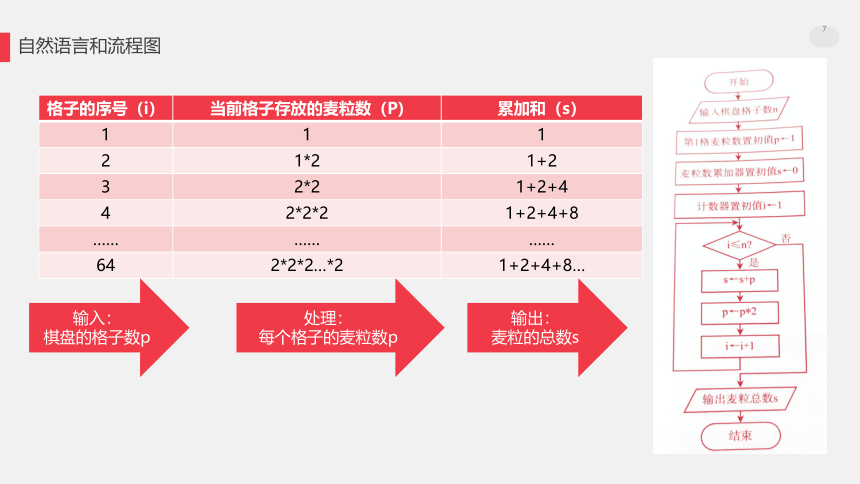
自然语言和流程图格子的序号(i)当前格子存放的麦粒数(P)累加和(s)11121*21+232*21+2+442*2*21+2+4+8………………642*2*2…*21+2+4+8…输入:棋盘的格子数p处理:每个格子的麦粒数p输出:麦粒的总数s计数器和累加器
编写代码
3
程序代码# n表示棋盘的格子数n=int(input("请输入棋盘格子数"))p=1 #第1格麦粒p置初值1s=0 #累加器s初始化为0#通过for语句循环累加,并输出麦粒总数for i in range(1,n+1):s=s+pp=p*2print("棋盘格子数为",n",麦粒总数:",s)根据设计的算法,先输入棋盘的格子数n,然后通过for循环语句实现累加。麦粒总数s需要在循环之前进行数值初始化为0,第1格麦粒数p数值初始化为1.循环的边界条件,也就是考虑循环的进入和退出条件。本例中,循环是从第1格到第64格,因为包含第64个格子本身,所以函数range() 的终值为n+1.知识链接:计数器知识链接:累加器在算法执行过程中,用来记录某件事件发生次数的变量。1.计数器的初始值通常置为0.2.循环体中的计数语句格式通常为i=i+1在算法的执行过程汇中,用来生成并存储数据累加和的变量。1.累加器的初始值通常置为0.2.循环体中的累加语句通常为s=s+x观察结果
调试运行
4
调试运行# n表示棋盘的格子数n=int(input("请输入棋盘格子数"))p=1 #第1格麦粒p置初值1s=0 #累加器s初始化为0#通过for语句循环累加,并输出每个格子的麦粒数#最后输出麦粒总重量,单位换算成吨for i in range(1,n+1):s=s+pp=p*2print("当前格子序号为",i",当前格子麦粒数:",int(p/2))s=(s*0.03)/(1000*1000)print("麦粒总重量(吨)",format(s,'.2f'))“F5”,输入棋盘数,观察运行结果。为了更好呈现麦粒重量和计算过程,可以将麦粒数转为吨数,按照每粒约003克计算,并在循环过程中输出每个格子的麦粒数。随便练习:程序填空运行结果随堂练习和迁移寻找“水仙花”数。水仙花数是指一个三位数,它的每个数位上的数的3次幂之和 等于它本身。例如:153是水仙花数。因为13+53+33=153.在如下程序的划线处填空。随堂练习和迁移lst=[] #初置空列表for <填空>a=i%10 #个位b=(i//10)%10 #十位c=i//100 #百位if(a**3+b**3+c**3)==i:lst.append(i)print(lst)For循环语句的格式和执行流程01For循环的程序设计.03程序中的累加器02第九课for循环的应用实例通过“国家象棋棋盘盘上麦粒问题”程序实例,理解for循环的语句格式和执行流程,理解程序中累加器的作用,能够编写比较复杂的for循环程序。感悟与体验千百年后的今天,我们都知道事情的结局:国王无法实现自己的承诺。这是一个长达20位的天文数字!这样多的麦粒相当于全世界两千年的产量。不过当时所有在场的人都不知道这个结果。他们眼看着仅用一小碗麦粒就填满了棋盘上十几个方格,禁不住笑了起来,连国王也认为西萨太傻了。 弱小的事物当初总是被人讥笑,但只要不断积聚力量,就会逐渐强大。从弱变强的过程可能是难以察觉的,当你能够看见时,它就一定强大的令人难以置信。
2021浙江教育出版社八(上)
第9课 for循环的应用实例
《哈佛家训》——国王和麦粒的故事古代印度的舍罕王,打算重赏国际象棋的发明者——宰相西萨。西萨向国王请求说:“陛下,我想向您要一点粮食,然后将它们分给贫困的百姓。”国王高兴地同意了。“请您派人在这张棋盘的第一个小格内放上一粒麦子,在第二格放两粒,第三格放四粒·····照这样下去,每一格内的数量比前一格增加一倍。陛下啊,把这些摆满棋盘上所有64格的麦粒都赏赐给您的仆人吧!我只要这些就够了。”国王许诺了宰相这个看起来微不足道的请求。但是当人们把一袋一袋麦子搬来开始计数才发现,就算把全国甚至全世界的麦粒都拿来,也满足不了他的要求。那么,这位大臣要求得到的麦粒到底是多少呢?1
问题分析
存放模型
2
算法设计
流程图分析
3
编写代码
计数器和累加器
4
调试运行
观察结果
CONTENT
棋盘上麦粒的存放模型
问题分析
1
棋盘上麦粒数的存放模型格子的序号(i)当前格子存放的麦粒数(P)累加和(s)11121*21+232*21+2+442*2*21+2+4+8………………642*2*2…*21+2+4+8…该问题可以用累加的方法求解,相邻格子的麦粒数有一定的规律,即后一格的麦粒数是前一格的2倍。如果用变量i表示当前所处格子的序号,变量p表示此格子中存放的麦粒数,变量s表示累加得到的麦粒数,那么分析过程如下表:流程图
算法分析
2
自然语言和流程图格子的序号(i)当前格子存放的麦粒数(P)累加和(s)11121*21+232*21+2+442*2*21+2+4+8………………642*2*2…*21+2+4+8…输入:棋盘的格子数p处理:每个格子的麦粒数p输出:麦粒的总数s计数器和累加器
编写代码
3
程序代码# n表示棋盘的格子数n=int(input("请输入棋盘格子数"))p=1 #第1格麦粒p置初值1s=0 #累加器s初始化为0#通过for语句循环累加,并输出麦粒总数for i in range(1,n+1):s=s+pp=p*2print("棋盘格子数为",n",麦粒总数:",s)根据设计的算法,先输入棋盘的格子数n,然后通过for循环语句实现累加。麦粒总数s需要在循环之前进行数值初始化为0,第1格麦粒数p数值初始化为1.循环的边界条件,也就是考虑循环的进入和退出条件。本例中,循环是从第1格到第64格,因为包含第64个格子本身,所以函数range() 的终值为n+1.知识链接:计数器知识链接:累加器在算法执行过程中,用来记录某件事件发生次数的变量。1.计数器的初始值通常置为0.2.循环体中的计数语句格式通常为i=i+1在算法的执行过程汇中,用来生成并存储数据累加和的变量。1.累加器的初始值通常置为0.2.循环体中的累加语句通常为s=s+x观察结果
调试运行
4
调试运行# n表示棋盘的格子数n=int(input("请输入棋盘格子数"))p=1 #第1格麦粒p置初值1s=0 #累加器s初始化为0#通过for语句循环累加,并输出每个格子的麦粒数#最后输出麦粒总重量,单位换算成吨for i in range(1,n+1):s=s+pp=p*2print("当前格子序号为",i",当前格子麦粒数:",int(p/2))s=(s*0.03)/(1000*1000)print("麦粒总重量(吨)",format(s,'.2f'))“F5”,输入棋盘数,观察运行结果。为了更好呈现麦粒重量和计算过程,可以将麦粒数转为吨数,按照每粒约003克计算,并在循环过程中输出每个格子的麦粒数。随便练习:程序填空运行结果随堂练习和迁移寻找“水仙花”数。水仙花数是指一个三位数,它的每个数位上的数的3次幂之和 等于它本身。例如:153是水仙花数。因为13+53+33=153.在如下程序的划线处填空。随堂练习和迁移lst=[] #初置空列表for <填空>a=i%10 #个位b=(i//10)%10 #十位c=i//100 #百位if(a**3+b**3+c**3)==i:lst.append(i)print(lst)For循环语句的格式和执行流程01For循环的程序设计.03程序中的累加器02第九课for循环的应用实例通过“国家象棋棋盘盘上麦粒问题”程序实例,理解for循环的语句格式和执行流程,理解程序中累加器的作用,能够编写比较复杂的for循环程序。感悟与体验千百年后的今天,我们都知道事情的结局:国王无法实现自己的承诺。这是一个长达20位的天文数字!这样多的麦粒相当于全世界两千年的产量。不过当时所有在场的人都不知道这个结果。他们眼看着仅用一小碗麦粒就填满了棋盘上十几个方格,禁不住笑了起来,连国王也认为西萨太傻了。 弱小的事物当初总是被人讥笑,但只要不断积聚力量,就会逐渐强大。从弱变强的过程可能是难以察觉的,当你能够看见时,它就一定强大的令人难以置信。
