4.3.3 余角和补角
图片预览


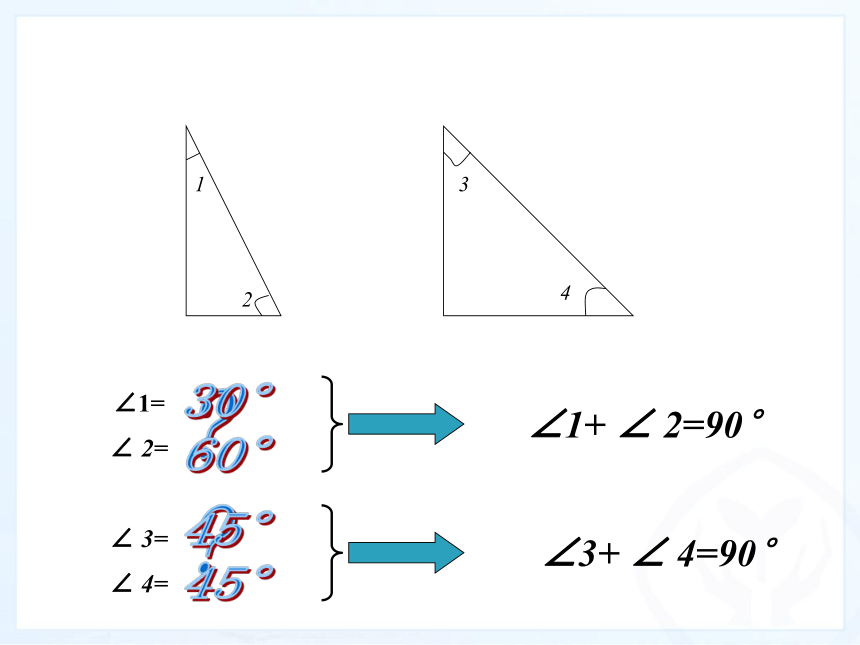




文档简介
课件24张PPT。4.3 角(第5课时)
4.3.3 余角和补角大家拿出手中的一副三角板! 这一副三角板的各个角的角度分别是多少度呢? 每块三角板中都有一个角是90°,而另外两个角是30°、60°、45°、45°非直角的两个角有什么关系?∠1=
∠ 2=
∠ 3=
∠ 4=?
?30°
60°45°
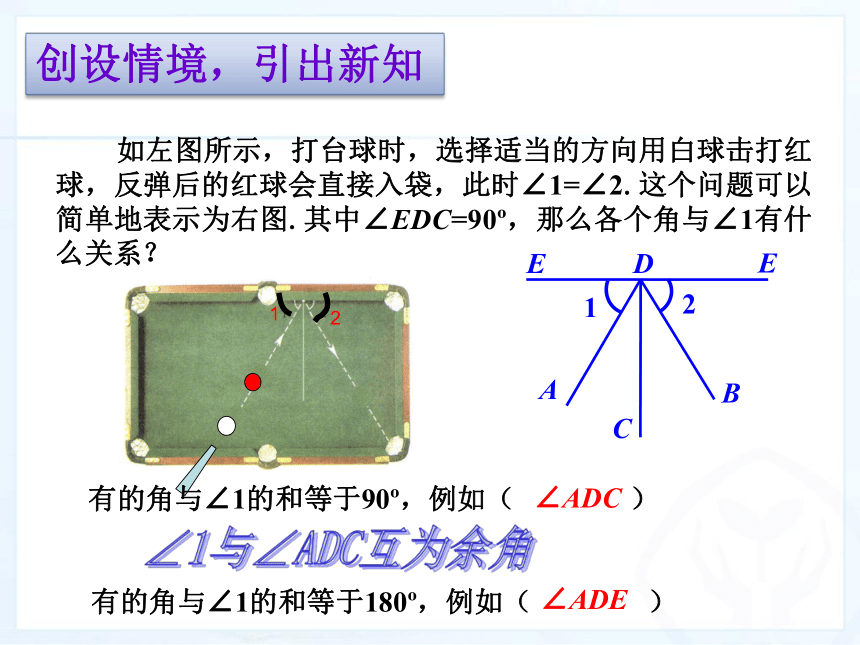
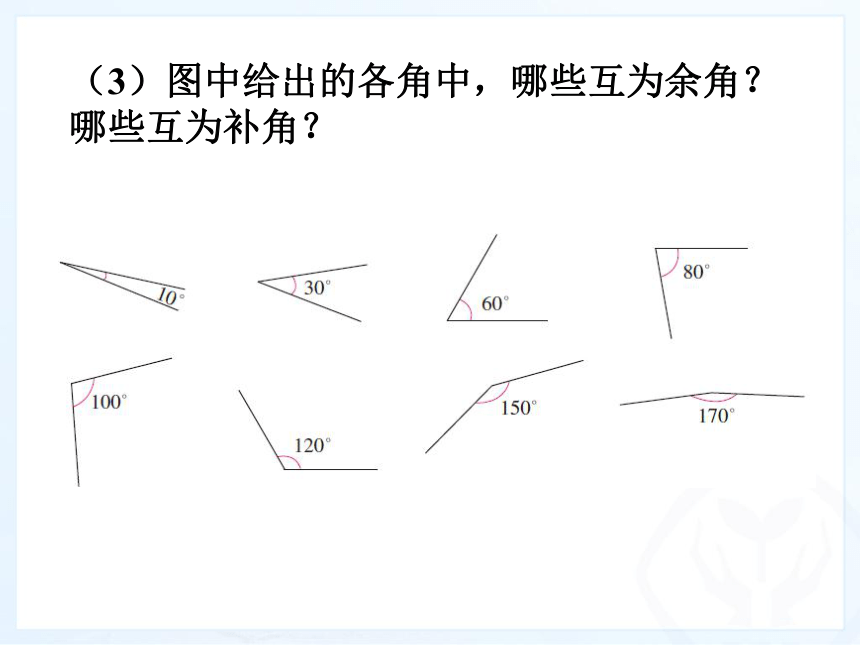
45°∠1+ ∠ 2=90°∠3+ ∠ 4=90° 如果两个角的和等于90o(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.创设情境,引出新知创设情境,引出新知 有的角与∠1的和等于90o,例如( ) ∠ADC 有的角与∠1的和等于180o,例如( ) ∠ADE∠1与∠ADC互为余角创设情境,引出新知 如果两个角的和等于180o(平角),就说这两个角互为补角,即其中一个角是另一个角的补角. 1.定义中的“互为”是什么意思? 2.把下图中∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?理解定义,巩固运用即每一个角都是另一个角的余角(补角) 两角互余,两角互补只是两个角间的数量关系,而与两角的位置无关。理解定义,巩固运用(1)若∠1与∠2互补,则∠1+∠2=______. (2) ∠1=90o-∠2,则∠1与∠2的关系为___________.180°互为余角(3)图中给出的各角中,哪些互为余角?哪些互为补角? (1)已知∠1与∠2,∠3都互为补角.那么∠2和∠3的大小有什么关系?推导性质,理解运用 由∠1与∠2和∠3都互为补角,
那么 ∠2=180o-∠1,
∠3=180o-∠1,所以∠2=∠3.
(2)已知∠1与∠2互补,∠3与∠4互补.若∠1=∠3,那么∠2和∠4 相等吗?为什么? 由∠1与∠2互补,得∠1+∠2=180o,
所以 ∠2=180o-∠1. 由∠3与∠4互补,得∠3+∠4=180o, 所以∠4=180o-∠3.又因为∠1=∠3,180o-∠1=180o-∠3,所以∠2=∠4.推导性质,理解运用 如果∠1与∠2互余, ∠3与∠4互余,并且∠1= ∠3,那么∠2与∠4相等吗?为什么? 由∠1与∠2互余,得∠1+∠2=90°,
所以 ∠2=90o-∠1. 由∠3与∠4互余,得∠3+∠4=90o, 所以∠4=90o-∠3.又因为∠1=∠3,90o-∠1=90o-∠3,所以∠2=∠4.等角 的余角相等.等角 的补角相等.对于余角是否也有类似性质?(同角)(同角)同角的余角相等等角的补角相等∠1∠3∠4∠5推导性质,理解运用推导性质,理解运用推导性质,理解运用所以∠COD +∠COE= ∠AOC+ ∠BOC 解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.又因为射线OD和射线OE分别平分∠AOC∠BOC,= (∠AOC+ ∠BOC)=90°所以, ∠COD 和∠COE互为余角,同理, ∠AOD 和∠BOE,
∠AOD 和∠COE ,
∠COD 和∠BOE也互为余角. 有时以正北、正南方向为基准,描述物体运动的方向. 表示方向的角(方位角)在航行、测绘等工作中经常用到.推导性质,理解运用上北下南左西右东例 如图,货轮O在航行过程中,发现灯塔A在它南偏东60o的方向上,同时,在它北偏东40o、南偏西10o、西北(即北偏西45o)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.● A40° B C10°45° D推导性质,理解运用强化练习,巩固提高它的余角是90o-70o39′=19o21′,
它的补角是180o-70o39′=109o21′.由180o- ∠α=3 ∠α,解得∠α=45o.锐角(4)已知一个角的补角是这个角的余角的3倍,求这个角。课堂小结,自我完善∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等.同角或等角的补角相等.拓展延伸,布置作业 1.课本第141页第13题.
2.∠α的余角是它的3倍,∠α是多少度? 3.(选做题)一个角的余角比这个角的补角的 还小10°,求这个角的余角及这个角的补角的度数.下节课我们继续学习!再见 问题1: 如图,在木箱顶点B处有一个食物,顶点A处的小蚂蚁想去吃掉食物,问沿着木箱表面最近的路线如何走?这样的线路有多少条? A B “蚂蚁吃食物”的问题
4.3.3 余角和补角大家拿出手中的一副三角板! 这一副三角板的各个角的角度分别是多少度呢? 每块三角板中都有一个角是90°,而另外两个角是30°、60°、45°、45°非直角的两个角有什么关系?∠1=
∠ 2=
∠ 3=
∠ 4=?
?30°
60°45°
45°∠1+ ∠ 2=90°∠3+ ∠ 4=90° 如果两个角的和等于90o(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.创设情境,引出新知创设情境,引出新知 有的角与∠1的和等于90o,例如( ) ∠ADC 有的角与∠1的和等于180o,例如( ) ∠ADE∠1与∠ADC互为余角创设情境,引出新知 如果两个角的和等于180o(平角),就说这两个角互为补角,即其中一个角是另一个角的补角. 1.定义中的“互为”是什么意思? 2.把下图中∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?理解定义,巩固运用即每一个角都是另一个角的余角(补角) 两角互余,两角互补只是两个角间的数量关系,而与两角的位置无关。理解定义,巩固运用(1)若∠1与∠2互补,则∠1+∠2=______. (2) ∠1=90o-∠2,则∠1与∠2的关系为___________.180°互为余角(3)图中给出的各角中,哪些互为余角?哪些互为补角? (1)已知∠1与∠2,∠3都互为补角.那么∠2和∠3的大小有什么关系?推导性质,理解运用 由∠1与∠2和∠3都互为补角,
那么 ∠2=180o-∠1,
∠3=180o-∠1,所以∠2=∠3.
(2)已知∠1与∠2互补,∠3与∠4互补.若∠1=∠3,那么∠2和∠4 相等吗?为什么? 由∠1与∠2互补,得∠1+∠2=180o,
所以 ∠2=180o-∠1. 由∠3与∠4互补,得∠3+∠4=180o, 所以∠4=180o-∠3.又因为∠1=∠3,180o-∠1=180o-∠3,所以∠2=∠4.推导性质,理解运用 如果∠1与∠2互余, ∠3与∠4互余,并且∠1= ∠3,那么∠2与∠4相等吗?为什么? 由∠1与∠2互余,得∠1+∠2=90°,
所以 ∠2=90o-∠1. 由∠3与∠4互余,得∠3+∠4=90o, 所以∠4=90o-∠3.又因为∠1=∠3,90o-∠1=90o-∠3,所以∠2=∠4.等角 的余角相等.等角 的补角相等.对于余角是否也有类似性质?(同角)(同角)同角的余角相等等角的补角相等∠1∠3∠4∠5推导性质,理解运用推导性质,理解运用推导性质,理解运用所以∠COD +∠COE= ∠AOC+ ∠BOC 解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.又因为射线OD和射线OE分别平分∠AOC∠BOC,= (∠AOC+ ∠BOC)=90°所以, ∠COD 和∠COE互为余角,同理, ∠AOD 和∠BOE,
∠AOD 和∠COE ,
∠COD 和∠BOE也互为余角. 有时以正北、正南方向为基准,描述物体运动的方向. 表示方向的角(方位角)在航行、测绘等工作中经常用到.推导性质,理解运用上北下南左西右东例 如图,货轮O在航行过程中,发现灯塔A在它南偏东60o的方向上,同时,在它北偏东40o、南偏西10o、西北(即北偏西45o)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.● A40° B C10°45° D推导性质,理解运用强化练习,巩固提高它的余角是90o-70o39′=19o21′,
它的补角是180o-70o39′=109o21′.由180o- ∠α=3 ∠α,解得∠α=45o.锐角(4)已知一个角的补角是这个角的余角的3倍,求这个角。课堂小结,自我完善∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等.同角或等角的补角相等.拓展延伸,布置作业 1.课本第141页第13题.
2.∠α的余角是它的3倍,∠α是多少度? 3.(选做题)一个角的余角比这个角的补角的 还小10°,求这个角的余角及这个角的补角的度数.下节课我们继续学习!再见 问题1: 如图,在木箱顶点B处有一个食物,顶点A处的小蚂蚁想去吃掉食物,问沿着木箱表面最近的路线如何走?这样的线路有多少条? A B “蚂蚁吃食物”的问题
