2021—2022学年人教版数学八年级下册18.1.2平行四边形的判定巩固练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册18.1.2平行四边形的判定巩固练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 496.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 19:47:00 | ||
图片预览



文档简介
2021-2022学年八年级下册数学巩固练习(人教版)
18.1.2 平行四边形的判定
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.四边形ABCD中,对角线AC,BD交于点O,给出下列四组条件:
①,;
②,;
③,;
④,.
一定能判定四边形ABCD是平行四边形的条件有( )
A.1组 B.2组 C.3组 D.4组
2.下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.有两对邻角互补的四边形为平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
3.如图,在四边形ABCD中,,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A. B. C. D.
4.如图,在中,E,F分别在BC,AD上,若想要使四边形AECF为平行四边形,需添加一个条件,这个条件不可以是( )
A. B. C. D.
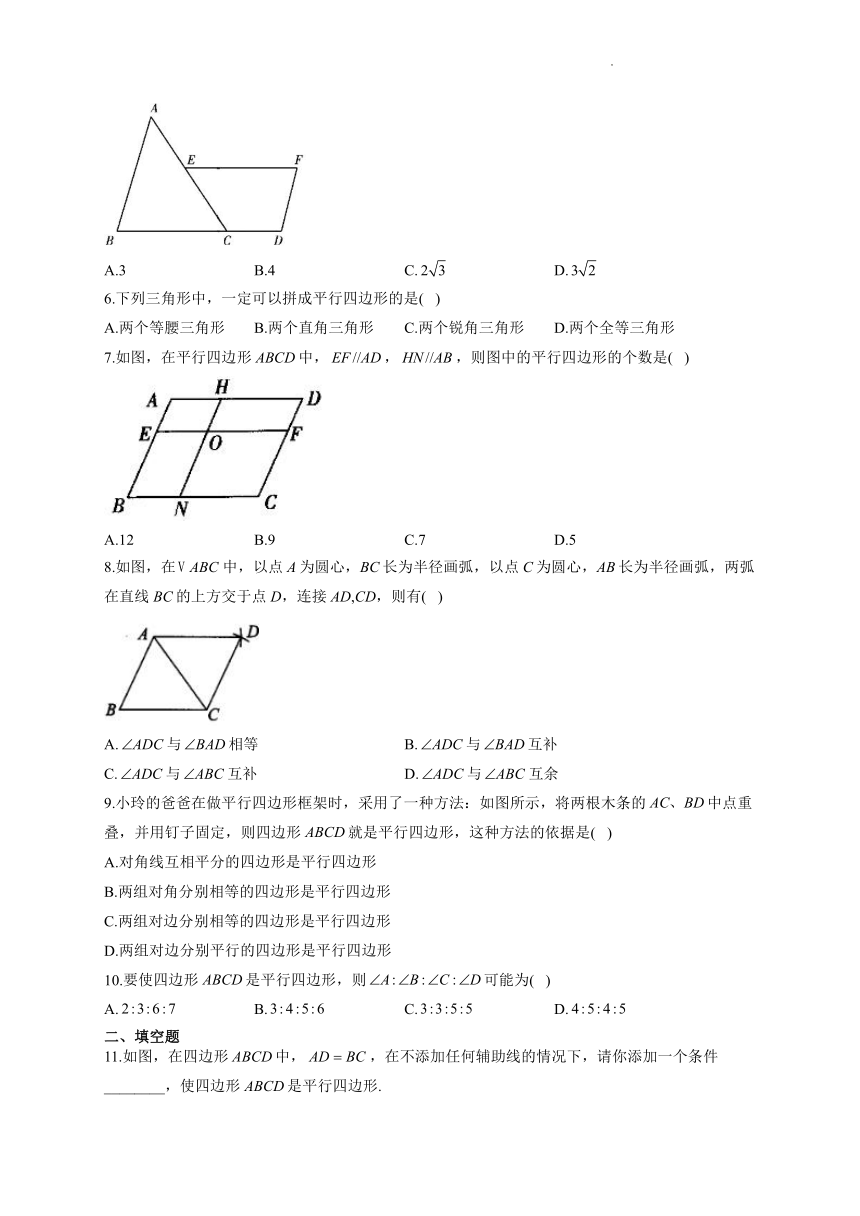
5.如图,在中,延长BC至D,使得,过AC的中点E作(点F位于点E右侧),且,连接DF.若,则DF的长为( )
A.3 B.4 C. D.
6.下列三角形中,一定可以拼成平行四边形的是( )
A.两个等腰三角形 B.两个直角三角形 C.两个锐角三角形 D.两个全等三角形
7.如图,在平行四边形ABCD中,,,则图中的平行四边形的个数是( )
A.12 B.9 C.7 D.5
8.如图,在中,以点A为圆心,BC长为半径画弧,以点C为圆心,AB长为半径画弧,两弧在直线BC的上方交于点D,连接AD,CD,则有( )
A.与相等 B.与互补
C.与互补 D.与互余
9.小玲的爸爸在做平行四边形框架时,采用了一种方法:如图所示,将两根木条的中点重叠,并用钉子固定,则四边形就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
10.要使四边形是平行四边形,则可能为( )
A. B. C. D.
二、填空题
11.如图,在四边形中,,在不添加任何辅助线的情况下,请你添加一个条件________,使四边形是平行四边形.
12.如图,四边形ABCD的对角线交于点O,从下列条件①,②,③,④中选出两个可使四边形ABCD是平行四边形,则你选的两个条件是____________.(填写一组序号即可)
13.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带来了两块碎玻璃,其编号应该是__________.
14.在平行四边形ABCD中,BC边上的高为4,,,则平行四边形ABCD的周长为________________.
15.如图,在平行四边形ABCD中, cm, cm,点P在AD边上以1 cm/s的速度从点A向点D运动,点Q在BC边上以4 cm/s的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动过程中,以P,D,Q,B四点为顶点组成平行四边形的次数有______次.
三、解答题
16.已知:如图,在中,E,F分别为边AD,BC上一点,且.求证:四边形AFCE是平行四边形.
17.如图,四边形ABCD的对角线AC,BD交于点O,已知点O是AC的中点,,.求证:四边形ABCD是平行四边形.
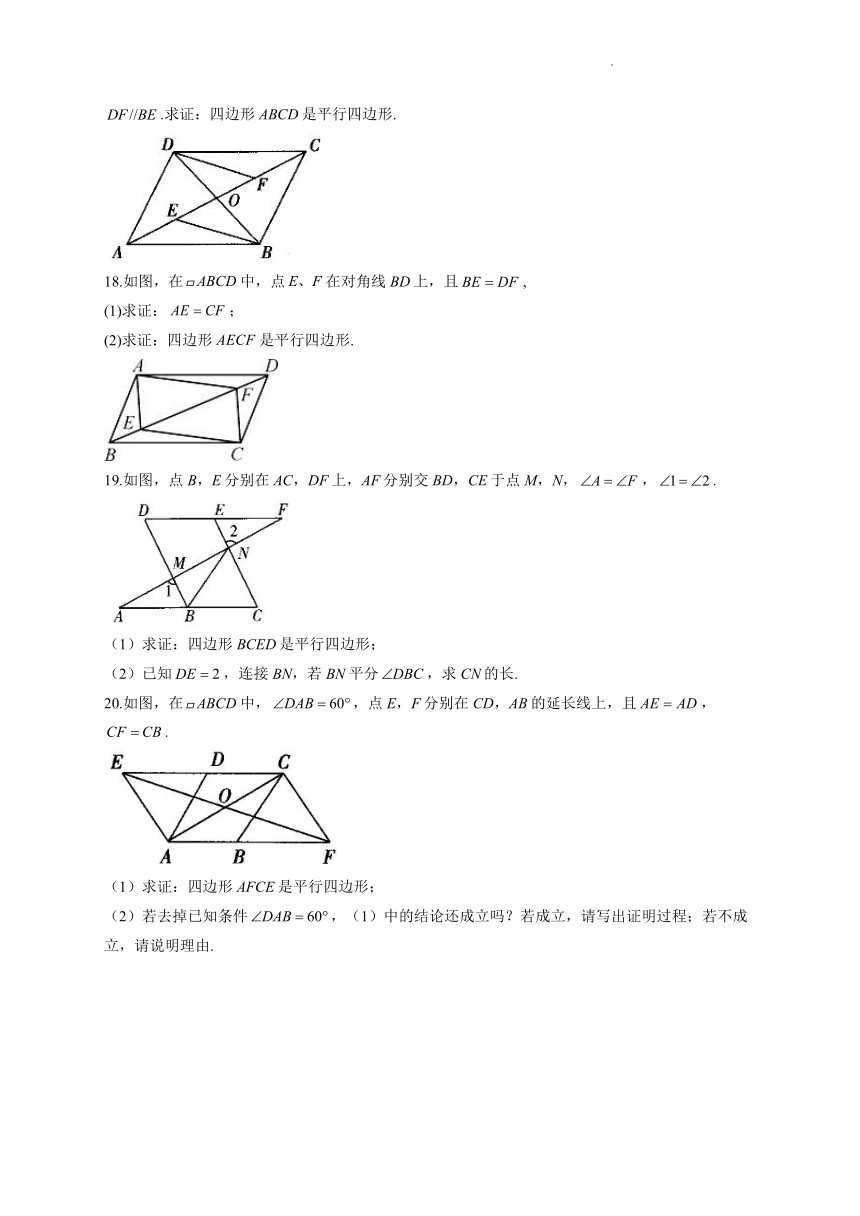
18.如图,在中,点在对角线BD上,且,
(1)求证:;
(2)求证:四边形是平行四边形.
19.如图,点B,E分别在AC,DF上,AF分别交BD,CE于点M,N,,.
(1)求证:四边形BCED是平行四边形;
(2)已知,连接BN,若BN平分,求CN的长.
20.如图,在中,,点E,F分别在CD,AB的延长线上,且,.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件,(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
参考答案
1.答案:C
解析:①根据两组对边分别平行的四边形是平行四边形,可判定四边形ABCD是平行四边形;②,,又,,,四边形ABCD是平行四边形;③根据对角线互相平分的四边形是平行四边形,可判定四边形ABCD是平行四边形;④由,,可得四边形ABCD是等腰梯形或平行四边形.综上所述,一定能判定四边形ABCD是平行四边形的有3组.故选C.
2.答案:B
解析:根据平行四边形的性质定理可得,A项正确;根据平行四边形的判定定理可得,C项正确;B项,在四边形ABCD中,若,,则只能推出,不一定是平行四边形,故B项错误;D项,在四边形ABCD中,若,,则,,四边形ABCD是平行四边形,故D项正确.故选B.
3.答案:B
解析:根据两组对边分别平行的四边形是平行四边形可补充条件:;根据一组对边平行且相等的四边形是平行四边形可补充条件:;由可得出,故,则补充条件能推理出四边形ABCD是平行四边形;补充条件不能得出四边形ABCD是平行四边形.故选B.
4.答案:B
解析:A项,由四边形ABCD是平行四边形,可得,结合,则四边形AECF是平行四边形,A项不合题意;B项,根据,可知四边形AECF可能是平行四边形,也可能是等腰梯形,B项符合题意;C项,由四边形ABCD是平行四边形,可得,,又因为,所以,则,因为,所以,又因为,所以四边形AECF是平行四边形,C项不合题意;D项,由,可得,结合,则四边形AECF是平行四边形,D项不合题意.故选B.
5.答案:B
解析:如图,取BC的中点G,连接EG. E是AC的中点,EG是的中位线,,设,则,,,,四边形EGDF是平行四边形,.故选B.
6.答案:D
解析:
7.答案:B
解析:根据两组对边分别平行的四边形叫做平行四边形,知图中的四边形AEOH、四边形HOFD、四边形EBNO、四边形ONCF、四边形AEFD、四边形EBCF、四边形ABNH、四边形HNCD、四边形ABCD都是平行四边形,共9个.故选B.
8.答案:B
解析:四边形ABCD是平行四边形, 与互补.故选B.
9.答案:A
解析:由已知可得,所以四边形是平行四边形,依据是对角线互相平分的四边形是平行四边形.故选A.
10.答案:D
解析:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,可知只有D正确.
11.答案:
解析:根据平行四边形的判定,可再添加一个条件:
故答案为:
12.答案:①③(答案不唯一)
解析:选的条件是①③.,,,在和中,,,,四边形ABCD是平行四边形.
13.答案:②③
解析:只有②③两块碎玻璃的两边互相平行,且中间部分相连,角的两边的延长线的交点就是平行四边形的顶点,带②③两块碎玻璃,就可以配到一块与原来相同的平行四边形玻璃 .
14.答案:12或20
解析:如图1,过点A作于点E,则,,,,,,,的周长为20;如图2,过点A作交BC的延长于点F,则,,,,,,,的周长为12.综上,的周长为12或20.
15.答案:3
解析:设经过t s,以P,D,Q,B四点为顶点组成平行四边形,则,分以下情况:①点Q的运动路线是,由题意得,此时,不符合题意;②点Q的运动路线是,由题意得,解得;③点Q的运动路线是,由题意得,解得;④点Q的运动路线是,由题意得,解得;⑤点Q的运动路线是,由题意得,解得,此时点P走的路程为,不符合题意.所以以P,D,Q,B四点为顶点组成平行四边形的次数为3次.
16.答案:证明:四边形ABCD是平行四边形,
,.
,F分别为边AD,BC上一点,且,
.
即AE=FC
四边形AFCE是平行四边形.
解析:
17.答案:点O是AC的中点,.
,.
,.
又,
,,
四边形ABCD是平行四边形.
解析:
18.答案:(1)四边形是平行四边形
在和中,
(2)由1可知
又
四边形是平行四边形.
解析:
19.答案:(1),,
,且,
,,
四边形BCED是平行四边形.
(2)BN平分,,
,,
,.
解析:
20.答案:(1)四边形ABCD是平行四边形,
,,
.
又,,
,都是等边三角形,
,.
又,,
,,
四边形AFCE是平行四边形.
(2)(1)中的结论仍然成立.证明如下:
四边形ABCD是平行四边形.
,.
,,
,,
,
又,,
,.
又,,即,
又,四边形AFCE是平行四边形.
解析:
18.1.2 平行四边形的判定
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.四边形ABCD中,对角线AC,BD交于点O,给出下列四组条件:
①,;
②,;
③,;
④,.
一定能判定四边形ABCD是平行四边形的条件有( )
A.1组 B.2组 C.3组 D.4组
2.下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.有两对邻角互补的四边形为平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
3.如图,在四边形ABCD中,,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A. B. C. D.
4.如图,在中,E,F分别在BC,AD上,若想要使四边形AECF为平行四边形,需添加一个条件,这个条件不可以是( )
A. B. C. D.
5.如图,在中,延长BC至D,使得,过AC的中点E作(点F位于点E右侧),且,连接DF.若,则DF的长为( )
A.3 B.4 C. D.
6.下列三角形中,一定可以拼成平行四边形的是( )
A.两个等腰三角形 B.两个直角三角形 C.两个锐角三角形 D.两个全等三角形
7.如图,在平行四边形ABCD中,,,则图中的平行四边形的个数是( )
A.12 B.9 C.7 D.5
8.如图,在中,以点A为圆心,BC长为半径画弧,以点C为圆心,AB长为半径画弧,两弧在直线BC的上方交于点D,连接AD,CD,则有( )
A.与相等 B.与互补
C.与互补 D.与互余
9.小玲的爸爸在做平行四边形框架时,采用了一种方法:如图所示,将两根木条的中点重叠,并用钉子固定,则四边形就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
10.要使四边形是平行四边形,则可能为( )
A. B. C. D.
二、填空题
11.如图,在四边形中,,在不添加任何辅助线的情况下,请你添加一个条件________,使四边形是平行四边形.
12.如图,四边形ABCD的对角线交于点O,从下列条件①,②,③,④中选出两个可使四边形ABCD是平行四边形,则你选的两个条件是____________.(填写一组序号即可)
13.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带来了两块碎玻璃,其编号应该是__________.
14.在平行四边形ABCD中,BC边上的高为4,,,则平行四边形ABCD的周长为________________.
15.如图,在平行四边形ABCD中, cm, cm,点P在AD边上以1 cm/s的速度从点A向点D运动,点Q在BC边上以4 cm/s的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动过程中,以P,D,Q,B四点为顶点组成平行四边形的次数有______次.
三、解答题
16.已知:如图,在中,E,F分别为边AD,BC上一点,且.求证:四边形AFCE是平行四边形.
17.如图,四边形ABCD的对角线AC,BD交于点O,已知点O是AC的中点,,.求证:四边形ABCD是平行四边形.
18.如图,在中,点在对角线BD上,且,
(1)求证:;
(2)求证:四边形是平行四边形.
19.如图,点B,E分别在AC,DF上,AF分别交BD,CE于点M,N,,.
(1)求证:四边形BCED是平行四边形;
(2)已知,连接BN,若BN平分,求CN的长.
20.如图,在中,,点E,F分别在CD,AB的延长线上,且,.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件,(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.
参考答案
1.答案:C
解析:①根据两组对边分别平行的四边形是平行四边形,可判定四边形ABCD是平行四边形;②,,又,,,四边形ABCD是平行四边形;③根据对角线互相平分的四边形是平行四边形,可判定四边形ABCD是平行四边形;④由,,可得四边形ABCD是等腰梯形或平行四边形.综上所述,一定能判定四边形ABCD是平行四边形的有3组.故选C.
2.答案:B
解析:根据平行四边形的性质定理可得,A项正确;根据平行四边形的判定定理可得,C项正确;B项,在四边形ABCD中,若,,则只能推出,不一定是平行四边形,故B项错误;D项,在四边形ABCD中,若,,则,,四边形ABCD是平行四边形,故D项正确.故选B.
3.答案:B
解析:根据两组对边分别平行的四边形是平行四边形可补充条件:;根据一组对边平行且相等的四边形是平行四边形可补充条件:;由可得出,故,则补充条件能推理出四边形ABCD是平行四边形;补充条件不能得出四边形ABCD是平行四边形.故选B.
4.答案:B
解析:A项,由四边形ABCD是平行四边形,可得,结合,则四边形AECF是平行四边形,A项不合题意;B项,根据,可知四边形AECF可能是平行四边形,也可能是等腰梯形,B项符合题意;C项,由四边形ABCD是平行四边形,可得,,又因为,所以,则,因为,所以,又因为,所以四边形AECF是平行四边形,C项不合题意;D项,由,可得,结合,则四边形AECF是平行四边形,D项不合题意.故选B.
5.答案:B
解析:如图,取BC的中点G,连接EG. E是AC的中点,EG是的中位线,,设,则,,,,四边形EGDF是平行四边形,.故选B.
6.答案:D
解析:
7.答案:B
解析:根据两组对边分别平行的四边形叫做平行四边形,知图中的四边形AEOH、四边形HOFD、四边形EBNO、四边形ONCF、四边形AEFD、四边形EBCF、四边形ABNH、四边形HNCD、四边形ABCD都是平行四边形,共9个.故选B.
8.答案:B
解析:四边形ABCD是平行四边形, 与互补.故选B.
9.答案:A
解析:由已知可得,所以四边形是平行四边形,依据是对角线互相平分的四边形是平行四边形.故选A.
10.答案:D
解析:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,可知只有D正确.
11.答案:
解析:根据平行四边形的判定,可再添加一个条件:
故答案为:
12.答案:①③(答案不唯一)
解析:选的条件是①③.,,,在和中,,,,四边形ABCD是平行四边形.
13.答案:②③
解析:只有②③两块碎玻璃的两边互相平行,且中间部分相连,角的两边的延长线的交点就是平行四边形的顶点,带②③两块碎玻璃,就可以配到一块与原来相同的平行四边形玻璃 .
14.答案:12或20
解析:如图1,过点A作于点E,则,,,,,,,的周长为20;如图2,过点A作交BC的延长于点F,则,,,,,,,的周长为12.综上,的周长为12或20.
15.答案:3
解析:设经过t s,以P,D,Q,B四点为顶点组成平行四边形,则,分以下情况:①点Q的运动路线是,由题意得,此时,不符合题意;②点Q的运动路线是,由题意得,解得;③点Q的运动路线是,由题意得,解得;④点Q的运动路线是,由题意得,解得;⑤点Q的运动路线是,由题意得,解得,此时点P走的路程为,不符合题意.所以以P,D,Q,B四点为顶点组成平行四边形的次数为3次.
16.答案:证明:四边形ABCD是平行四边形,
,.
,F分别为边AD,BC上一点,且,
.
即AE=FC
四边形AFCE是平行四边形.
解析:
17.答案:点O是AC的中点,.
,.
,.
又,
,,
四边形ABCD是平行四边形.
解析:
18.答案:(1)四边形是平行四边形
在和中,
(2)由1可知
又
四边形是平行四边形.
解析:
19.答案:(1),,
,且,
,,
四边形BCED是平行四边形.
(2)BN平分,,
,,
,.
解析:
20.答案:(1)四边形ABCD是平行四边形,
,,
.
又,,
,都是等边三角形,
,.
又,,
,,
四边形AFCE是平行四边形.
(2)(1)中的结论仍然成立.证明如下:
四边形ABCD是平行四边形.
,.
,,
,,
,
又,,
,.
又,,即,
又,四边形AFCE是平行四边形.
解析:
