2021—2022学年人教版八年级数学下册18.2.1矩形课后练习题(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.2.1矩形课后练习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 19:51:48 | ||
图片预览



文档简介
18.2.1矩形 课后练习题
一、选择题
1.矩形具有而一般平行四边形不具有的性质是( )
A.两组对边分别相等 B.两组对角分别相等
C.两条对角线互相平分 D.两条对角线相等
2.矩形具有而一般平行四边形不具有的性质是( )
A.对角线互相平分 B.对角相等
C.对边相等 D.对角线相等
3.在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③ B.①②④ C.②③④ D.①③④
4.如图,矩形ABCD的顶点A,B,C分别落在∠MON的边OM,ON上,若OA=OC,要求只用无刻度的直尺作∠MON的平分线.小明的作法如下:连接AC,BD交于点E,作射线OE,则射线OE平分∠MON.
有以下几条几何性质:
①矩形的四个角都是直角;②矩形的对角线互相平分;③等腰三角形的“三线合一”.
小明的作法依据是( )
A.①② B.①③ C.②③ D.①②③
5、如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
A.2对 B.3对 C.4对 D.5对
6.如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A. B.6 C.4 D.5
7.如图,矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为( )
A.10cm B.8cm C.6cm D.5cm
8.将一张矩形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是( )
A.75° B.63° C.55° D.45°
二、填空题
9.在Rt△ABC中,D是斜边AB的中点,AD=10,则CD的长是______.
10、如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是 。
11、Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .
12、一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为 平方厘米。
13.如图,平行四边形ABCD的顶点B在矩形AEFC的边EF上,点B与点E,F不重合,若△ACD的面积3,则图中阴影部分两个三角形的面积和为____________.
三、解答题
14.如图,在Rt△ABC中,∠B=90°,AB=4,BC=3,阴影部分是一个长方形,AE=1,求阴影部分的面积.
15.已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
(1)求证:△ABD≌△CAE.
(2)连结DE,线段DE与AB之间有怎样的位置关系和数量关系?请证明你的结论.
16.如图,矩形ABCD中,E、F分别为边AD和BC上的点,BE=DF,求证:DE=BF.
17.如图,在四边形ABCD中,∠B=∠C.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.
(1)求证:四边形AEFG是平行四边形;
(2)当∠FGC与∠EFB满足怎样的关系时,四边形AEFG是矩形.请说明理由.
18.如图,在 ABCD中,过点D作DF⊥BC于点F,点E在边AD上,AE=CF,连结BE、CE.
(1)求证:四边形BFDE是矩形.
(2)若DE=AB,∠ABC=130°,求∠DEC的度数.
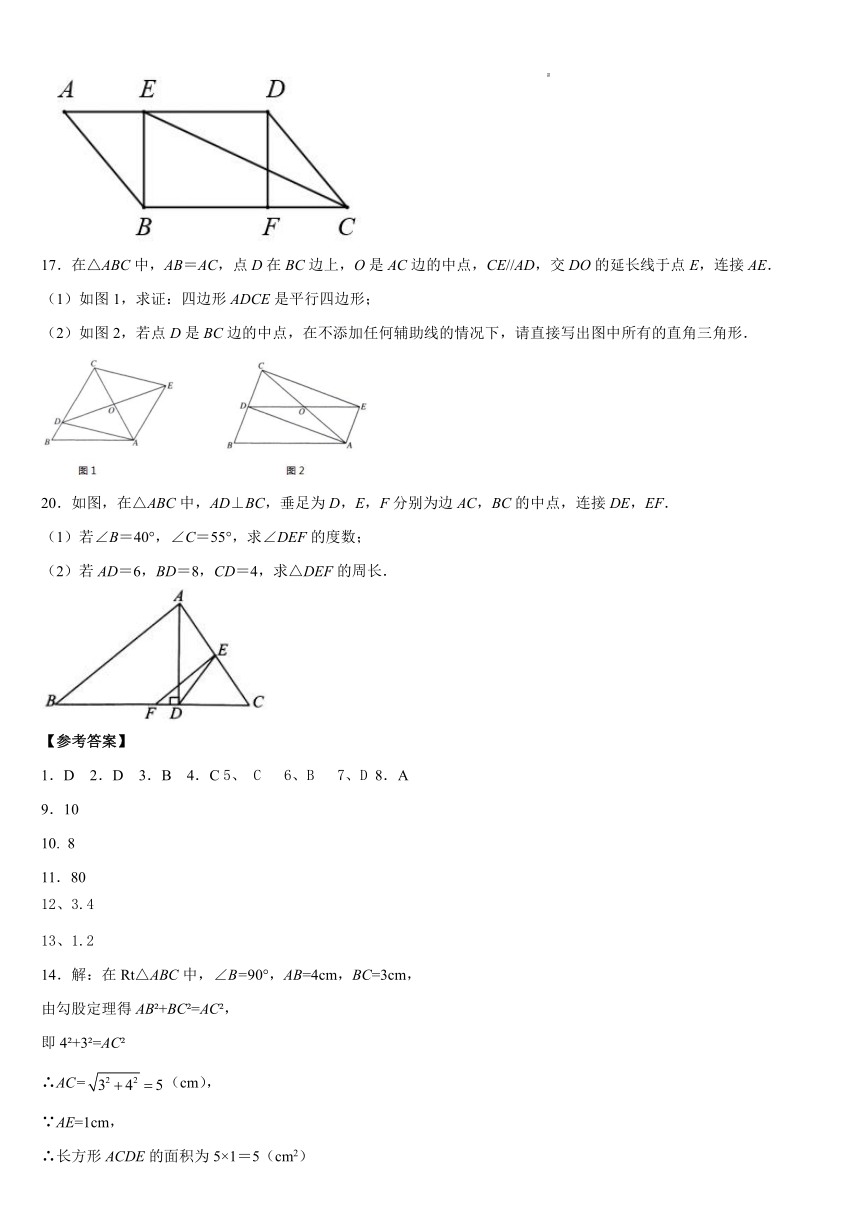
17.在△ABC中,AB=AC,点D在BC边上,O是AC边的中点,CE//AD,交DO的延长线于点E,连接AE.
(1)如图1,求证:四边形ADCE是平行四边形;
(2)如图2,若点D是BC边的中点,在不添加任何辅助线的情况下,请直接写出图中所有的直角三角形.
20.如图,在△ABC中,AD⊥BC,垂足为D,E,F分别为边AC,BC的中点,连接DE,EF.
(1)若∠B=40°,∠C=55°,求∠DEF的度数;
(2)若AD=6,BD=8,CD=4,求△DEF的周长.
【参考答案】
1.D 2.D 3.B 4.C 5、 C 6、B 7、D 8.A
9.10
8
11.80
12、3.4
13、1.2
14.解:在Rt△ABC中,∠B=90°,AB=4cm,BC=3cm,
由勾股定理得AB +BC =AC ,
即4 +3 =AC
∴AC=(cm),
∵AE=1cm,
∴长方形ACDE的面积为5×1=5(cm2)
15、4
16.解:在Rt△ABC中,CD是斜边AB上的中线,
∴AB=2CD=2,
由勾股定理得,BC= .
17(1)证明:在四边形ABCD中,∠B=∠C,
∵GF=GC,
∴∠C=∠GFC,∠B=∠GFC,
∴AB∥GF,即AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形.
(2)
解:当∠FGC=2∠EFB时,四边形AEFG是矩形;
∵∠FGC+∠GFC+∠C=180°,∠GFC=∠C,∠FGC=2∠EFB,
∴2∠GFC+2∠EFB=180°,
∴∠BFE+∠GFC=90°.
∴∠EFG=90°.
∵四边形AEFG是平行四边形,
∴四边形AEFG是矩形.
18.(1)证明:在 ABCD中,AD∥BC,AD=BC,
∴ED∥BF.
∵ED=AD AE,BF=BC CF,AE=CF,
∴ED=BF.
∴四边形BFDE是平行四边形.
∵DF⊥BC,
∴∠DFB=90°,
∴四边形BFDE是矩形;
(2)解:在 ABCD中,AB=CD,∠ABC=∠ADC.
∵DE=AB,∠ABC=130°,
∴DE=CD,∠ADC=130°.
∴∠DEC=×(180° 130°)=25°.
19.解:(1)∵CE//AD,
∴∠CED=∠ADE,
∵O是AC边的中点,
∴OA=OC,
∴在△COE和△AOD中,
,
∴△COE≌△AOD(AAS),
∴CE=AD,
又∵CE//AD,
∴四边形ADCE是平行四边形;
(2)∵点D是BC边的中点,
∴DC=DB,
又由(1)可知四边形ADCE是平行四边形,
∴DC=AE,DCAE,
∴DB=AE,
又∵DBAE,
∴四边形DBAE是平行四边形,
∴AB=DE,
又∵AB=AC,
∴DE=AC,
∵四边形ADCE是平行四边形,
∴平行四边形ADCE是矩形,
∴∠DCE=∠CEA=∠EAD=∠ADC=90°,
∴∠BDA=90°,
∴直接三角形有:.
20(1) E,F分别为边AC,BC的中点,
AD⊥BC
(2) AD⊥BC,AD=6,BD=8,CD=4,
E,F分别为边AC,BC的中点,
△DEF的周长为
一、选择题
1.矩形具有而一般平行四边形不具有的性质是( )
A.两组对边分别相等 B.两组对角分别相等
C.两条对角线互相平分 D.两条对角线相等
2.矩形具有而一般平行四边形不具有的性质是( )
A.对角线互相平分 B.对角相等
C.对边相等 D.对角线相等
3.在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③ B.①②④ C.②③④ D.①③④
4.如图,矩形ABCD的顶点A,B,C分别落在∠MON的边OM,ON上,若OA=OC,要求只用无刻度的直尺作∠MON的平分线.小明的作法如下:连接AC,BD交于点E,作射线OE,则射线OE平分∠MON.
有以下几条几何性质:
①矩形的四个角都是直角;②矩形的对角线互相平分;③等腰三角形的“三线合一”.
小明的作法依据是( )
A.①② B.①③ C.②③ D.①②③
5、如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
A.2对 B.3对 C.4对 D.5对
6.如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A. B.6 C.4 D.5
7.如图,矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为( )
A.10cm B.8cm C.6cm D.5cm
8.将一张矩形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是( )
A.75° B.63° C.55° D.45°
二、填空题
9.在Rt△ABC中,D是斜边AB的中点,AD=10,则CD的长是______.
10、如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是 。
11、Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .
12、一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为 平方厘米。
13.如图,平行四边形ABCD的顶点B在矩形AEFC的边EF上,点B与点E,F不重合,若△ACD的面积3,则图中阴影部分两个三角形的面积和为____________.
三、解答题
14.如图,在Rt△ABC中,∠B=90°,AB=4,BC=3,阴影部分是一个长方形,AE=1,求阴影部分的面积.
15.已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
(1)求证:△ABD≌△CAE.
(2)连结DE,线段DE与AB之间有怎样的位置关系和数量关系?请证明你的结论.
16.如图,矩形ABCD中,E、F分别为边AD和BC上的点,BE=DF,求证:DE=BF.
17.如图,在四边形ABCD中,∠B=∠C.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.
(1)求证:四边形AEFG是平行四边形;
(2)当∠FGC与∠EFB满足怎样的关系时,四边形AEFG是矩形.请说明理由.
18.如图,在 ABCD中,过点D作DF⊥BC于点F,点E在边AD上,AE=CF,连结BE、CE.
(1)求证:四边形BFDE是矩形.
(2)若DE=AB,∠ABC=130°,求∠DEC的度数.
17.在△ABC中,AB=AC,点D在BC边上,O是AC边的中点,CE//AD,交DO的延长线于点E,连接AE.
(1)如图1,求证:四边形ADCE是平行四边形;
(2)如图2,若点D是BC边的中点,在不添加任何辅助线的情况下,请直接写出图中所有的直角三角形.
20.如图,在△ABC中,AD⊥BC,垂足为D,E,F分别为边AC,BC的中点,连接DE,EF.
(1)若∠B=40°,∠C=55°,求∠DEF的度数;
(2)若AD=6,BD=8,CD=4,求△DEF的周长.
【参考答案】
1.D 2.D 3.B 4.C 5、 C 6、B 7、D 8.A
9.10
8
11.80
12、3.4
13、1.2
14.解:在Rt△ABC中,∠B=90°,AB=4cm,BC=3cm,
由勾股定理得AB +BC =AC ,
即4 +3 =AC
∴AC=(cm),
∵AE=1cm,
∴长方形ACDE的面积为5×1=5(cm2)
15、4
16.解:在Rt△ABC中,CD是斜边AB上的中线,
∴AB=2CD=2,
由勾股定理得,BC= .
17(1)证明:在四边形ABCD中,∠B=∠C,
∵GF=GC,
∴∠C=∠GFC,∠B=∠GFC,
∴AB∥GF,即AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形.
(2)
解:当∠FGC=2∠EFB时,四边形AEFG是矩形;
∵∠FGC+∠GFC+∠C=180°,∠GFC=∠C,∠FGC=2∠EFB,
∴2∠GFC+2∠EFB=180°,
∴∠BFE+∠GFC=90°.
∴∠EFG=90°.
∵四边形AEFG是平行四边形,
∴四边形AEFG是矩形.
18.(1)证明:在 ABCD中,AD∥BC,AD=BC,
∴ED∥BF.
∵ED=AD AE,BF=BC CF,AE=CF,
∴ED=BF.
∴四边形BFDE是平行四边形.
∵DF⊥BC,
∴∠DFB=90°,
∴四边形BFDE是矩形;
(2)解:在 ABCD中,AB=CD,∠ABC=∠ADC.
∵DE=AB,∠ABC=130°,
∴DE=CD,∠ADC=130°.
∴∠DEC=×(180° 130°)=25°.
19.解:(1)∵CE//AD,
∴∠CED=∠ADE,
∵O是AC边的中点,
∴OA=OC,
∴在△COE和△AOD中,
,
∴△COE≌△AOD(AAS),
∴CE=AD,
又∵CE//AD,
∴四边形ADCE是平行四边形;
(2)∵点D是BC边的中点,
∴DC=DB,
又由(1)可知四边形ADCE是平行四边形,
∴DC=AE,DCAE,
∴DB=AE,
又∵DBAE,
∴四边形DBAE是平行四边形,
∴AB=DE,
又∵AB=AC,
∴DE=AC,
∵四边形ADCE是平行四边形,
∴平行四边形ADCE是矩形,
∴∠DCE=∠CEA=∠EAD=∠ADC=90°,
∴∠BDA=90°,
∴直接三角形有:.
20(1) E,F分别为边AC,BC的中点,
AD⊥BC
(2) AD⊥BC,AD=6,BD=8,CD=4,
E,F分别为边AC,BC的中点,
△DEF的周长为
