2021-2022学年人教版八年级数学下册18.2.1矩形课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.2.1矩形课时练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 174.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 00:00:00 | ||
图片预览


文档简介
18.2.1《矩形》课时练习
一、选择题
1.对角线相等且互相平分的四边形是( )
A.一般四边形 B.平行四边形 C.矩形 D.菱形
2.下列三个命题中,是真命题的有( )
①对角线相等的四边形是矩形;
②三个角是直角的四边形是矩形;
③有一个角是直角的平行四边形是矩形.
A.3个 B.2个 C.1个 D.0个
3.如图所示,矩形ABCD中,BC=2AB,E为BC上的一点,且AE=AD,则∠EDC的度数是( )
A.30° B.75° C.45° D.15°
4.如图,在长方形内画了一些直线,已知边上有三块面积分别是12、32、52,那么图中阴影部分的面积是( )
A.108 B.96 C.84 D.72
5.如图,矩形ABCD中,∠BOC=120°,BD=12,点P是AD边上一动点,则OP的最小值为( )
A.3 B.4 C.5 D.6
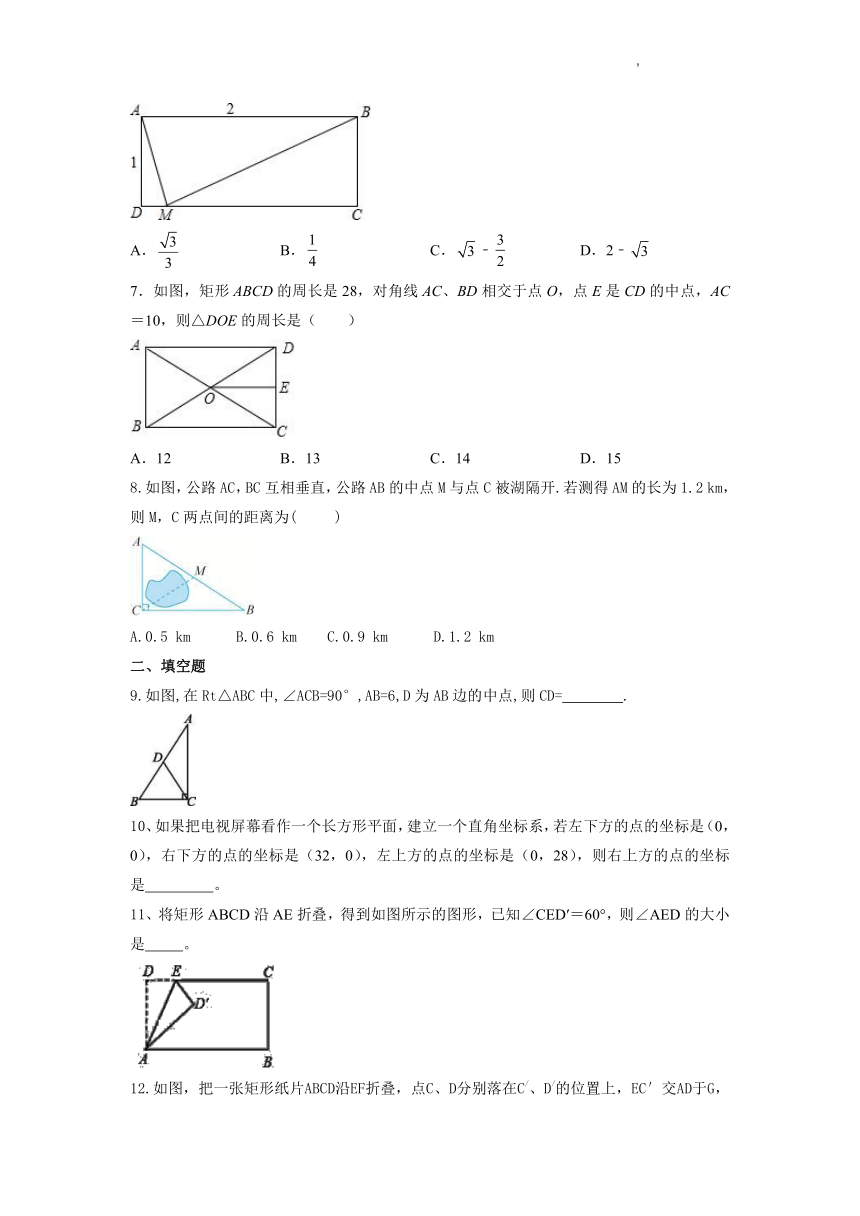
6.矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
A. B. C.﹣ D.2﹣
7.如图,矩形ABCD的周长是28,对角线AC、BD相交于点O,点E是CD的中点,AC=10,则△DOE的周长是( )
A.12 B.13 C.14 D.15
8.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2 km,则M,C两点间的距离为( )
A.0.5 km B.0.6 km C.0.9 km D.1.2 km
二、填空题
9.如图,在Rt△ABC中,∠ACB=90°,AB=6,D为AB边的中点,则CD= .
10、如果把电视屏幕看作一个长方形平面,建立一个直角坐标系,若左下方的点的坐标是(0,0),右下方的点的坐标是(32,0),左上方的点的坐标是(0,28),则右上方的点的坐标是 。
11、将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠AED的大小是 。
12.如图,把一张矩形纸片ABCD沿EF折叠,点C、D分别落在C/、D/的位置上,EC′交AD于G,已知∠EFG=56°,那么∠BEG= .
13.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠ACD的度数为 .
14.如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE、BD于点P,过点P作PQ⊥BC于点Q,则PQ= .
三、解答题
15.如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
16.如图,在△ABC中,AE∥BC,AB=AC,D为BC中点,AE=BD.
(1)求证:四边形AEBD是矩形.
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,直接写出EF的长.
17.如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=6,BC=18,求△BDE的面积.
18.如图,已知矩形中,是上的点,是上的一点,,且,cm.
(1)求证:;
(2)若cm,求的长.
19.如图,在 ABCD中,过点D作DF⊥BC于点F,点E在边AD上,AE=CF,连结BE、CE.
(1)求证:四边形BFDE是矩形.
(2)若DE=AB,∠ABC=130°,求∠DEC的度数.
20.如图,为矩形的对角线,于点,于点.
(1)求证:.
(2)求证:四边形是平行四边形.
参考答案
1.C 2.B 3.C 4.B 5.A 6.D 7.A 8.D
9.3
10、(32,28)
11、60°
12.:68°
13.:67.5°,
14..
15、(1)证明:∵四边形ABCD是矩形,∴∠B=∠C=∠ADC=90°,
AB=DC=7,BC=AD=12,∴∠BAF+∠AFB=90°,
∵DF平分∠ADC,∴∠ADF=∠CDF=45°,∴△DCF是等腰直角三角形,
∴FC=DC=7,∴AB=FC,
∵AF⊥EF,∴∠AFE=90°,∴∠AFB+∠EFC=90°,∴∠BAF=∠EFC,
∴△ABF≌△FCE(ASA), ∴EF=AF
(2)
16、5
17.提示:证明△BFE≌△CED,
从而BE=DC=AB,
∴∠BAE=45°,
可得AE平分∠BAD
18.(1)证明:,
.
.
四边形是矩形,
.
.
.
,
.
.
(2)解:,
.
,,
.
(cm).
19.(1)证明:在 ABCD中,AD∥BC,AD=BC,
∴ED∥BF.
∵ED=AD AE,BF=BC CF,AE=CF,
∴ED=BF.
∴四边形BFDE是平行四边形.
∵DF⊥BC,
∴∠DFB=90°,
∴四边形BFDE是矩形;
(2)解:在 ABCD中,AB=CD,∠ABC=∠ADC.
∵DE=AB,∠ABC=130°,
∴DE=CD,∠ADC=130°.
∴∠DEC=×(180° 130°)=25°.
20.解:(1)∵四边形ABCD是矩形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
又BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
∴△ABE≌△CDF(ASA).
(2)∵△ABE≌△CDF,
∴BE=DF.
又BE⊥AC,DF⊥AC,
∴BE∥DF.
∴四边形BFDE是平行四边形.
一、选择题
1.对角线相等且互相平分的四边形是( )
A.一般四边形 B.平行四边形 C.矩形 D.菱形
2.下列三个命题中,是真命题的有( )
①对角线相等的四边形是矩形;
②三个角是直角的四边形是矩形;
③有一个角是直角的平行四边形是矩形.
A.3个 B.2个 C.1个 D.0个
3.如图所示,矩形ABCD中,BC=2AB,E为BC上的一点,且AE=AD,则∠EDC的度数是( )
A.30° B.75° C.45° D.15°
4.如图,在长方形内画了一些直线,已知边上有三块面积分别是12、32、52,那么图中阴影部分的面积是( )
A.108 B.96 C.84 D.72
5.如图,矩形ABCD中,∠BOC=120°,BD=12,点P是AD边上一动点,则OP的最小值为( )
A.3 B.4 C.5 D.6
6.矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
A. B. C.﹣ D.2﹣
7.如图,矩形ABCD的周长是28,对角线AC、BD相交于点O,点E是CD的中点,AC=10,则△DOE的周长是( )
A.12 B.13 C.14 D.15
8.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2 km,则M,C两点间的距离为( )
A.0.5 km B.0.6 km C.0.9 km D.1.2 km
二、填空题
9.如图,在Rt△ABC中,∠ACB=90°,AB=6,D为AB边的中点,则CD= .
10、如果把电视屏幕看作一个长方形平面,建立一个直角坐标系,若左下方的点的坐标是(0,0),右下方的点的坐标是(32,0),左上方的点的坐标是(0,28),则右上方的点的坐标是 。
11、将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠AED的大小是 。
12.如图,把一张矩形纸片ABCD沿EF折叠,点C、D分别落在C/、D/的位置上,EC′交AD于G,已知∠EFG=56°,那么∠BEG= .
13.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠ACD的度数为 .
14.如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE、BD于点P,过点P作PQ⊥BC于点Q,则PQ= .
三、解答题
15.如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
16.如图,在△ABC中,AE∥BC,AB=AC,D为BC中点,AE=BD.
(1)求证:四边形AEBD是矩形.
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,直接写出EF的长.
17.如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=6,BC=18,求△BDE的面积.
18.如图,已知矩形中,是上的点,是上的一点,,且,cm.
(1)求证:;
(2)若cm,求的长.
19.如图,在 ABCD中,过点D作DF⊥BC于点F,点E在边AD上,AE=CF,连结BE、CE.
(1)求证:四边形BFDE是矩形.
(2)若DE=AB,∠ABC=130°,求∠DEC的度数.
20.如图,为矩形的对角线,于点,于点.
(1)求证:.
(2)求证:四边形是平行四边形.
参考答案
1.C 2.B 3.C 4.B 5.A 6.D 7.A 8.D
9.3
10、(32,28)
11、60°
12.:68°
13.:67.5°,
14..
15、(1)证明:∵四边形ABCD是矩形,∴∠B=∠C=∠ADC=90°,
AB=DC=7,BC=AD=12,∴∠BAF+∠AFB=90°,
∵DF平分∠ADC,∴∠ADF=∠CDF=45°,∴△DCF是等腰直角三角形,
∴FC=DC=7,∴AB=FC,
∵AF⊥EF,∴∠AFE=90°,∴∠AFB+∠EFC=90°,∴∠BAF=∠EFC,
∴△ABF≌△FCE(ASA), ∴EF=AF
(2)
16、5
17.提示:证明△BFE≌△CED,
从而BE=DC=AB,
∴∠BAE=45°,
可得AE平分∠BAD
18.(1)证明:,
.
.
四边形是矩形,
.
.
.
,
.
.
(2)解:,
.
,,
.
(cm).
19.(1)证明:在 ABCD中,AD∥BC,AD=BC,
∴ED∥BF.
∵ED=AD AE,BF=BC CF,AE=CF,
∴ED=BF.
∴四边形BFDE是平行四边形.
∵DF⊥BC,
∴∠DFB=90°,
∴四边形BFDE是矩形;
(2)解:在 ABCD中,AB=CD,∠ABC=∠ADC.
∵DE=AB,∠ABC=130°,
∴DE=CD,∠ADC=130°.
∴∠DEC=×(180° 130°)=25°.
20.解:(1)∵四边形ABCD是矩形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
又BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
∴△ABE≌△CDF(ASA).
(2)∵△ABE≌△CDF,
∴BE=DF.
又BE⊥AC,DF⊥AC,
∴BE∥DF.
∴四边形BFDE是平行四边形.
