2021-2022学年人教版八年级下册数学18.2.2菱形同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级下册数学18.2.2菱形同步练习(Word版含答案) | 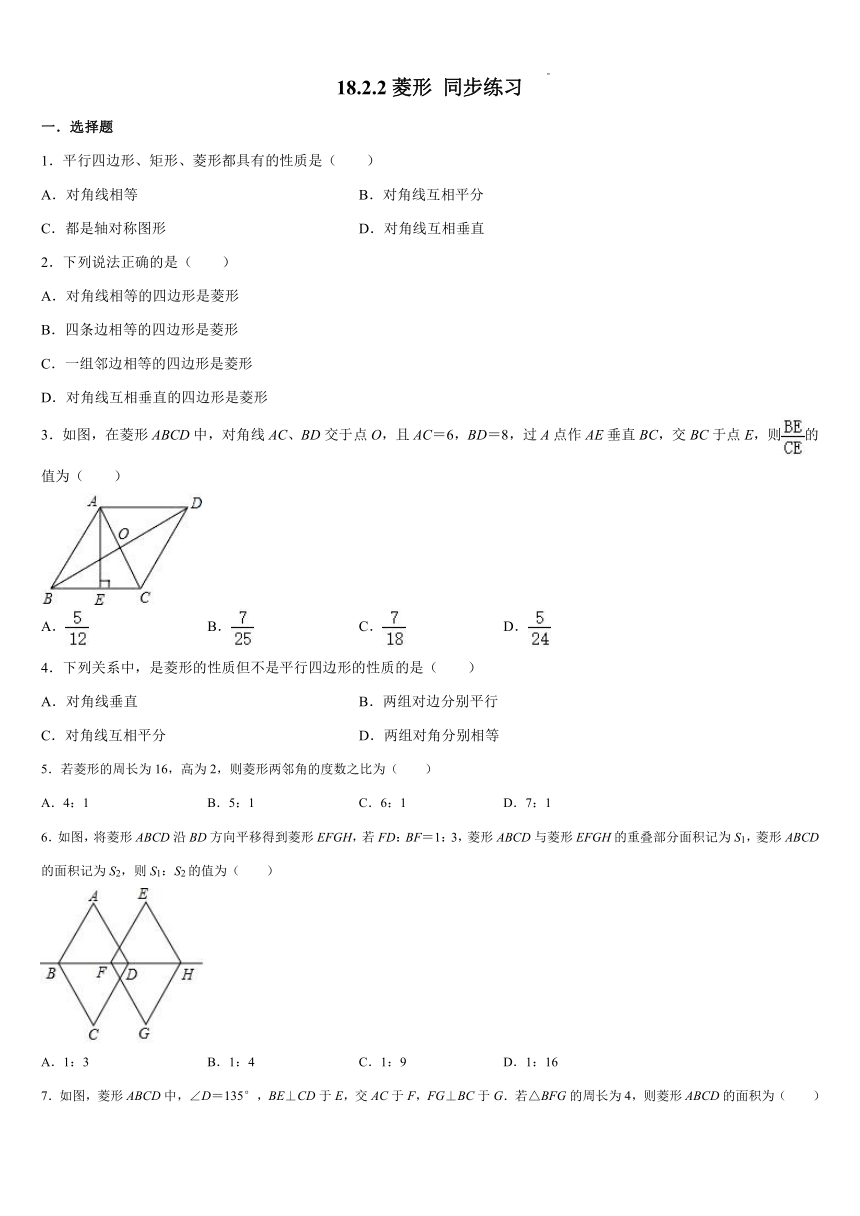 | |
| 格式 | docx | ||
| 文件大小 | 120.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 20:09:35 | ||
图片预览


文档简介
18.2.2菱形 同步练习
一.选择题
1.平行四边形、矩形、菱形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.都是轴对称图形 D.对角线互相垂直
2.下列说法正确的是( )
A.对角线相等的四边形是菱形
B.四条边相等的四边形是菱形
C.一组邻边相等的四边形是菱形
D.对角线互相垂直的四边形是菱形
3.如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为( )
A. B. C. D.
4.下列关系中,是菱形的性质但不是平行四边形的性质的是( )
A.对角线垂直 B.两组对边分别平行
C.对角线互相平分 D.两组对角分别相等
5.若菱形的周长为16,高为2,则菱形两邻角的度数之比为( )
A.4:1 B.5:1 C.6:1 D.7:1
6.如图,将菱形ABCD沿BD方向平移得到菱形EFGH,若FD:BF=1:3,菱形ABCD与菱形EFGH的重叠部分面积记为S1,菱形ABCD的面积记为S2,则S1:S2的值为( )
A.1:3 B.1:4 C.1:9 D.1:16
7.如图,菱形ABCD中,∠D=135°,BE⊥CD于E,交AC于F,FG⊥BC于G.若△BFG的周长为4,则菱形ABCD的面积为( )
A.4 B.8 C.16 D.16
8.如图,菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB.若NF=4,NM=8,ME=8,则AN等于( )
A.6 B.8 C.10 D.12
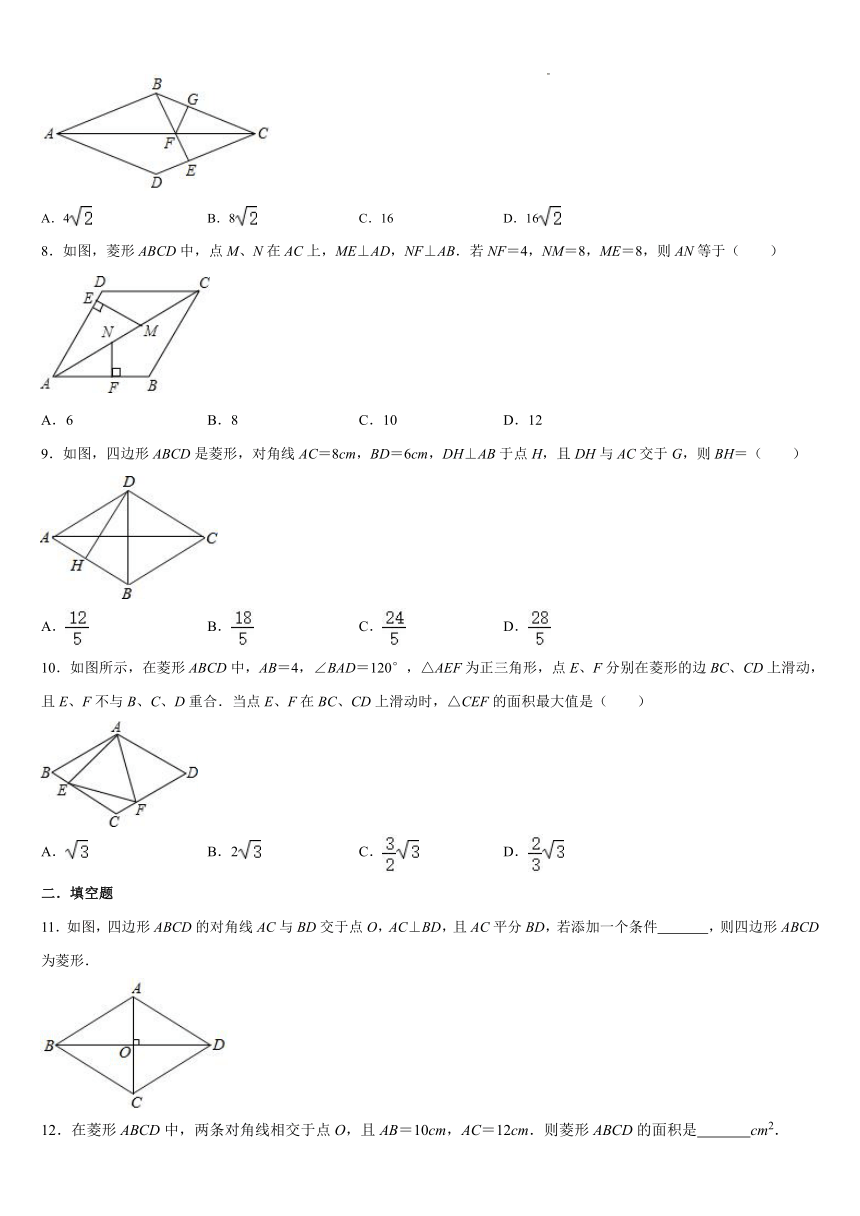
9.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则BH=( )
A. B. C. D.
10.如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,△CEF的面积最大值是( )
A. B.2 C. D.
二.填空题
11.如图,四边形ABCD的对角线AC与BD交于点O,AC⊥BD,且AC平分BD,若添加一个条件 ,则四边形ABCD为菱形.
12.在菱形ABCD中,两条对角线相交于点O,且AB=10cm,AC=12cm.则菱形ABCD的面积是 cm2.
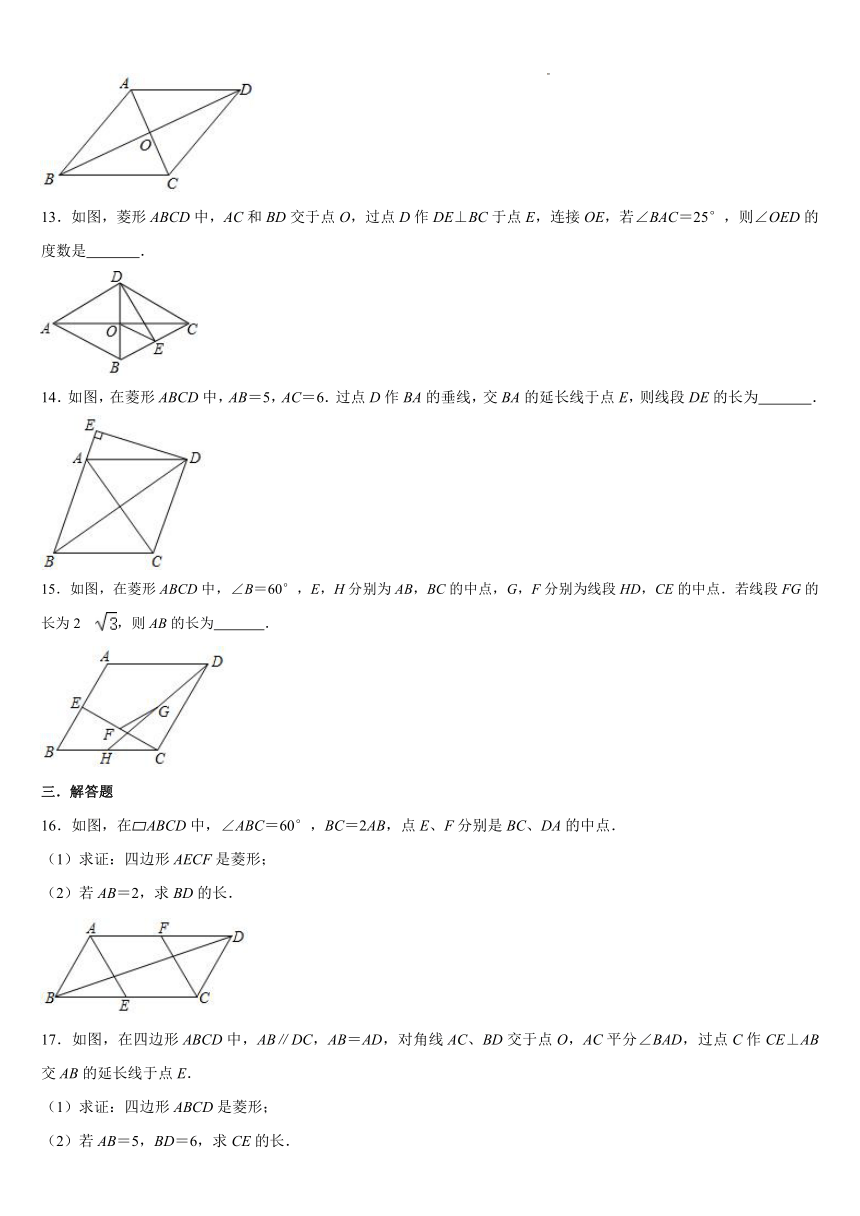
13.如图,菱形ABCD中,AC和BD交于点O,过点D作DE⊥BC于点E,连接OE,若∠BAC=25°,则∠OED的度数是 .
14.如图,在菱形ABCD中,AB=5,AC=6.过点D作BA的垂线,交BA的延长线于点E,则线段DE的长为 .
15.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2 ,则AB的长为 .
三.解答题
16.如图,在 ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、DA的中点.
(1)求证:四边形AECF是菱形;
(2)若AB=2,求BD的长.
17.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC、BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,BD=6,求CE的长.
18.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且2DE=AC,连接AE交OD于点F,连接DE、OE.
(1)求证:AF=EF;
(2)已知AB=2,若AB=2DE,求AE的长.
参考答案
一.选择题
1.B 2.B 3.C 4.A 5.B 6.D 7.B 8.B 9.B 10.A
11.OA=OC(答案不唯一).
12.96.
13.25°.
14..
15.8.
16.(1)证明:∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.
∵E,F分别是BC,AD的中点
∴BE=CE=BC,AF=AD,
∴CE=AF,CE∥AF,
∴四边形AECF是平行四边形,
∵BC=2AB,
∴AB=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AE=BE=CE,
∴平行四边形AECF是菱形;
(2)解:作BG⊥AD于G,如图所示:
则∠ABG=90°﹣∠ABC=30°,
∴AG=AB=1,BG=AG=,
∵AD=BC=2AB=4,
∴DG=AG+AD=5,
∴BD===2.
17.(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,OB=OD=BD=3,
∴OA===4,
∴AC=2OA=8,
∴菱形ABCD的面积=AC×BD=×8×6=24,
∵CE⊥AB,
∴菱形ABCD的面积=AB×CE=5CE=24,
∴CE=.
18.(1)证明:∵四边形ABCD是菱形,
∴OA=OC=AC,
∵2DE=AC,
∴DE=OA,
又∵DE∥AC,
∴四边形OADE是平行四边形,
∴AF=EF;
(2)解:连接CE,
∵DE∥OC,DE=OC,
∴四边形OCED是平行四边形,
又∵菱形ABCD,
∴AC⊥BD,
∴四边形OCED是矩形,
∴∠OCE=90°,
又∵AB=2DE=AC,
∴△ABC为等边三角形,
∵在菱形ABCD中,∠ABC=60°,
∴AC=AB=2,AO=AC=1,
∴在矩形OCED中,CE=OD==,
∴在Rt△ACE中,
AE==.
一.选择题
1.平行四边形、矩形、菱形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.都是轴对称图形 D.对角线互相垂直
2.下列说法正确的是( )
A.对角线相等的四边形是菱形
B.四条边相等的四边形是菱形
C.一组邻边相等的四边形是菱形
D.对角线互相垂直的四边形是菱形
3.如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为( )
A. B. C. D.
4.下列关系中,是菱形的性质但不是平行四边形的性质的是( )
A.对角线垂直 B.两组对边分别平行
C.对角线互相平分 D.两组对角分别相等
5.若菱形的周长为16,高为2,则菱形两邻角的度数之比为( )
A.4:1 B.5:1 C.6:1 D.7:1
6.如图,将菱形ABCD沿BD方向平移得到菱形EFGH,若FD:BF=1:3,菱形ABCD与菱形EFGH的重叠部分面积记为S1,菱形ABCD的面积记为S2,则S1:S2的值为( )
A.1:3 B.1:4 C.1:9 D.1:16
7.如图,菱形ABCD中,∠D=135°,BE⊥CD于E,交AC于F,FG⊥BC于G.若△BFG的周长为4,则菱形ABCD的面积为( )
A.4 B.8 C.16 D.16
8.如图,菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB.若NF=4,NM=8,ME=8,则AN等于( )
A.6 B.8 C.10 D.12
9.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则BH=( )
A. B. C. D.
10.如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,△CEF的面积最大值是( )
A. B.2 C. D.
二.填空题
11.如图,四边形ABCD的对角线AC与BD交于点O,AC⊥BD,且AC平分BD,若添加一个条件 ,则四边形ABCD为菱形.
12.在菱形ABCD中,两条对角线相交于点O,且AB=10cm,AC=12cm.则菱形ABCD的面积是 cm2.
13.如图,菱形ABCD中,AC和BD交于点O,过点D作DE⊥BC于点E,连接OE,若∠BAC=25°,则∠OED的度数是 .
14.如图,在菱形ABCD中,AB=5,AC=6.过点D作BA的垂线,交BA的延长线于点E,则线段DE的长为 .
15.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2 ,则AB的长为 .
三.解答题
16.如图,在 ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、DA的中点.
(1)求证:四边形AECF是菱形;
(2)若AB=2,求BD的长.
17.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC、BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,BD=6,求CE的长.
18.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且2DE=AC,连接AE交OD于点F,连接DE、OE.
(1)求证:AF=EF;
(2)已知AB=2,若AB=2DE,求AE的长.
参考答案
一.选择题
1.B 2.B 3.C 4.A 5.B 6.D 7.B 8.B 9.B 10.A
11.OA=OC(答案不唯一).
12.96.
13.25°.
14..
15.8.
16.(1)证明:∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.
∵E,F分别是BC,AD的中点
∴BE=CE=BC,AF=AD,
∴CE=AF,CE∥AF,
∴四边形AECF是平行四边形,
∵BC=2AB,
∴AB=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AE=BE=CE,
∴平行四边形AECF是菱形;
(2)解:作BG⊥AD于G,如图所示:
则∠ABG=90°﹣∠ABC=30°,
∴AG=AB=1,BG=AG=,
∵AD=BC=2AB=4,
∴DG=AG+AD=5,
∴BD===2.
17.(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,OB=OD=BD=3,
∴OA===4,
∴AC=2OA=8,
∴菱形ABCD的面积=AC×BD=×8×6=24,
∵CE⊥AB,
∴菱形ABCD的面积=AB×CE=5CE=24,
∴CE=.
18.(1)证明:∵四边形ABCD是菱形,
∴OA=OC=AC,
∵2DE=AC,
∴DE=OA,
又∵DE∥AC,
∴四边形OADE是平行四边形,
∴AF=EF;
(2)解:连接CE,
∵DE∥OC,DE=OC,
∴四边形OCED是平行四边形,
又∵菱形ABCD,
∴AC⊥BD,
∴四边形OCED是矩形,
∴∠OCE=90°,
又∵AB=2DE=AC,
∴△ABC为等边三角形,
∵在菱形ABCD中,∠ABC=60°,
∴AC=AB=2,AO=AC=1,
∴在矩形OCED中,CE=OD==,
∴在Rt△ACE中,
AE==.
