北师大版八年级数学下册 第三章 图形的平移与旋转 复习 课件(共27张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 第三章 图形的平移与旋转 复习 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 507.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 20:51:07 | ||
图片预览







文档简介
(共27张PPT)
第三章 图形的平移与旋转 复习课件
学习目标(1分钟)
2、会利用性质作图。
3、能够综合运用平移、旋转、轴对称的性质解决实际问题。
1、巩固平移、旋转、中心对称的相关概念及基本性质;
自学指导1(1分钟)
2.平移、旋转、中心对称各有哪些性质特征?
1.平移的两要素是:__________________。
旋转的三要素是:_____________________________。
平移方向和平移距离
旋转中心、旋转方向和旋转角度
3.图形的平移与坐标变化的规律怎样?
左右平移,___坐标改变,左____,右____。
上下平移,___坐标改变,上____,下____。
如果先左(右)平移,再上(下)平移时,横、纵坐标都要改变,此时可以看成是一次平移,平移的方向是_______________________平移的距离是__________________。
横
纵
减
减
加
加
对应点的连线所在的直线
对应点的连线的长度
自学检测1(7分钟)
1.下列标志中,可以看作是中心对称图形的是( )
A.
B.
C.
D.
D
2.观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
B
3.如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )
C
D.180°
C.120°
B.90°
A.60°
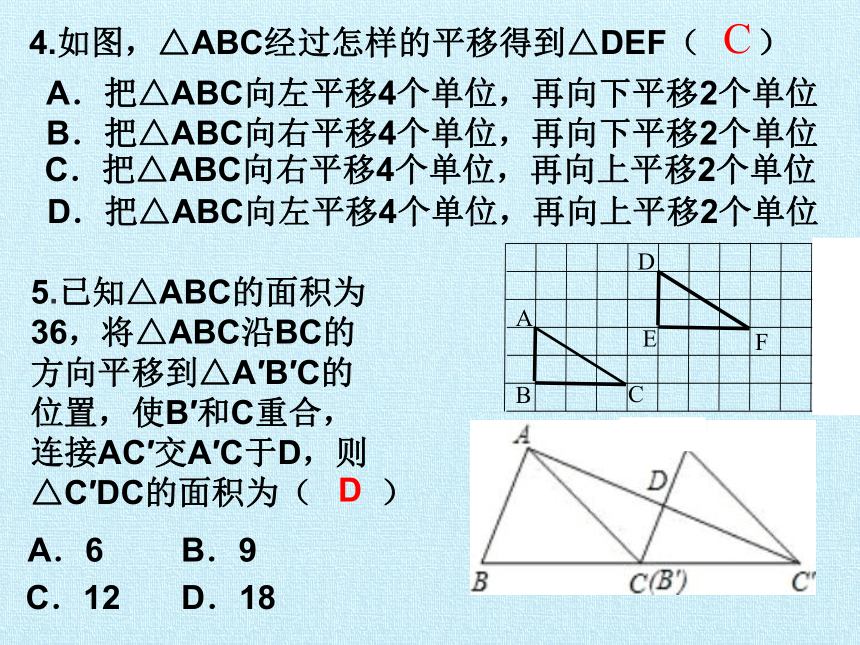
5.已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为( )
C.12
D.18
B.9
A.6
D
A.把△ABC向左平移4个单位,再向下平移2个单位
B.把△ABC向右平移4个单位,再向下平移2个单位
C
4.如图,△ABC经过怎样的平移得到△DEF( )
C.把△ABC向右平移4个单位,再向上平移2个单位
D.把△ABC向左平移4个单位,再向上平移2个单位
6.如图,将一朵小花放置在平面直角坐标系第一象限内,先将它向下平移4个单位后,再将它绕原点O旋转180°,则小花顶点A的对应点A′的坐标为 。
7.在数轴上,点A向右平移1个单位,再向左平移2个单位,再向右平移3个单位,再向左平移4个单位…100次平移后A所在点表示的数为2006,则点A的原始数为 。
2056
(-3,3)
自学指导2(1分钟)
1.思考下列问题:
平移、旋转、中心对称的作图方法是什么?
平移、旋转、中心对称作图时,分别要确定哪些条件?
2.自学例题,掌握解题方法和技巧,灵活运用图形变换的基本性质解决实际问题。
例题:如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( )
A.1: B.1:2 C. :2 D.1:
B
分析:解决本题关键要突破三点:
1.△APB≌△CP/B得AP=CP/
2.△APP/是直角三角形
3.△PBP/是等腰直角三角形
自学检测2(5分钟)
1.下列说法错误的有( )
①图形在平移过程中,图形上的每一点都移动了相同的距离;
②图形在旋转过程中,图形上的每一点都绕旋转中心转过了同样长的路程;
③中心对称图形的对称中心只有1个,而轴对称图形的对称轴可能不止一条;
④等边三角形既是轴对称图形,又是中心对称图形。
A.1个
B.2个
C.3个
D.4个
B
2.如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
D.格点Q
C.格点P
B.格点N
A.点M
B
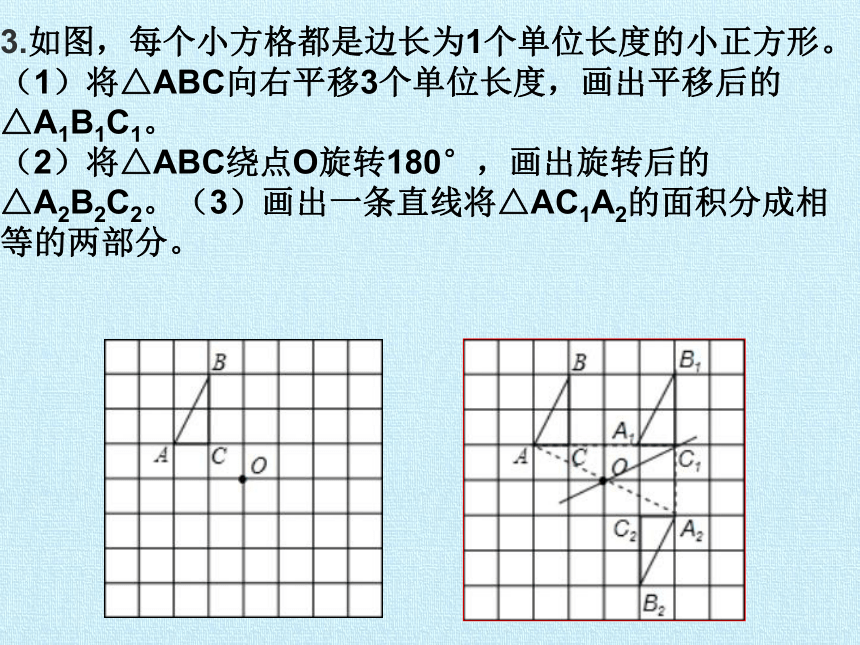
3.如图,每个小方格都是边长为1个单位长度的小正方形。
(1)将△ABC向右平移3个单位长度,画出平移后的△A1B1C1。
(2)将△ABC绕点O旋转180°,画出旋转后的△A2B2C2。(3)画出一条直线将△AC1A2的面积分成相等的两部分。
5.如图2所示,在平面内将Rt△ABC绕直角顶点C逆
时针旋转90°得到Rt△EFC。若AB=
BE的长为 。
,BC=1,则线段
3
4.如图1,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转一定的角度后能与△CBP′重合。若PB=3,则PP′= 。
图1 P′
图2
(2013 黄石) 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
C.4
B.5
B
解决此题关键是判断出△ACO是等腰直角三角形。
先求出∠ACD=30°,再根据旋转角求出∠ACD1=45°。
讨论、更正、点拨(4分钟)
点拨:
本题用到重要的知识点:1.旋转的性质,2.勾股定理,3.直角三角形中斜边上的中线等于斜边的一半。
一、考点:
1.平移、旋转、对称的基本性质
2.网格作图
3.基本性质的应用
二、难点:
1.旋转作图
2.图形的旋转与证明
三、易错、易漏点:
1.中心对称与中心对称图形的概念
2.旋转作图
3.中心对称与轴对称
4.图形的平移与坐标变化关系
5.旋转具有三要素,缺一不可
平移的基本性质:
①对应线段平行且相等;
②对应角相等
③对应点的连线平行 且相等
旋转的基本性质:
①对应线段相等,对应角相等
②对应点到旋转中心的距离相等
③每一点都绕着旋转中心转过相同的角度
轴对称的性质:
对应点的连线被对称轴垂直平分。
中心对称的性质:
对应点与对称中心在一条直线上,且被对称中心平分
1.如图的方格纸中,左边图形到右边图形的变换是( )
A.向右平移7格
C.绕AB的中点旋转180°,再以AB为对称轴作轴对称
D.以AB为对称轴作轴对称,再向右平移7格
B.以AB的垂直平分线为对称轴作轴对称变换,再以AB为对称轴作轴对称变换
D
当堂训练(15分钟)
2.如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10。若将△PAC绕点A逆时针旋转60°后,得到△P′AB,则点P与P′之间的距离为 ,∠APB= 。
6
150°
3.如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A'B'C'的位置后,再沿CB方向向左平移,使点B'落在原三角板ABC的斜边AB上,则三角板A'B'C'平移的距离为( )
B.4cm
A.6cm
C
D
40
4.如图2所示,△ABC绕点A逆
时针旋转某一角度得到
△ADE,
∠1=∠2=∠3=20°,则旋转角
为 度。
若
5.如图,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形。连接BG,DE。
(1)观察猜想BG与DE之间的关系,并证明你的猜想;
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由。
6.解:(1)BG⊥BD,且BG=DE。
证明:延长BG与DE交于H点,
在△BCG和△DCE中,
BC=DC
∠BCG=∠DCE=90°
CG=CE,
∴△BCG≌△DCE,
∴BG=DE,∠BGC=∠DEC,
又∵∠BGC=∠DGH,∠DEC+∠CDE=90°,
∴∠DGH+∠GDH=90°,∴∠DHG=90°,
故BG⊥DE,且BG=DE。
{
(2)存在,△BCG≌△DCE,(1)中已证明,
且△BCG和△DCE有共同顶点C,则△DCE沿C点旋转向左90°与△BCG重合。
7.含30°角的直角三角板ABC(∠B=30°)绕直角顶点C沿逆时针方向旋转角α(∠α<90°),再沿∠A的对边翻折得到△A′B′C,AB与B′C交于点M,A′B′与BC交于点N,A′B′与AB相交于点E。
(1)求证:△ACM≌△A′CN;
(2)当∠α=30°时,找出ME与MB′的数量关系,并加以说明。
7.(1)证明:∵∠A=∠A′,AC=A′C,∠ACM=∠A'CN=90°-∠MCN,
∴△ACM≌△A’CN。
(2)解:在Rt△ABC中
∵∠B=30°,∴∠A=90°-30°=60°。
又∵∠α=30°,∴∠MCN=30°,
∴∠ACM=90°-∠MCN=60°。
∴∠EMB′=∠AMC=∠A=∠MCA=60°。
∵∠B′=∠B=30°,
所以三角形MEB′是Rt△MEB′,且∠B′=30°。所以MB′=2ME。
8.如图1在四边形ABCD中。AB=AD,∠B+∠D=180゜,E、F分别是边BC、CD上的点,且∠BAD=2∠EAF。
(1)求证:EF=BE+DF;
(2)在(1)问中,若将△AEF绕点A逆时针旋转,当点E、F分别运动到BC、CD延长线上时,如图2所示,试探究EF、BE、DF之间的数量关系。
选做题
8.(1)证明:延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
BM=DF
∠ABM=∠D,
AB=AD,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
AF=AM
∠FAE=∠MAE,
AE=AE,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF。
(2)解:EF、BE、DF之间的关系是EF=BE-DF,理由是:在CB上截取BM=DF,连接AM。
∵∠ABC+∠D=180°,∠ADC+∠ADF=180°,
∴∠ABC=∠ADF,
在△ABM和△ADF中,
BM=DF,
∠B=∠ADF,
AB=AD
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF=2(∠EAD+∠DAF)=2(∠EAD+∠BAM)=∠EAF+(∠EAD+∠BAM)
又∵∠BAD=(∠BAM+∠EAD)+∠MAE
∴∠MAE=∠EAF在△FAE和△MAE中,
AF=AM
∠FAE=∠MAE,
AE=AE,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE-BM=BE-DF,
即EF=BE-DF。
9.(2012 保定一模)如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M。
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数。
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数。
9.(1)证明:∵△ABC是等边三角形
∴∠ABQ=∠CAP,AB=CA,
又∵点P、Q运动速度相同,
∴AP=BQ,
在△ABQ与△CAP中,
∴△ABQ≌△CAP(SAS)
AB=CA,
AP=BQ,
∠ABQ=∠CAP
(2)解:点P、Q在运动的过程中,∠QMC不变。
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC=∠ACP+∠MAC,
∴∠QMC=∠BAQ+∠MAC=∠BAC=60°。
选做
(3)解:点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变。
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°。
10.如图,矩形ABCD中,AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,第n次平移将矩形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向平移5个单位,得到矩形AnBnCnDn(n>2)。
(1)求AB1和AB2的长。
(2)若ABn的长为56,求n。
(1)11、16
(2)n=10
谢 谢
第三章 图形的平移与旋转 复习课件
学习目标(1分钟)
2、会利用性质作图。
3、能够综合运用平移、旋转、轴对称的性质解决实际问题。
1、巩固平移、旋转、中心对称的相关概念及基本性质;
自学指导1(1分钟)
2.平移、旋转、中心对称各有哪些性质特征?
1.平移的两要素是:__________________。
旋转的三要素是:_____________________________。
平移方向和平移距离
旋转中心、旋转方向和旋转角度
3.图形的平移与坐标变化的规律怎样?
左右平移,___坐标改变,左____,右____。
上下平移,___坐标改变,上____,下____。
如果先左(右)平移,再上(下)平移时,横、纵坐标都要改变,此时可以看成是一次平移,平移的方向是_______________________平移的距离是__________________。
横
纵
减
减
加
加
对应点的连线所在的直线
对应点的连线的长度
自学检测1(7分钟)
1.下列标志中,可以看作是中心对称图形的是( )
A.
B.
C.
D.
D
2.观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
B
3.如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )
C
D.180°
C.120°
B.90°
A.60°
5.已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为( )
C.12
D.18
B.9
A.6
D
A.把△ABC向左平移4个单位,再向下平移2个单位
B.把△ABC向右平移4个单位,再向下平移2个单位
C
4.如图,△ABC经过怎样的平移得到△DEF( )
C.把△ABC向右平移4个单位,再向上平移2个单位
D.把△ABC向左平移4个单位,再向上平移2个单位
6.如图,将一朵小花放置在平面直角坐标系第一象限内,先将它向下平移4个单位后,再将它绕原点O旋转180°,则小花顶点A的对应点A′的坐标为 。
7.在数轴上,点A向右平移1个单位,再向左平移2个单位,再向右平移3个单位,再向左平移4个单位…100次平移后A所在点表示的数为2006,则点A的原始数为 。
2056
(-3,3)
自学指导2(1分钟)
1.思考下列问题:
平移、旋转、中心对称的作图方法是什么?
平移、旋转、中心对称作图时,分别要确定哪些条件?
2.自学例题,掌握解题方法和技巧,灵活运用图形变换的基本性质解决实际问题。
例题:如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( )
A.1: B.1:2 C. :2 D.1:
B
分析:解决本题关键要突破三点:
1.△APB≌△CP/B得AP=CP/
2.△APP/是直角三角形
3.△PBP/是等腰直角三角形
自学检测2(5分钟)
1.下列说法错误的有( )
①图形在平移过程中,图形上的每一点都移动了相同的距离;
②图形在旋转过程中,图形上的每一点都绕旋转中心转过了同样长的路程;
③中心对称图形的对称中心只有1个,而轴对称图形的对称轴可能不止一条;
④等边三角形既是轴对称图形,又是中心对称图形。
A.1个
B.2个
C.3个
D.4个
B
2.如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
D.格点Q
C.格点P
B.格点N
A.点M
B
3.如图,每个小方格都是边长为1个单位长度的小正方形。
(1)将△ABC向右平移3个单位长度,画出平移后的△A1B1C1。
(2)将△ABC绕点O旋转180°,画出旋转后的△A2B2C2。(3)画出一条直线将△AC1A2的面积分成相等的两部分。
5.如图2所示,在平面内将Rt△ABC绕直角顶点C逆
时针旋转90°得到Rt△EFC。若AB=
BE的长为 。
,BC=1,则线段
3
4.如图1,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转一定的角度后能与△CBP′重合。若PB=3,则PP′= 。
图1 P′
图2
(2013 黄石) 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
C.4
B.5
B
解决此题关键是判断出△ACO是等腰直角三角形。
先求出∠ACD=30°,再根据旋转角求出∠ACD1=45°。
讨论、更正、点拨(4分钟)
点拨:
本题用到重要的知识点:1.旋转的性质,2.勾股定理,3.直角三角形中斜边上的中线等于斜边的一半。
一、考点:
1.平移、旋转、对称的基本性质
2.网格作图
3.基本性质的应用
二、难点:
1.旋转作图
2.图形的旋转与证明
三、易错、易漏点:
1.中心对称与中心对称图形的概念
2.旋转作图
3.中心对称与轴对称
4.图形的平移与坐标变化关系
5.旋转具有三要素,缺一不可
平移的基本性质:
①对应线段平行且相等;
②对应角相等
③对应点的连线平行 且相等
旋转的基本性质:
①对应线段相等,对应角相等
②对应点到旋转中心的距离相等
③每一点都绕着旋转中心转过相同的角度
轴对称的性质:
对应点的连线被对称轴垂直平分。
中心对称的性质:
对应点与对称中心在一条直线上,且被对称中心平分
1.如图的方格纸中,左边图形到右边图形的变换是( )
A.向右平移7格
C.绕AB的中点旋转180°,再以AB为对称轴作轴对称
D.以AB为对称轴作轴对称,再向右平移7格
B.以AB的垂直平分线为对称轴作轴对称变换,再以AB为对称轴作轴对称变换
D
当堂训练(15分钟)
2.如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10。若将△PAC绕点A逆时针旋转60°后,得到△P′AB,则点P与P′之间的距离为 ,∠APB= 。
6
150°
3.如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A'B'C'的位置后,再沿CB方向向左平移,使点B'落在原三角板ABC的斜边AB上,则三角板A'B'C'平移的距离为( )
B.4cm
A.6cm
C
D
40
4.如图2所示,△ABC绕点A逆
时针旋转某一角度得到
△ADE,
∠1=∠2=∠3=20°,则旋转角
为 度。
若
5.如图,B,C,E是同一直线上的三个点,四边形ABCD与四边形CEFG都是正方形。连接BG,DE。
(1)观察猜想BG与DE之间的关系,并证明你的猜想;
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由。
6.解:(1)BG⊥BD,且BG=DE。
证明:延长BG与DE交于H点,
在△BCG和△DCE中,
BC=DC
∠BCG=∠DCE=90°
CG=CE,
∴△BCG≌△DCE,
∴BG=DE,∠BGC=∠DEC,
又∵∠BGC=∠DGH,∠DEC+∠CDE=90°,
∴∠DGH+∠GDH=90°,∴∠DHG=90°,
故BG⊥DE,且BG=DE。
{
(2)存在,△BCG≌△DCE,(1)中已证明,
且△BCG和△DCE有共同顶点C,则△DCE沿C点旋转向左90°与△BCG重合。
7.含30°角的直角三角板ABC(∠B=30°)绕直角顶点C沿逆时针方向旋转角α(∠α<90°),再沿∠A的对边翻折得到△A′B′C,AB与B′C交于点M,A′B′与BC交于点N,A′B′与AB相交于点E。
(1)求证:△ACM≌△A′CN;
(2)当∠α=30°时,找出ME与MB′的数量关系,并加以说明。
7.(1)证明:∵∠A=∠A′,AC=A′C,∠ACM=∠A'CN=90°-∠MCN,
∴△ACM≌△A’CN。
(2)解:在Rt△ABC中
∵∠B=30°,∴∠A=90°-30°=60°。
又∵∠α=30°,∴∠MCN=30°,
∴∠ACM=90°-∠MCN=60°。
∴∠EMB′=∠AMC=∠A=∠MCA=60°。
∵∠B′=∠B=30°,
所以三角形MEB′是Rt△MEB′,且∠B′=30°。所以MB′=2ME。
8.如图1在四边形ABCD中。AB=AD,∠B+∠D=180゜,E、F分别是边BC、CD上的点,且∠BAD=2∠EAF。
(1)求证:EF=BE+DF;
(2)在(1)问中,若将△AEF绕点A逆时针旋转,当点E、F分别运动到BC、CD延长线上时,如图2所示,试探究EF、BE、DF之间的数量关系。
选做题
8.(1)证明:延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
BM=DF
∠ABM=∠D,
AB=AD,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
AF=AM
∠FAE=∠MAE,
AE=AE,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF。
(2)解:EF、BE、DF之间的关系是EF=BE-DF,理由是:在CB上截取BM=DF,连接AM。
∵∠ABC+∠D=180°,∠ADC+∠ADF=180°,
∴∠ABC=∠ADF,
在△ABM和△ADF中,
BM=DF,
∠B=∠ADF,
AB=AD
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF=2(∠EAD+∠DAF)=2(∠EAD+∠BAM)=∠EAF+(∠EAD+∠BAM)
又∵∠BAD=(∠BAM+∠EAD)+∠MAE
∴∠MAE=∠EAF在△FAE和△MAE中,
AF=AM
∠FAE=∠MAE,
AE=AE,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE-BM=BE-DF,
即EF=BE-DF。
9.(2012 保定一模)如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M。
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数。
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数。
9.(1)证明:∵△ABC是等边三角形
∴∠ABQ=∠CAP,AB=CA,
又∵点P、Q运动速度相同,
∴AP=BQ,
在△ABQ与△CAP中,
∴△ABQ≌△CAP(SAS)
AB=CA,
AP=BQ,
∠ABQ=∠CAP
(2)解:点P、Q在运动的过程中,∠QMC不变。
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC=∠ACP+∠MAC,
∴∠QMC=∠BAQ+∠MAC=∠BAC=60°。
选做
(3)解:点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变。
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°。
10.如图,矩形ABCD中,AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,第n次平移将矩形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向平移5个单位,得到矩形AnBnCnDn(n>2)。
(1)求AB1和AB2的长。
(2)若ABn的长为56,求n。
(1)11、16
(2)n=10
谢 谢
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
