1.5.2 平方差公式的应用 基础训练(含解析)
文档属性
| 名称 | 1.5.2 平方差公式的应用 基础训练(含解析) | 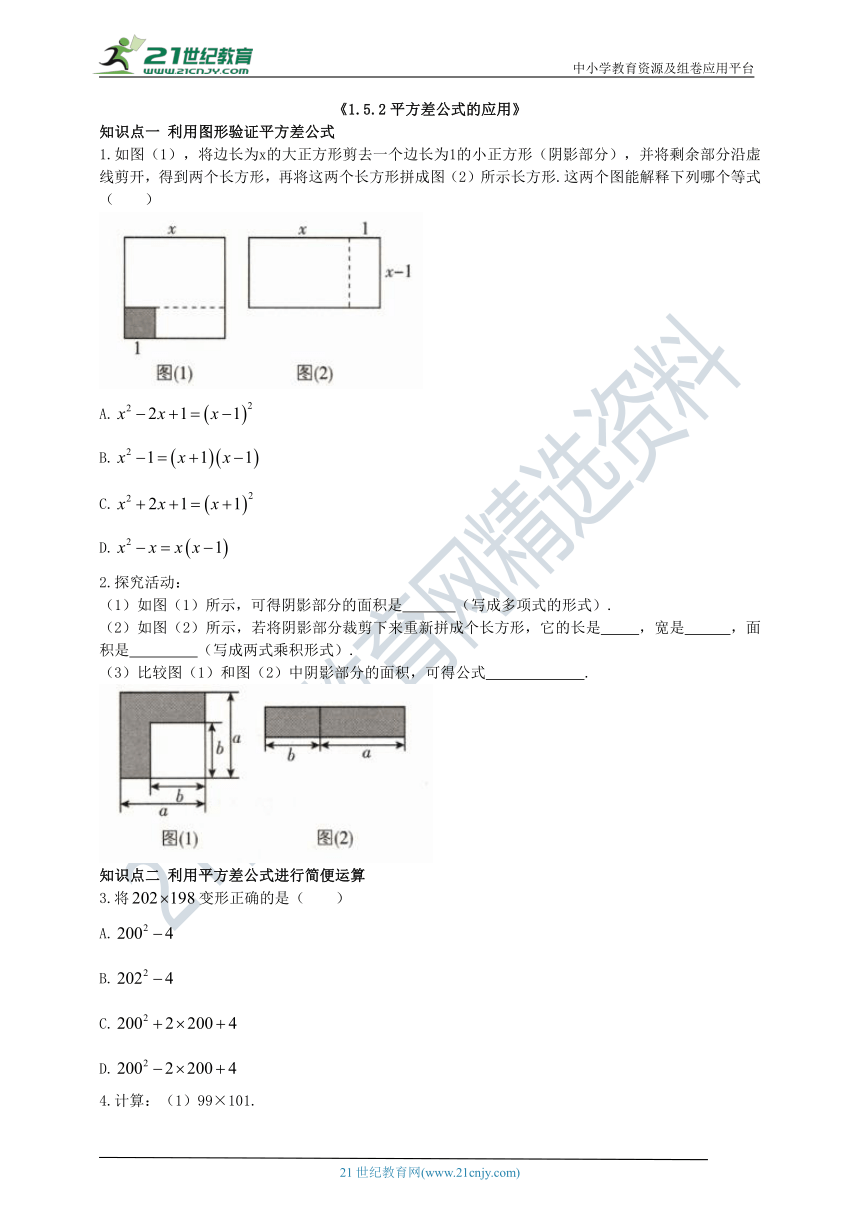 | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 21:41:53 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《1.5.2平方差公式的应用》
知识点一 利用图形验证平方差公式
1.如图(1),将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图(2)所示长方形.这两个图能解释下列哪个等式( )
A.
B.
C.
D.
2.探究活动:
(1)如图(1)所示,可得阴影部分的面积是 (写成多项式的形式).
(2)如图(2)所示,若将阴影部分裁剪下来重新拼成个长方形,它的长是 ,宽是 ,面积是 (写成两式乘积形式).
(3)比较图(1)和图(2)中阴影部分的面积,可得公式 .
知识点二 利用平方差公式进行简便运算
3.将变形正确的是( )
A.
B.
C.
D.
4.计算:(1)99×101.
(2)
(3)
知识点三 平方差公式的实际应用
5.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3 m,东西方向缩短3 m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A.增加6
B.增加9
C.减少9
D.保持不变
6.如图,小刚家有一块L形菜地,要把L形菜地按如图所示的方式分成面积相等的两个梯形,种上不同的蔬菜.这两个梯形的上底都是米,下底都是米,高都是米.
(1)小刚家的菜地面积是多少平方米?
(2)当=20米,=30米时,菜地的面积是多少?
参考答案
1.答案:B
解析:由题图可知,题图(1)空白部分的面积为,题图(2)的面积为,所以.故选B.
2.答案:(1)(2) (3)
解析:(1)阴影部分的面积为.故答案为.
(2)将阴影部分裁剪下来重新拼成一个长方形,它的长是,宽是,面积是.故答案为
(3)
3.答案:A
解析:故选A.
4.答案:(1)
(2)
(3)
5.答案:C
解析:设改造前正方形草坪的边长为m,则面积为.将正方形草坪的南北方向增加3m,东西方向缩短3m后,草坪的长为m,宽为m,面积为
.故改造后面积减少9.故选C.
6.答案:(1)由题意得,菜地的面积为平方米.故小刚家的菜地面积是平方米.
(2)当=20米,=30米时,原式==500(平方米).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
《1.5.2平方差公式的应用》
知识点一 利用图形验证平方差公式
1.如图(1),将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图(2)所示长方形.这两个图能解释下列哪个等式( )
A.
B.
C.
D.
2.探究活动:
(1)如图(1)所示,可得阴影部分的面积是 (写成多项式的形式).
(2)如图(2)所示,若将阴影部分裁剪下来重新拼成个长方形,它的长是 ,宽是 ,面积是 (写成两式乘积形式).
(3)比较图(1)和图(2)中阴影部分的面积,可得公式 .
知识点二 利用平方差公式进行简便运算
3.将变形正确的是( )
A.
B.
C.
D.
4.计算:(1)99×101.
(2)
(3)
知识点三 平方差公式的实际应用
5.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3 m,东西方向缩短3 m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )
A.增加6
B.增加9
C.减少9
D.保持不变
6.如图,小刚家有一块L形菜地,要把L形菜地按如图所示的方式分成面积相等的两个梯形,种上不同的蔬菜.这两个梯形的上底都是米,下底都是米,高都是米.
(1)小刚家的菜地面积是多少平方米?
(2)当=20米,=30米时,菜地的面积是多少?
参考答案
1.答案:B
解析:由题图可知,题图(1)空白部分的面积为,题图(2)的面积为,所以.故选B.
2.答案:(1)(2) (3)
解析:(1)阴影部分的面积为.故答案为.
(2)将阴影部分裁剪下来重新拼成一个长方形,它的长是,宽是,面积是.故答案为
(3)
3.答案:A
解析:故选A.
4.答案:(1)
(2)
(3)
5.答案:C
解析:设改造前正方形草坪的边长为m,则面积为.将正方形草坪的南北方向增加3m,东西方向缩短3m后,草坪的长为m,宽为m,面积为
.故改造后面积减少9.故选C.
6.答案:(1)由题意得,菜地的面积为平方米.故小刚家的菜地面积是平方米.
(2)当=20米,=30米时,原式==500(平方米).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
