苏科版七年级数学下册12.2证明(3) 课件(共18张PPT)
文档属性
| 名称 | 苏科版七年级数学下册12.2证明(3) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 23:27:14 | ||
图片预览






文档简介
(共18张PPT)
12.2 证明
通过上节课的学习,我们知道直观判断有时是不可靠的.
一个数学结论的正确性如何证实呢
?
引入
欧几里得
其实数学家们早就遇到了这样的问题,人类对数学命题进行证明的研究已有2000多年的历史了,公元前3世纪,古希腊数学家欧几里得写出了举世闻名的巨著《原本》,在这本书中,他挑选了一些基本定义和基本事实作为证实其他命题的出发点,推导出400多条定理.《原本》是人类智慧的伟大成就之一,它对科学和人类文化的发展产生了深远的影响.
阅读
初一几何我们学过的基本事实(即公理)有:
基本事实
①经过两点有一条直线,并且只有一条直线.
②经过直线外一点有且只有一条直线与这条直线平行.
③同位角相等,两直线平行.
④两直线平行,同位角相等.
下面,让我们追寻欧几里得的足迹,通过从基本事实出发证明“垂直于同一条直线的两条直线平行”
根据已知的真命题,确定某个命题真实性的过程叫做证明。
经过证明的真命题称为定理。
本节课我们提供的推理依据是:两直线平行,同位角相等;同位角相等,两直线平行。还有等量代换,等式性质,不等式性质。基本定义是我们课本上已学过的定义。
探索活动
垂直于同一条直线的两条直线平行
1、这个命题的条件是什么?结论是什么?
2、你能根据命题的条件画出相应的图形吗?
3、你能结合所画的图形写出已知和求证吗?
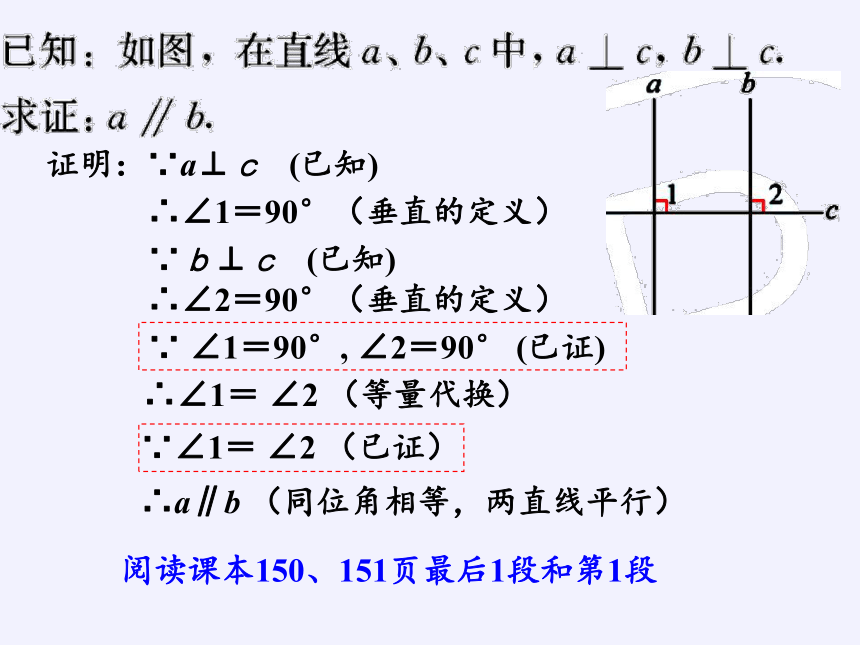
证明:∵a⊥c (已知)
∴∠1=90°(垂直的定义)
∵b⊥c (已知)
∴∠2=90°(垂直的定义)
∵ ∠1=90°, ∠2=90° (已证)
∴∠1= ∠2 (等量代换)
∵∠1= ∠2 (已证)
∴a∥b (同位角相等,两直线平行)
阅读课本150、151页最后1段和第1段
证明与图形有关的命题,一般有以下步骤:
1.根据题意,画出图形;
2.根据命题的条件、结论,结合图形,写出已知、求证;
3.写出证明过程.
归纳小结
两条平行线被第三条直线所截,一组同位角的角平分线互相平行.
例题精讲
依据基本事实“同位角相等,两直线平行”来证.
见课本151页证明过程
已知:A、O、B在一直线上,OM
平分 AOC,ON平分 BOC,
求证:OM ON
A
O
B
C
M
N
1
2
巩固练习
A
O
B
C
M
N
1
2
证明: ∵OM平分 AOC( )
∴ 1= AOC( )
∵ ON平分 BOC( )
∴ 2= BOC( )
∴ 1+ 2= AOC+ BOC= AOB ( )
∵ A、O、B在一直线上( )
所以 AOB=180( )
所以 1+ 2= 180 = 90( )
所以OM ON( )
已知
角平分线定义
已知
角平分线定义
等式性质
已知
平角定义
等量代换
垂直定义
例题精讲
内错角相等,两直线平行
同位角相等,两直线平行
活学活用
同旁内角互补,两直线平行
AD BC
活学活用
AB CD
AD BC
活学活用
已知
1
3
2
4
内错角相等,两直线平行
证明------用推理的方法证实真命题的过程.
推理------
因为A
所以B (事实依据)
事实依据------
基本事实(公理)
定义
定理
等式或不等式的性质
言之有理,步步有据,过程严谨, 结论求实.
回顾反思
+已知条件
谢 谢
12.2 证明
通过上节课的学习,我们知道直观判断有时是不可靠的.
一个数学结论的正确性如何证实呢
?
引入
欧几里得
其实数学家们早就遇到了这样的问题,人类对数学命题进行证明的研究已有2000多年的历史了,公元前3世纪,古希腊数学家欧几里得写出了举世闻名的巨著《原本》,在这本书中,他挑选了一些基本定义和基本事实作为证实其他命题的出发点,推导出400多条定理.《原本》是人类智慧的伟大成就之一,它对科学和人类文化的发展产生了深远的影响.
阅读
初一几何我们学过的基本事实(即公理)有:
基本事实
①经过两点有一条直线,并且只有一条直线.
②经过直线外一点有且只有一条直线与这条直线平行.
③同位角相等,两直线平行.
④两直线平行,同位角相等.
下面,让我们追寻欧几里得的足迹,通过从基本事实出发证明“垂直于同一条直线的两条直线平行”
根据已知的真命题,确定某个命题真实性的过程叫做证明。
经过证明的真命题称为定理。
本节课我们提供的推理依据是:两直线平行,同位角相等;同位角相等,两直线平行。还有等量代换,等式性质,不等式性质。基本定义是我们课本上已学过的定义。
探索活动
垂直于同一条直线的两条直线平行
1、这个命题的条件是什么?结论是什么?
2、你能根据命题的条件画出相应的图形吗?
3、你能结合所画的图形写出已知和求证吗?
证明:∵a⊥c (已知)
∴∠1=90°(垂直的定义)
∵b⊥c (已知)
∴∠2=90°(垂直的定义)
∵ ∠1=90°, ∠2=90° (已证)
∴∠1= ∠2 (等量代换)
∵∠1= ∠2 (已证)
∴a∥b (同位角相等,两直线平行)
阅读课本150、151页最后1段和第1段
证明与图形有关的命题,一般有以下步骤:
1.根据题意,画出图形;
2.根据命题的条件、结论,结合图形,写出已知、求证;
3.写出证明过程.
归纳小结
两条平行线被第三条直线所截,一组同位角的角平分线互相平行.
例题精讲
依据基本事实“同位角相等,两直线平行”来证.
见课本151页证明过程
已知:A、O、B在一直线上,OM
平分 AOC,ON平分 BOC,
求证:OM ON
A
O
B
C
M
N
1
2
巩固练习
A
O
B
C
M
N
1
2
证明: ∵OM平分 AOC( )
∴ 1= AOC( )
∵ ON平分 BOC( )
∴ 2= BOC( )
∴ 1+ 2= AOC+ BOC= AOB ( )
∵ A、O、B在一直线上( )
所以 AOB=180( )
所以 1+ 2= 180 = 90( )
所以OM ON( )
已知
角平分线定义
已知
角平分线定义
等式性质
已知
平角定义
等量代换
垂直定义
例题精讲
内错角相等,两直线平行
同位角相等,两直线平行
活学活用
同旁内角互补,两直线平行
AD BC
活学活用
AB CD
AD BC
活学活用
已知
1
3
2
4
内错角相等,两直线平行
证明------用推理的方法证实真命题的过程.
推理------
因为A
所以B (事实依据)
事实依据------
基本事实(公理)
定义
定理
等式或不等式的性质
言之有理,步步有据,过程严谨, 结论求实.
回顾反思
+已知条件
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
