1.1.1 等腰三角形的性质 基础训练(含解析)
文档属性
| 名称 | 1.1.1 等腰三角形的性质 基础训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 21:51:01 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
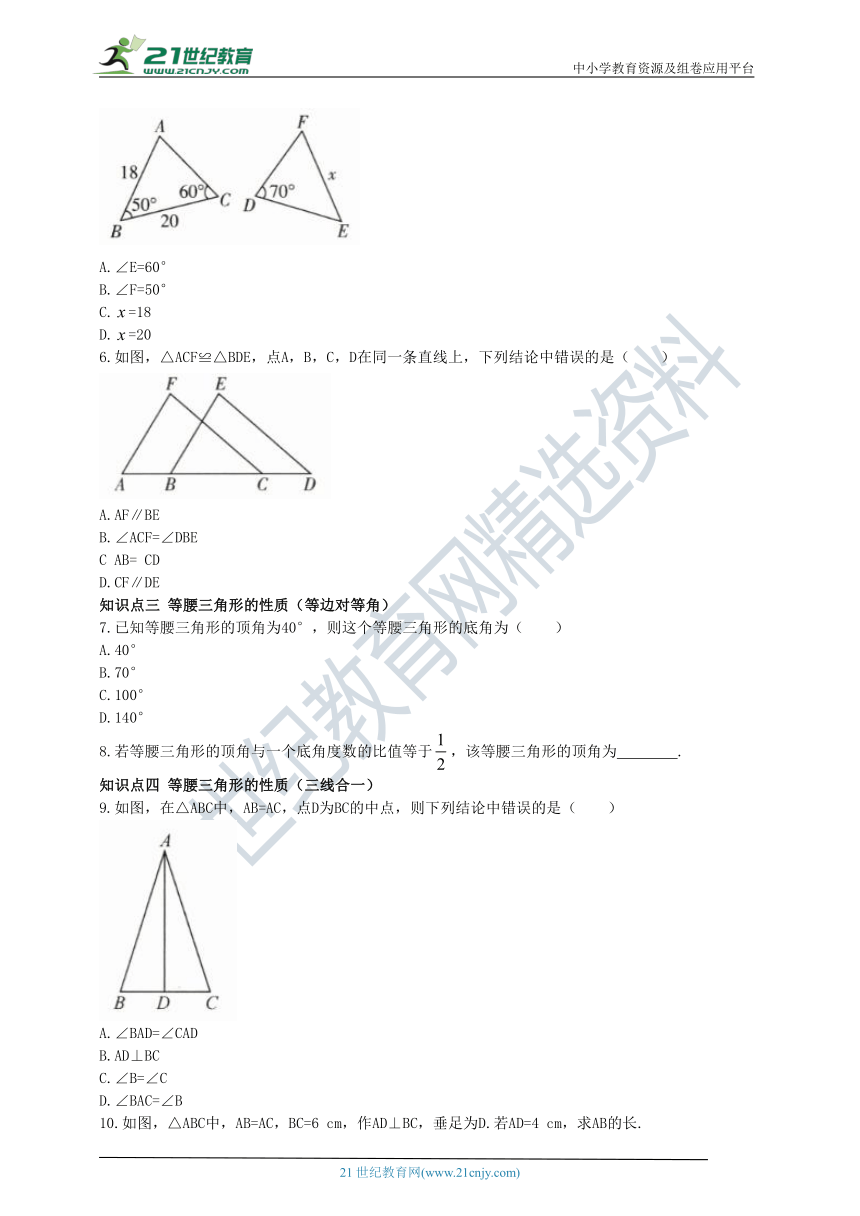
《1.1.1等腰三角形的性质》
知识点一 全等三角形的判定
1.下列条件中不能判定两个三角形全等的是( )
A. SSA
B. SAS
C. ASA
D. AAS
2.下列各图中,分别为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
3.如图,AB=DE,∠A=∠D,那么要得到△ABC≌△DEF,可以添加一个条件是
,△ABC与△DEF全等的理由是 .
4.如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.
知识点二 全等三角形的性质
5.如图,△ABC≌△DEF,则下列结论正确的是( )
A.∠E=60°
B.∠F=50°
C.=18
D.=20
6.如图,△ACF≌△BDE,点A,B,C,D在同一条直线上,下列结论中错误的是( )
A.AF∥BE
B.∠ACF=∠DBE
C AB= CD
D.CF∥DE
知识点三 等腰三角形的性质(等边对等角)
7.已知等腰三角形的顶角为40°,则这个等腰三角形的底角为( )
A.40°
B.70°
C.100°
D.140°
8.若等腰三角形的顶角与一个底角度数的比值等于,该等腰三角形的顶角为 .
知识点四 等腰三角形的性质(三线合一)
9.如图,在△ABC中,AB=AC,点D为BC的中点,则下列结论中错误的是( )
A.∠BAD=∠CAD
B.AD⊥BC
C.∠B=∠C
D.∠BAC=∠B
10.如图,△ABC中,AB=AC,BC=6 cm,作AD⊥BC,垂足为D.若AD=4 cm,求AB的长.
易错点 已知等腰三角形的一个内角,求另外两个内角时,未分类讨论致错
11.等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55°
B.70°,40°或70°,55°
C.70°,40°
D.55°,55°或70°,40°
参考答案
1.答案:A
解析:SAS,ASA,AAS可以判定两个三角形全等,SSA不能判定两个三角形全等.故选A.
2.答案:B
解析:在△ABC和三角形乙中,满足SAS,所以三角形乙和△ABC全等;在△ABC和三角形丙中,满足AAS,所以三角形丙和△ABC全等;不能判定甲与△ABC全等.故选B.
3. 答案:(答案不唯一)AC=DF SAS
解析:△ABC与△DEF的已知一边一角对应相等,根据SAS添加一组边对应相等,或根据ASA,AAS添加一组角对应相等可得△ABC≌△DEF.
4.答案:∵在和中,∴
解析:
5.答案:D
解析:∵△ABC≌△DEF,∴∠E=∠B=50°,A错误;∵△ABC≌△DEF,∴∠F=∠C=60°,B错误;EF=BC=20,即=20,C错误、D正确.故选D.
6.答案:B
解析:∵△ACF≌△BDE,,∴∠A=∠EBD,∴AF∥BE,A正确,不符合题意;∴∠ACF=∠BDE,B错误;符合题意;∴AC=BD,∴AB=CD,C正确,不符合题意;∴∠D=∠FCA,∴CF∥DE,D正确,不符合题意.故选B.
7.答案:B
解析:∵等腰三角形的顶角为40°,∴这个等腰三角形的底角为(180°-40°)÷2=70°故选B.
8.答案:36°
解析:设在△ABC中,AB=AC,∴∠B=∠C.∵顶角与一个底角度数的比值等于,∴∠A:∠B:∠C=1:2:2,即5∠A=180°,∴∠A=36°.故答案为36°.
9.答案:D
解析:在△ABC中,AB=AC,点D为BC的中点,根据等边对等角与等腰三角形三线合一的性质,可得∠B=∠C,∠BAD=∠CAD,AD⊥BC.故选D.
10.答案:∵AB=AC,BC=6 cm,AD⊥BC,∴.BD=BC=3 cm.∵AD=4cm,∴AB==5(cm).
解析:
11.答案:D
解析:分情况讨论:
(1)若等腰三角形的顶角为70°时,底角为(180°-70°)÷2=55°;
(2)若等腰三角形的底角为70°时,它的另外一个底角为70°,顶角为180°-70°-70°=40°.故选D.
易错警示已知给出了等腰三角形的一个内角是70°,没有明确是顶角还是底角,所以要进行分类讨论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
《1.1.1等腰三角形的性质》
知识点一 全等三角形的判定
1.下列条件中不能判定两个三角形全等的是( )
A. SSA
B. SAS
C. ASA
D. AAS
2.下列各图中,分别为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
3.如图,AB=DE,∠A=∠D,那么要得到△ABC≌△DEF,可以添加一个条件是
,△ABC与△DEF全等的理由是 .
4.如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.
知识点二 全等三角形的性质
5.如图,△ABC≌△DEF,则下列结论正确的是( )
A.∠E=60°
B.∠F=50°
C.=18
D.=20
6.如图,△ACF≌△BDE,点A,B,C,D在同一条直线上,下列结论中错误的是( )
A.AF∥BE
B.∠ACF=∠DBE
C AB= CD
D.CF∥DE
知识点三 等腰三角形的性质(等边对等角)
7.已知等腰三角形的顶角为40°,则这个等腰三角形的底角为( )
A.40°
B.70°
C.100°
D.140°
8.若等腰三角形的顶角与一个底角度数的比值等于,该等腰三角形的顶角为 .
知识点四 等腰三角形的性质(三线合一)
9.如图,在△ABC中,AB=AC,点D为BC的中点,则下列结论中错误的是( )
A.∠BAD=∠CAD
B.AD⊥BC
C.∠B=∠C
D.∠BAC=∠B
10.如图,△ABC中,AB=AC,BC=6 cm,作AD⊥BC,垂足为D.若AD=4 cm,求AB的长.
易错点 已知等腰三角形的一个内角,求另外两个内角时,未分类讨论致错
11.等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55°
B.70°,40°或70°,55°
C.70°,40°
D.55°,55°或70°,40°
参考答案
1.答案:A
解析:SAS,ASA,AAS可以判定两个三角形全等,SSA不能判定两个三角形全等.故选A.
2.答案:B
解析:在△ABC和三角形乙中,满足SAS,所以三角形乙和△ABC全等;在△ABC和三角形丙中,满足AAS,所以三角形丙和△ABC全等;不能判定甲与△ABC全等.故选B.
3. 答案:(答案不唯一)AC=DF SAS
解析:△ABC与△DEF的已知一边一角对应相等,根据SAS添加一组边对应相等,或根据ASA,AAS添加一组角对应相等可得△ABC≌△DEF.
4.答案:∵在和中,∴
解析:
5.答案:D
解析:∵△ABC≌△DEF,∴∠E=∠B=50°,A错误;∵△ABC≌△DEF,∴∠F=∠C=60°,B错误;EF=BC=20,即=20,C错误、D正确.故选D.
6.答案:B
解析:∵△ACF≌△BDE,,∴∠A=∠EBD,∴AF∥BE,A正确,不符合题意;∴∠ACF=∠BDE,B错误;符合题意;∴AC=BD,∴AB=CD,C正确,不符合题意;∴∠D=∠FCA,∴CF∥DE,D正确,不符合题意.故选B.
7.答案:B
解析:∵等腰三角形的顶角为40°,∴这个等腰三角形的底角为(180°-40°)÷2=70°故选B.
8.答案:36°
解析:设在△ABC中,AB=AC,∴∠B=∠C.∵顶角与一个底角度数的比值等于,∴∠A:∠B:∠C=1:2:2,即5∠A=180°,∴∠A=36°.故答案为36°.
9.答案:D
解析:在△ABC中,AB=AC,点D为BC的中点,根据等边对等角与等腰三角形三线合一的性质,可得∠B=∠C,∠BAD=∠CAD,AD⊥BC.故选D.
10.答案:∵AB=AC,BC=6 cm,AD⊥BC,∴.BD=BC=3 cm.∵AD=4cm,∴AB==5(cm).
解析:
11.答案:D
解析:分情况讨论:
(1)若等腰三角形的顶角为70°时,底角为(180°-70°)÷2=55°;
(2)若等腰三角形的底角为70°时,它的另外一个底角为70°,顶角为180°-70°-70°=40°.故选D.
易错警示已知给出了等腰三角形的一个内角是70°,没有明确是顶角还是底角,所以要进行分类讨论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
