1.1.4_等边三角形的判定 基础训练(含答案)
文档属性
| 名称 | 1.1.4_等边三角形的判定 基础训练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 21:39:40 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
《1.1.4等边二角形的判定》
知识点一 等边三角形的判定
1.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③④
B.①②④
C.①③
D.②③④
2.若△ABC的三条边长分别是,且=0,则这个三角形是( )
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
3.如图,AB=AC,∠BAC=120°,AD⊥AC,AE⊥AB.求证:△ADE是等边三角形.
4.如图,在△ABC中,∠A=120°,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,点E,F为垂足,求证:△DEF是等边三角形.
知识点二 含30°角的直角三角形的性质
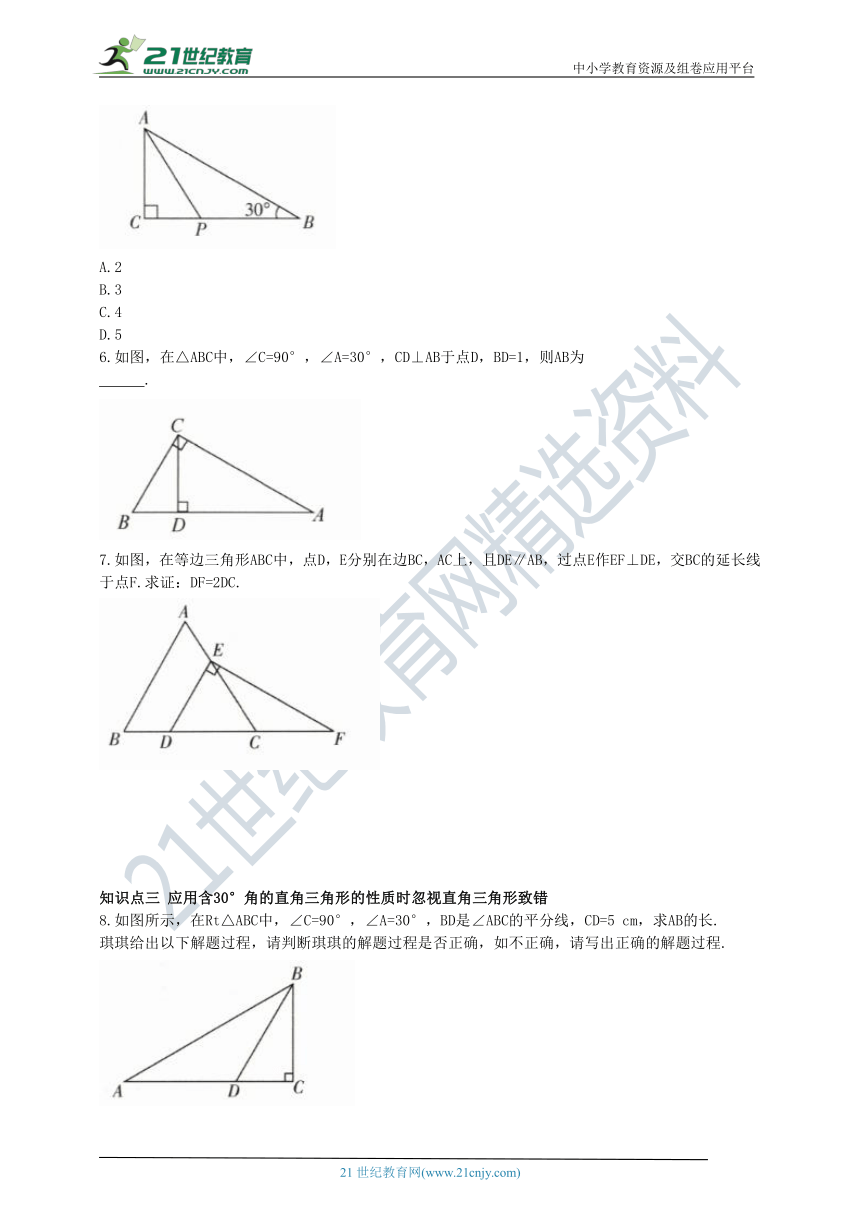
5.如图,在△ABC中,∠C=90°,AC=2,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是( )
A.2
B.3
C.4
D.5
6.如图,在△ABC中,∠C=90°,∠A=30°,CD⊥AB于点D,BD=1,则AB为
.
7.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.求证:DF=2DC.
知识点三 应用含30°角的直角三角形的性质时忽视直角三角形致错
8.如图所示,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5 cm,求AB的长.
琪琪给出以下解题过程,请判断琪琪的解题过程是否正确,如不正确,请写出正确的解题过程.
解:∵∠C=90°,∠A=30°,∴∠ABC=180°-∠A-∠C=60°.∵BD是∠ABC的平分线,∴∠CBD=∠ABC=30°,即在Rt△BCD中,∠CBD=30°,∴BD=2CD=10 cm,∴AB=20 cm.
参考答案
1.答案:A
解析:①有两个角等于60°,则第三个角也是60°,则其是等边三角形;②有一个角等于60°的等腰三角形是等边三角形;③三个外角相等,则三个内角相等,则其是等边三角形;④由题意可得该等腰三角形的腰与底边相等,则三角形三边相等,则其是等边三角形.所以都正确.故选A.
2.答案:B
解析:∵=0,∴=0且=0,∴,∴△ABC为等边三角形.故选B.
3.答案:【证明】在△ABC中,∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.∵AD⊥AC,AE⊥AB,∴∠ADC=∠AEB=∠DAE=60°,∴△ADE是等边三角形.
解析:
4.答案:【证明】∵∠A=120°,AB=AC,∴∠B=∠C=30°.又∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°,∴∠BDE=∠CDF=60°,∴∠EDF=60°.∵D是BC的中点,∴BD=CD.在△BDE与△CDF中,∴△BDE≌△CDF,∴DE=DF∴△DEF是等边三角形.
解析:
5.答案:D
解析:根据垂线段最短,可知AP的长不可能小于2.∵△ABC中,∠C=90°,AC=2,∠B=30°,∴AB=4,∴AP的长不可能大于4.故选D.
6.答案:4
解析:∵∠A=30°,∠BCA=90°,∴∠B=60°.∵CD⊥AB,∴∠BCD=30°,∴BC=2BD=2,∴AB=2BC=4.
7.答案:【证明】∵△ABC是等边三角形,∴∠B=60°.∵DE∥AB,∴∠EDC=∠B=60°.∵EF⊥DE,∴∠DEF=90°,∴∠F=90°-∠EDC=30°.∵∠ACB=60°,∠EDC=60°,∴△EDC是等边三角形,∴ED=DC.∵∠DEF=90°,∠F=30°,∴DF=2DE=2DC.
解析:
8.答案:【解】琪琪的解题过程不正确.正确的解题过程如下:
∵∠C=90°,∠A=30°,∴∠ABC=180°-∠A-∠C=60°.∵BD是∠ABC的平分线,∴∠CBD=∠ABC=30°,即在Rt△BCD中,∠CBD=30°,∴BD=2CD=10 cm(含30°角的直角三角形的性质)由勾股定理,得BC= cm.∵∠A=30°,∠C=90°,∴AB=2BC= cm.
解析:易错警示 含30°角的直角三角形的性质,前提条件是在直角三角形中,其次就是要找准30°角所对的直角边和斜边.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
《1.1.4等边二角形的判定》
知识点一 等边三角形的判定
1.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③④
B.①②④
C.①③
D.②③④
2.若△ABC的三条边长分别是,且=0,则这个三角形是( )
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
3.如图,AB=AC,∠BAC=120°,AD⊥AC,AE⊥AB.求证:△ADE是等边三角形.
4.如图,在△ABC中,∠A=120°,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,点E,F为垂足,求证:△DEF是等边三角形.
知识点二 含30°角的直角三角形的性质
5.如图,在△ABC中,∠C=90°,AC=2,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是( )
A.2
B.3
C.4
D.5
6.如图,在△ABC中,∠C=90°,∠A=30°,CD⊥AB于点D,BD=1,则AB为
.
7.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.求证:DF=2DC.
知识点三 应用含30°角的直角三角形的性质时忽视直角三角形致错
8.如图所示,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5 cm,求AB的长.
琪琪给出以下解题过程,请判断琪琪的解题过程是否正确,如不正确,请写出正确的解题过程.
解:∵∠C=90°,∠A=30°,∴∠ABC=180°-∠A-∠C=60°.∵BD是∠ABC的平分线,∴∠CBD=∠ABC=30°,即在Rt△BCD中,∠CBD=30°,∴BD=2CD=10 cm,∴AB=20 cm.
参考答案
1.答案:A
解析:①有两个角等于60°,则第三个角也是60°,则其是等边三角形;②有一个角等于60°的等腰三角形是等边三角形;③三个外角相等,则三个内角相等,则其是等边三角形;④由题意可得该等腰三角形的腰与底边相等,则三角形三边相等,则其是等边三角形.所以都正确.故选A.
2.答案:B
解析:∵=0,∴=0且=0,∴,∴△ABC为等边三角形.故选B.
3.答案:【证明】在△ABC中,∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.∵AD⊥AC,AE⊥AB,∴∠ADC=∠AEB=∠DAE=60°,∴△ADE是等边三角形.
解析:
4.答案:【证明】∵∠A=120°,AB=AC,∴∠B=∠C=30°.又∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°,∴∠BDE=∠CDF=60°,∴∠EDF=60°.∵D是BC的中点,∴BD=CD.在△BDE与△CDF中,∴△BDE≌△CDF,∴DE=DF∴△DEF是等边三角形.
解析:
5.答案:D
解析:根据垂线段最短,可知AP的长不可能小于2.∵△ABC中,∠C=90°,AC=2,∠B=30°,∴AB=4,∴AP的长不可能大于4.故选D.
6.答案:4
解析:∵∠A=30°,∠BCA=90°,∴∠B=60°.∵CD⊥AB,∴∠BCD=30°,∴BC=2BD=2,∴AB=2BC=4.
7.答案:【证明】∵△ABC是等边三角形,∴∠B=60°.∵DE∥AB,∴∠EDC=∠B=60°.∵EF⊥DE,∴∠DEF=90°,∴∠F=90°-∠EDC=30°.∵∠ACB=60°,∠EDC=60°,∴△EDC是等边三角形,∴ED=DC.∵∠DEF=90°,∠F=30°,∴DF=2DE=2DC.
解析:
8.答案:【解】琪琪的解题过程不正确.正确的解题过程如下:
∵∠C=90°,∠A=30°,∴∠ABC=180°-∠A-∠C=60°.∵BD是∠ABC的平分线,∴∠CBD=∠ABC=30°,即在Rt△BCD中,∠CBD=30°,∴BD=2CD=10 cm(含30°角的直角三角形的性质)由勾股定理,得BC= cm.∵∠A=30°,∠C=90°,∴AB=2BC= cm.
解析:易错警示 含30°角的直角三角形的性质,前提条件是在直角三角形中,其次就是要找准30°角所对的直角边和斜边.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
