1.1.2 等边三角形的性质 基础训练(含解析)
文档属性
| 名称 | 1.1.2 等边三角形的性质 基础训练(含解析) | 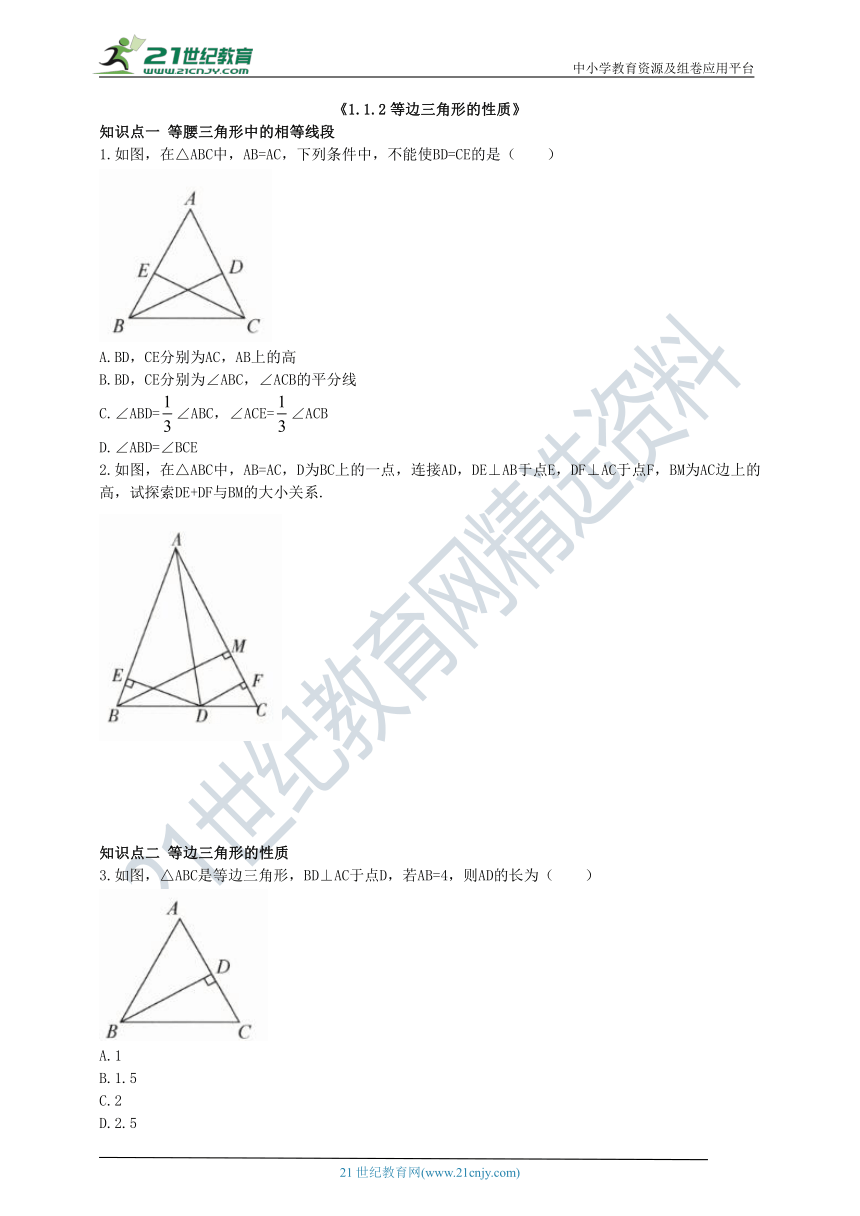 | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 21:48:23 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《1.1.2等边三角形的性质》
知识点一 等腰三角形中的相等线段
1.如图,在△ABC中,AB=AC,下列条件中,不能使BD=CE的是( )
A.BD,CE分别为AC,AB上的高
B.BD,CE分别为∠ABC,∠ACB的平分线
C.∠ABD=∠ABC,∠ACE=∠ACB
D.∠ABD=∠BCE
2.如图,在△ABC中,AB=AC,D为BC上的一点,连接AD,DE⊥AB于点E,DF⊥AC于点F,BM为AC边上的高,试探索DE+DF与BM的大小关系.
知识点二 等边三角形的性质
3.如图,△ABC是等边三角形,BD⊥AC于点D,若AB=4,则AD的长为( )
A.1
B.1.5
C.2
D.2.5
4.等边三角形的边长为2,则该等边三角形的面积是( )
A.
B.2
C.1
D.
5.三个等边三角形的摆放位置如图所示,若∠1+∠2=120°,则∠3的度数为( )
A.90°
B.60°
C.45°
D.30°
6.如图,△ABC是等边三角形,BD是高,延长BC到点E,使DB=DE,则∠CDE=
.
7.如图,已知△ABC是等边三角形,点B,C,D,F在同一直线上,CD=CE,DF=DG,则∠F= °.
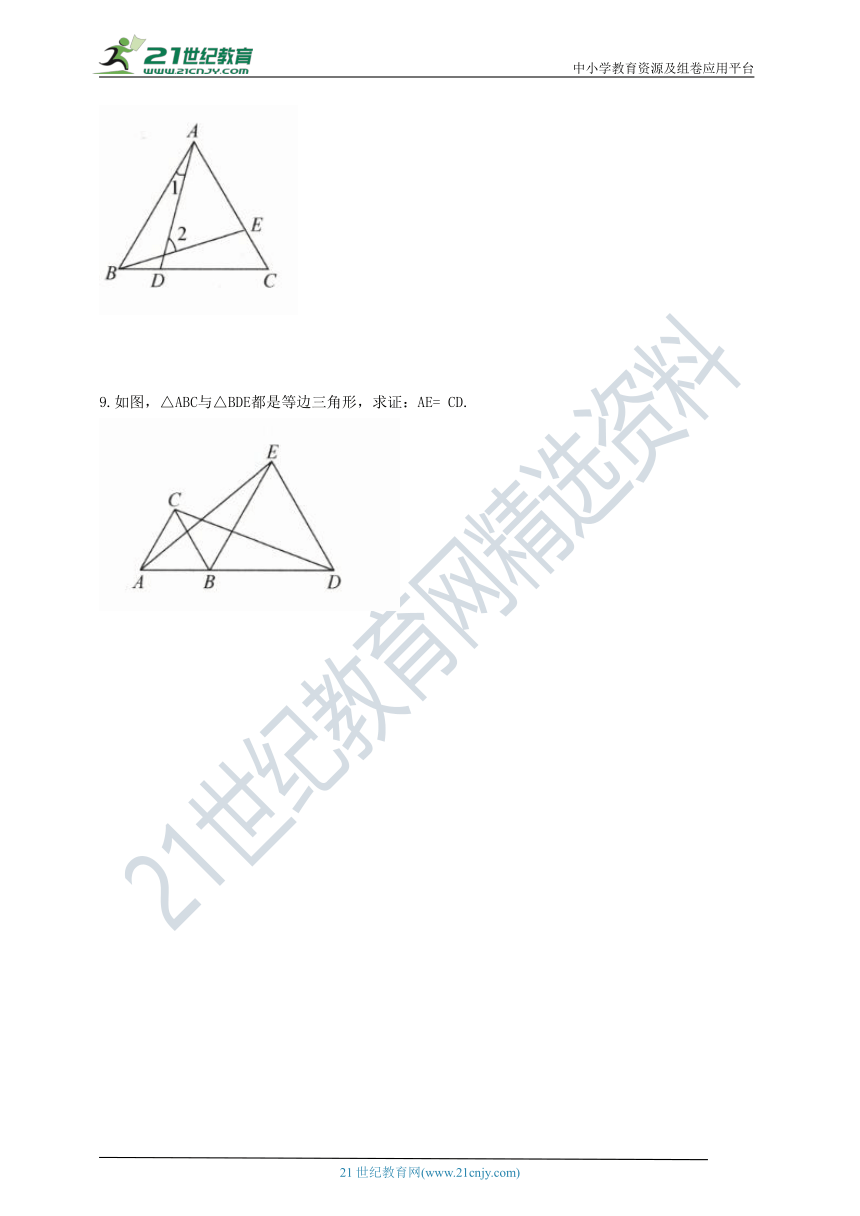
8.如图所示,△ABC是等边三角形,且BD=CE,求∠2的度数.
9.如图,△ABC与△BDE都是等边三角形,求证:AE= CD.
参考答案
1.答案:D
解析:A选项,由BD,CE分别为AC,AB上的高,可判定△BCE≌△CBD,得到BD=CE,不符合题意;B选项,由BD,CE分别为∠ABC,∠ACB的平分线,可判定△BCE≌△CBD,得到BD=CE,不符合题意;C选项,由∠ABD=∠ABC,∠ACE=∠ACB,可得∠DBC=∠ECB,可判定△BCE≌△CBD,得到BD=CE,不符合题意;D选项,由∠ABD=∠BCE,不能判定△BCE≌△CBD,得不到BD=CE,符合题意.故选D.
2.答案:BM=DE+DF.
解析:因为,∴AC·BM=AB·DE+AC·DF.∵AB=AC,∴BM=DE+DF.
3.答案:C
解析:∵△ABC是等边三角形,AB=4,∴AC=AB=4.∵BD⊥AC,∴AD=AC=.故选C.
4.答案:A
解析:如图,在等边三角形ABC中,AB=2,过点A作AD⊥BC于点D.
∵等边三角形高线即中线,∴BD=CD=1.在Rt△ABD中,AB=2,BD=1,
∴AD=,∴等边三角形ABC的面积为BC·AD=.故选A.
5.答案:B
解析:如图,∵∠3+∠6+60°=180°,∠2+∠4+60°=180°,∠1+∠5+60°=180°,∴.∠1+∠2+∠3+∠4+∠5+∠6=540°-180°=360°.又∵∠4+∠5+∠6=180°,∴∠1+∠2+∠3=180°,∴∠3=180°-(∠1+∠2)=60°.故选B.
6.答案:30°
解析:∵△ABC是等边三角形,BD是高,∴∠ABC=∠ACB=60°,∴∠DBC=∠ABC=30°.又∵DB=DE,∴∠E=∠DBC=30°,∴∠CDE=∠ACB-∠E=60°-30°=30°.
7.答案:15
解析:∵△ABC是等边三角形,∴∠ACB=60°,∴∠ACD=120°.∵CE=CD,∴∠CDE=30°,∴∠FDG=150°.∵DF=DG,∴∠F=15°.故答案为15.
8.答案:∵△ABC是等边三角形,∴AB=BC,∠ABC=∠BCE=60°.∵BD=CE,∴△ABD≌△BCE,∴∠1=∠CBE.∵∠2=∠1+∠ABE,∴∠2=∠CBE+∠ABE=∠ABC=60°.
解析:
9.答案:证明:
∵△ABC与△BDE都是等边三角形,∴∠ABC=∠EBD=60°,AB=BC,EB=BD,∴∠ABC+∠CBE=∠EBD+∠CBE,即∠ABE=∠CBD.在△ABE和△CBD中,∴△ABE≌△CBD(SAS),∴AE=CD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
《1.1.2等边三角形的性质》
知识点一 等腰三角形中的相等线段
1.如图,在△ABC中,AB=AC,下列条件中,不能使BD=CE的是( )
A.BD,CE分别为AC,AB上的高
B.BD,CE分别为∠ABC,∠ACB的平分线
C.∠ABD=∠ABC,∠ACE=∠ACB
D.∠ABD=∠BCE
2.如图,在△ABC中,AB=AC,D为BC上的一点,连接AD,DE⊥AB于点E,DF⊥AC于点F,BM为AC边上的高,试探索DE+DF与BM的大小关系.
知识点二 等边三角形的性质
3.如图,△ABC是等边三角形,BD⊥AC于点D,若AB=4,则AD的长为( )
A.1
B.1.5
C.2
D.2.5
4.等边三角形的边长为2,则该等边三角形的面积是( )
A.
B.2
C.1
D.
5.三个等边三角形的摆放位置如图所示,若∠1+∠2=120°,则∠3的度数为( )
A.90°
B.60°
C.45°
D.30°
6.如图,△ABC是等边三角形,BD是高,延长BC到点E,使DB=DE,则∠CDE=
.
7.如图,已知△ABC是等边三角形,点B,C,D,F在同一直线上,CD=CE,DF=DG,则∠F= °.
8.如图所示,△ABC是等边三角形,且BD=CE,求∠2的度数.
9.如图,△ABC与△BDE都是等边三角形,求证:AE= CD.
参考答案
1.答案:D
解析:A选项,由BD,CE分别为AC,AB上的高,可判定△BCE≌△CBD,得到BD=CE,不符合题意;B选项,由BD,CE分别为∠ABC,∠ACB的平分线,可判定△BCE≌△CBD,得到BD=CE,不符合题意;C选项,由∠ABD=∠ABC,∠ACE=∠ACB,可得∠DBC=∠ECB,可判定△BCE≌△CBD,得到BD=CE,不符合题意;D选项,由∠ABD=∠BCE,不能判定△BCE≌△CBD,得不到BD=CE,符合题意.故选D.
2.答案:BM=DE+DF.
解析:因为,∴AC·BM=AB·DE+AC·DF.∵AB=AC,∴BM=DE+DF.
3.答案:C
解析:∵△ABC是等边三角形,AB=4,∴AC=AB=4.∵BD⊥AC,∴AD=AC=.故选C.
4.答案:A
解析:如图,在等边三角形ABC中,AB=2,过点A作AD⊥BC于点D.
∵等边三角形高线即中线,∴BD=CD=1.在Rt△ABD中,AB=2,BD=1,
∴AD=,∴等边三角形ABC的面积为BC·AD=.故选A.
5.答案:B
解析:如图,∵∠3+∠6+60°=180°,∠2+∠4+60°=180°,∠1+∠5+60°=180°,∴.∠1+∠2+∠3+∠4+∠5+∠6=540°-180°=360°.又∵∠4+∠5+∠6=180°,∴∠1+∠2+∠3=180°,∴∠3=180°-(∠1+∠2)=60°.故选B.
6.答案:30°
解析:∵△ABC是等边三角形,BD是高,∴∠ABC=∠ACB=60°,∴∠DBC=∠ABC=30°.又∵DB=DE,∴∠E=∠DBC=30°,∴∠CDE=∠ACB-∠E=60°-30°=30°.
7.答案:15
解析:∵△ABC是等边三角形,∴∠ACB=60°,∴∠ACD=120°.∵CE=CD,∴∠CDE=30°,∴∠FDG=150°.∵DF=DG,∴∠F=15°.故答案为15.
8.答案:∵△ABC是等边三角形,∴AB=BC,∠ABC=∠BCE=60°.∵BD=CE,∴△ABD≌△BCE,∴∠1=∠CBE.∵∠2=∠1+∠ABE,∴∠2=∠CBE+∠ABE=∠ABC=60°.
解析:
9.答案:证明:
∵△ABC与△BDE都是等边三角形,∴∠ABC=∠EBD=60°,AB=BC,EB=BD,∴∠ABC+∠CBE=∠EBD+∠CBE,即∠ABE=∠CBD.在△ABE和△CBD中,∴△ABE≌△CBD(SAS),∴AE=CD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
