1.3.1_线段的垂直平分线 基础训练(含答案)
文档属性
| 名称 | 1.3.1_线段的垂直平分线 基础训练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 21:43:37 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《1.3.1线段的垂直平分线》
知识点一 线段的垂直平分线的性质
1.如图,在△ABC中,边AB的垂直平分线分别交AB,BC于点D,E,边AC的垂直平分线分别交AC,BC于点F,G.若△AEG的周长为8,则BC长是( )
A.12
B.8
C.6
D.4
2.如图,在△ABC中,∠C=90°,AB边的垂直平分线交BC于点D.若BC=8,AD=5,则AC等于 .
3.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE,FG分别为AB,AC的垂直平分线,EG分别为垂足.
(1)直接写出∠BAC的度数;
(2)求∠DAF的度数.
知识点二 线段的垂直平分线的判定
4.若P是△ABC所在平面内的点,且PA=PB=PC,则下列说法正确的是( )
A.点P是△ABC三边垂直平分线的交点
B.点P是△ABC三条角平分线的交点
C.点P是△ABC三边上高的交点
D.点P是△ABC三边中线的交点
5.如图,AC=AD,BC=BD,则有( )
A.AB与CD互相垂直平分
B.CD垂直平分AB
C.AB垂直平分CD
D.CD平分∠ACB
6.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,连接BE,CD相交于点F,求证:BE垂直平分CD.
易错点 不注意运用分类讨论思想,漏掉某些符合条件的情况或结论
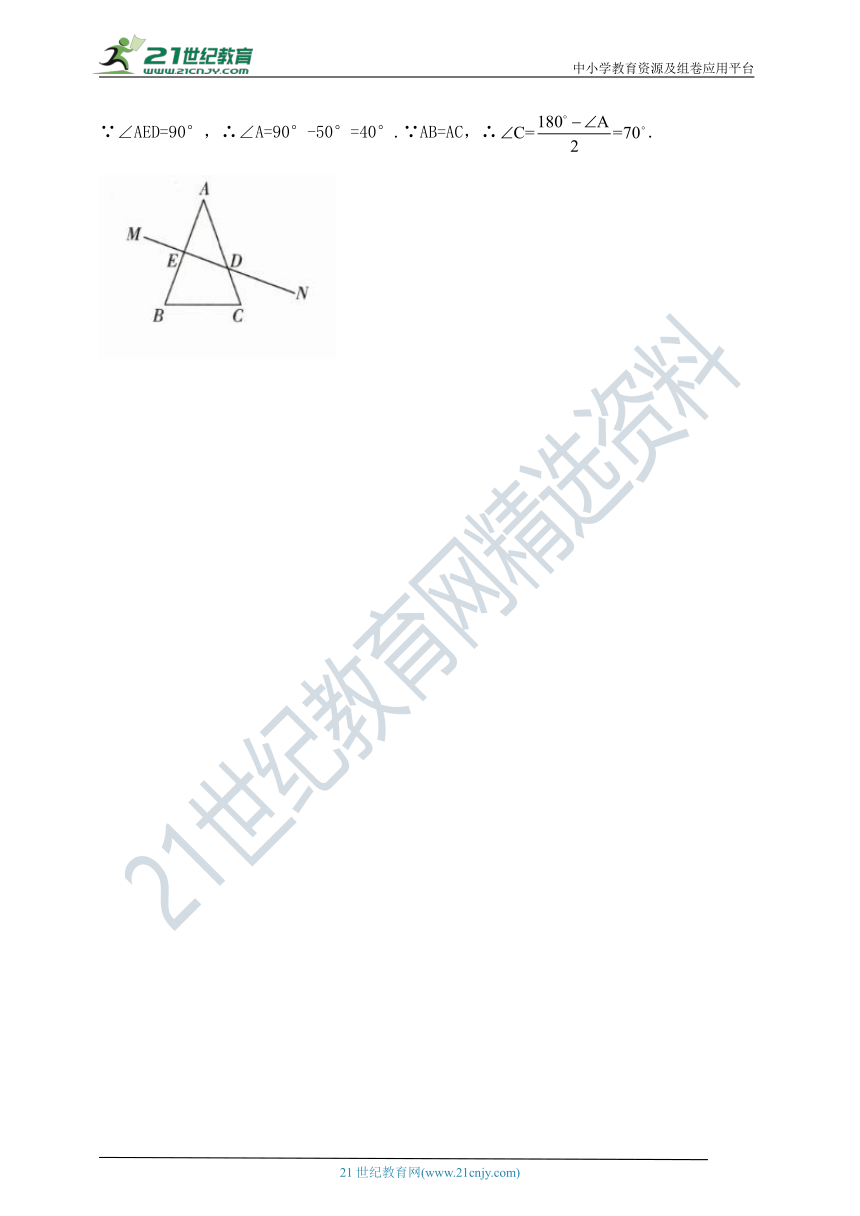
7.在△ABC中,AB=AC,AB的垂直平分线与边AC所在的直线相交所得的锐角为50°,求∠C的度数.
佳琪给出了下面的解题过程,请判断解题过程是否正确,如果不正确,请写出正确的解题过程.
解:如图,当AB的垂直平分线MN与AC相交时,
∵∠AED=90°,∴∠A=90°-50°=40°.∵AB=AC,∴.
参考答案
1.答案:B
解析:∵DE是AB边的垂直平分线,GF是AC边的垂直平分线,∴EB=EA,GA=GC,∴△AEG的周长为AE+EG+AG=BE+EG+GC=BC=8.故选B.
2.答案:4
解析:∵AB边的垂直平分线交BC于点D,AD=5,∴BD=AD=5.∵BC=8,∴CD=BC-BD=3,∴AC==4.
3.答案:(1)∵∠ABC+∠ACB+∠BAC=180°,∴∠BAC=180°-30°-50°=100°.
(2)∵DE是线段AB的垂直平分线,∴DA=DB,∴∠DAB=∠ABC=30°.同理可得∠FAC=∠ACB=50°,∴∠DAF=∠BAC-∠DAB-∠FAC=100°-30°-50°=20°.
解析:
4.答案:A
解析:∵PA=PB,∴点P在线段AB的垂直平分线上.∵PB=PC,∴点P在线段BC的垂直平分线上,∵PA=PC,∴点P在线段AC的垂直平分线上,∴点P是△ABC三边垂直平分线的交点,故选A.
5.答案:C
解析:∵AC=AD,BC=BD,AB垂直平分CD.故选C.
6.答案:【证明】∵∠ACB=90°,DE⊥AB,∴∠ACB=∠BDE=90°.在Rt△BDE和Rt△BCE中,∴Rt△BDE≌Rt△BCE(HL),∴ED=EC,∴点E在CD的垂直平分线上.∵BD=BC,∴点B在CD的垂直平分线上,∴BE垂直平分CD.
解析:
7.答案:佳琪的解题过程不正确.正确的解题过程如下:
如图(1),当AB的垂直平分线MN与AC相交时,∵∠AED=90°,∴∠A=90°-50°=40°.∵AB=AC,∴∠C= 70°;
②如图(2),当AB的垂直平分线MN与CA的延长线相交时,则∠DAB=90°-50°=40°.∵AB=AC,∴∠C=∠DAB=20°.综上所述,∠C的度数为20°或70°.
解析:易错警示 解决这类问题时,一定要考虑所有可能的情况,进行分类讨论,切不可因遗漏其中一种情况而致错.
_21?????????è?????(www.21cnjy.com)_
《1.3.1线段的垂直平分线》
知识点一 线段的垂直平分线的性质
1.如图,在△ABC中,边AB的垂直平分线分别交AB,BC于点D,E,边AC的垂直平分线分别交AC,BC于点F,G.若△AEG的周长为8,则BC长是( )
A.12
B.8
C.6
D.4
2.如图,在△ABC中,∠C=90°,AB边的垂直平分线交BC于点D.若BC=8,AD=5,则AC等于 .
3.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE,FG分别为AB,AC的垂直平分线,EG分别为垂足.
(1)直接写出∠BAC的度数;
(2)求∠DAF的度数.
知识点二 线段的垂直平分线的判定
4.若P是△ABC所在平面内的点,且PA=PB=PC,则下列说法正确的是( )
A.点P是△ABC三边垂直平分线的交点
B.点P是△ABC三条角平分线的交点
C.点P是△ABC三边上高的交点
D.点P是△ABC三边中线的交点
5.如图,AC=AD,BC=BD,则有( )
A.AB与CD互相垂直平分
B.CD垂直平分AB
C.AB垂直平分CD
D.CD平分∠ACB
6.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,连接BE,CD相交于点F,求证:BE垂直平分CD.
易错点 不注意运用分类讨论思想,漏掉某些符合条件的情况或结论
7.在△ABC中,AB=AC,AB的垂直平分线与边AC所在的直线相交所得的锐角为50°,求∠C的度数.
佳琪给出了下面的解题过程,请判断解题过程是否正确,如果不正确,请写出正确的解题过程.
解:如图,当AB的垂直平分线MN与AC相交时,
∵∠AED=90°,∴∠A=90°-50°=40°.∵AB=AC,∴.
参考答案
1.答案:B
解析:∵DE是AB边的垂直平分线,GF是AC边的垂直平分线,∴EB=EA,GA=GC,∴△AEG的周长为AE+EG+AG=BE+EG+GC=BC=8.故选B.
2.答案:4
解析:∵AB边的垂直平分线交BC于点D,AD=5,∴BD=AD=5.∵BC=8,∴CD=BC-BD=3,∴AC==4.
3.答案:(1)∵∠ABC+∠ACB+∠BAC=180°,∴∠BAC=180°-30°-50°=100°.
(2)∵DE是线段AB的垂直平分线,∴DA=DB,∴∠DAB=∠ABC=30°.同理可得∠FAC=∠ACB=50°,∴∠DAF=∠BAC-∠DAB-∠FAC=100°-30°-50°=20°.
解析:
4.答案:A
解析:∵PA=PB,∴点P在线段AB的垂直平分线上.∵PB=PC,∴点P在线段BC的垂直平分线上,∵PA=PC,∴点P在线段AC的垂直平分线上,∴点P是△ABC三边垂直平分线的交点,故选A.
5.答案:C
解析:∵AC=AD,BC=BD,AB垂直平分CD.故选C.
6.答案:【证明】∵∠ACB=90°,DE⊥AB,∴∠ACB=∠BDE=90°.在Rt△BDE和Rt△BCE中,∴Rt△BDE≌Rt△BCE(HL),∴ED=EC,∴点E在CD的垂直平分线上.∵BD=BC,∴点B在CD的垂直平分线上,∴BE垂直平分CD.
解析:
7.答案:佳琪的解题过程不正确.正确的解题过程如下:
如图(1),当AB的垂直平分线MN与AC相交时,∵∠AED=90°,∴∠A=90°-50°=40°.∵AB=AC,∴∠C= 70°;
②如图(2),当AB的垂直平分线MN与CA的延长线相交时,则∠DAB=90°-50°=40°.∵AB=AC,∴∠C=∠DAB=20°.综上所述,∠C的度数为20°或70°.
解析:易错警示 解决这类问题时,一定要考虑所有可能的情况,进行分类讨论,切不可因遗漏其中一种情况而致错.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
