1.3.2_三角形三边垂直平分线的性质及应用 基础训练(含解析)
文档属性
| 名称 | 1.3.2_三角形三边垂直平分线的性质及应用 基础训练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《1.3.2三角形二边垂直平分线的性质及应用》
知识点一 三角形三边垂直平分线的性质
1.如图,兔子的三个洞口A,B,C构成△ABC,猎狗想到三个洞口的距离都相等处捕捉兔子,则猎狗应蹲守在( )
A.三条边的垂直平分线的交点
B.三个角的角平分线的交点
C.三角形三条高的交点
D.三角形三条中线的交点
2.如果一个三角形的两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.不能确定
3.如图,∠A=80°,点O是AB,AC的垂直平分线的交点,则∠BCO的度数是( )
A.40°
B.30°
C.20°
D.10°
4.如图,在△ABC中,AB边的垂直平分线交BC于点D,AC边的垂直平分线交BC于点E,与相交于点O,连接OB,OC,OA.若△ADE的周长为6 cm,△OBC的周长为16 cm.求线段OA的长.
知识点二 利用线段垂直平分线的性质尺规作图
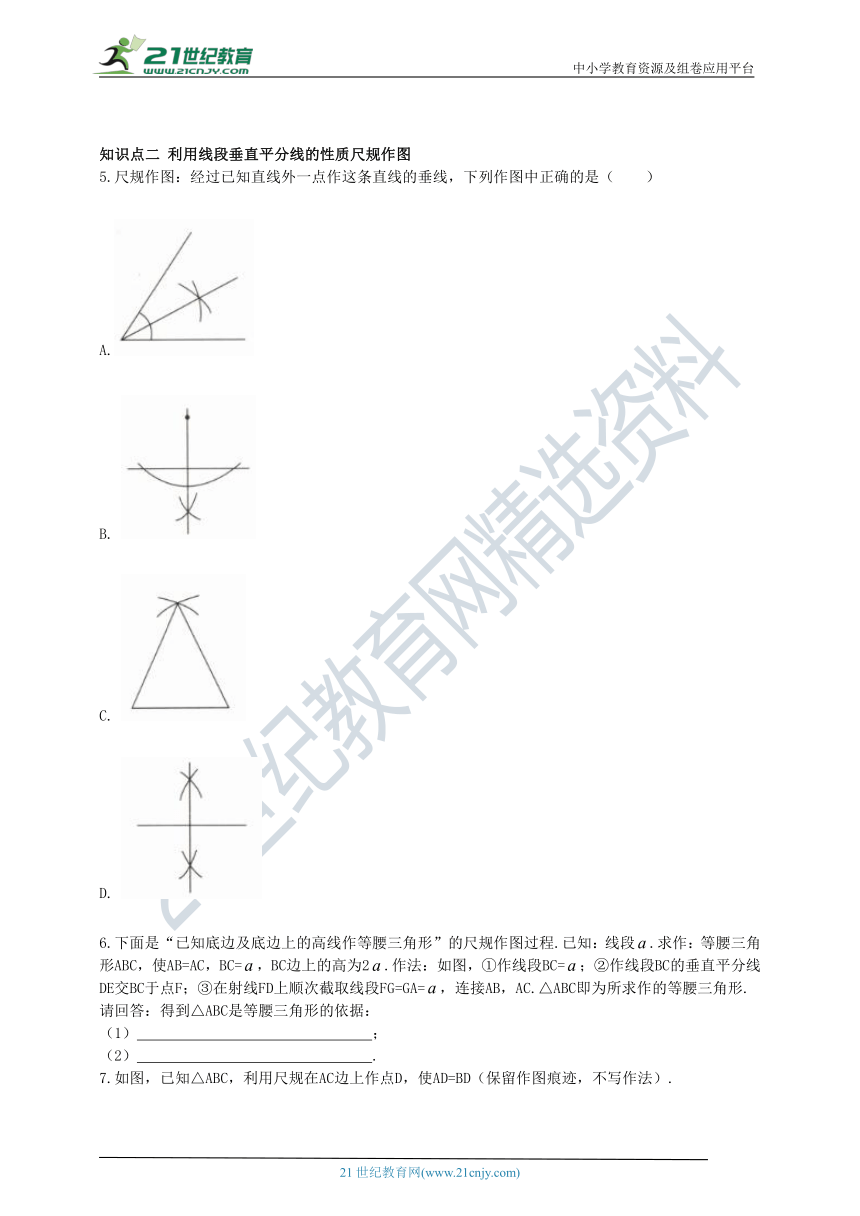
5.尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是( )
A.
B.
C.
D.
6.下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.已知:线段.求作:等腰三角形ABC,使AB=AC,BC=,BC边上的高为2.作法:如图,①作线段BC=;②作线段BC的垂直平分线DE交BC于点F;③在射线FD上顺次截取线段FG=GA=,连接AB,AC.△ABC即为所求作的等腰三角形.
请回答:得到△ABC是等腰三角形的依据:
(1) ;
(2) .
7.如图,已知△ABC,利用尺规在AC边上作点D,使AD=BD(保留作图痕迹,不写作法).
8.如图,在公路l的同侧有两个居民点A,B,现要在公路边上修一个污水处理站P来收集处理居民点A,B的污水,污水处理站P修在什么地方到居民点A,B所用的水管最短?请你在图中找出污水处理站P的位置.(保留作图痕迹,不写作法)
9.通过文明城市的评选,人们增强了卫生意识,大街上随地乱扔生活垃圾的人少了,人们自觉地将生活垃圾倒入垃圾桶中.如图所示,A,B,C为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,要使得垃圾回收站建在到三个小区距离都相等的某处,如果你是工程师,请你在图
中确定出垃圾回收站的位置.
参考答案
1.答案:A
解析:猎狗到△ABC三个顶点的距离相等,则猎狗应蹲守在△ABC的三条边垂直平分线的交点.故选A.
2.答案:C
解析:如图,CA,CB的垂直平分线OD,OE相交于点O,且点O落在AB边上.连接CO.∵OD是AC的垂直平分线,∴OC=OA,∴∠A=∠OCA.同理可得∠B=∠OCB.∵在△ABC中,∠A+∠OCA+∠OCB+∠B=180°,即2(∠OCA+∠OCB)=180°,∴∠ACB=90°,∴△ABC是直角三角形.故选C.
3.答案:D
解析:如图,连接OA,OB.∵∠BAC=80°,∴∠ABC+∠ACB=100°.∵点O是AB,AC的垂直平分线的交点,∴OA=OB,OA=OC,∴∠OAB=∠OBA,∠OCA=∠OAC,OB=OC,∴∠OBA+∠OCA=80°,∴∠OBC+∠OCB=100°-80°=20°.∵OB=OC,∴∠BCO=∠CBO=10°.故选D.
4.答案:∵是AB边的垂直平分线,∴DA=DB,OA=OB.∵是AC边的垂直平分线,∴EA=EC,OA=OC,∴OB=OC =OA.,∴BC= BD +DE +EC= DA +DE +EA=6 cm.∵OB +OC +BC= 16 cm. ∴OA=OB=OC=5 cm.
解析:
5.答案:B
解析:如图,已知:直线AB和AB外一点C.求作:AB的垂线,使它经过点C.作法:①任意取一点K,使点K和点C在AB的两旁.②以点C为圆心,CK的长为半径作弧,交AB于点D,E.③分别以点D,E为圆心,大于DE长为半径作弧,两弧交于点F.④作直线CF.直线CF.就是所求的垂线.故选B.
6.答案:(1)线段垂直平分线上的点到线段两个端点的距离相等
(2)有两条边相等的三角形是等腰三角形
解析:由作图得,DE垂直平分BC,AB=AC.故△ABC是等腰三角形.
7.答案:如图所示,点D即为所求.
解析:
8.答案:【解】如图所示:
解析:
9.答案:【解】如图,连接AB,AC.
①分别以A,B为圆心,大于AB的长为半径画弧,两弧相交于H,D两点,连接HD;
②分别以A,C为圆心,大于AC的长为半径画弧,两弧相交于E,F两点,连接EF;
③HD与EF的交点为G,则点G即为所求.
解析:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
《1.3.2三角形二边垂直平分线的性质及应用》
知识点一 三角形三边垂直平分线的性质
1.如图,兔子的三个洞口A,B,C构成△ABC,猎狗想到三个洞口的距离都相等处捕捉兔子,则猎狗应蹲守在( )
A.三条边的垂直平分线的交点
B.三个角的角平分线的交点
C.三角形三条高的交点
D.三角形三条中线的交点
2.如果一个三角形的两边的垂直平分线的交点在第三边上,那么这个三角形是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.不能确定
3.如图,∠A=80°,点O是AB,AC的垂直平分线的交点,则∠BCO的度数是( )
A.40°
B.30°
C.20°
D.10°
4.如图,在△ABC中,AB边的垂直平分线交BC于点D,AC边的垂直平分线交BC于点E,与相交于点O,连接OB,OC,OA.若△ADE的周长为6 cm,△OBC的周长为16 cm.求线段OA的长.
知识点二 利用线段垂直平分线的性质尺规作图
5.尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是( )
A.
B.
C.
D.
6.下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.已知:线段.求作:等腰三角形ABC,使AB=AC,BC=,BC边上的高为2.作法:如图,①作线段BC=;②作线段BC的垂直平分线DE交BC于点F;③在射线FD上顺次截取线段FG=GA=,连接AB,AC.△ABC即为所求作的等腰三角形.
请回答:得到△ABC是等腰三角形的依据:
(1) ;
(2) .
7.如图,已知△ABC,利用尺规在AC边上作点D,使AD=BD(保留作图痕迹,不写作法).
8.如图,在公路l的同侧有两个居民点A,B,现要在公路边上修一个污水处理站P来收集处理居民点A,B的污水,污水处理站P修在什么地方到居民点A,B所用的水管最短?请你在图中找出污水处理站P的位置.(保留作图痕迹,不写作法)
9.通过文明城市的评选,人们增强了卫生意识,大街上随地乱扔生活垃圾的人少了,人们自觉地将生活垃圾倒入垃圾桶中.如图所示,A,B,C为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,要使得垃圾回收站建在到三个小区距离都相等的某处,如果你是工程师,请你在图
中确定出垃圾回收站的位置.
参考答案
1.答案:A
解析:猎狗到△ABC三个顶点的距离相等,则猎狗应蹲守在△ABC的三条边垂直平分线的交点.故选A.
2.答案:C
解析:如图,CA,CB的垂直平分线OD,OE相交于点O,且点O落在AB边上.连接CO.∵OD是AC的垂直平分线,∴OC=OA,∴∠A=∠OCA.同理可得∠B=∠OCB.∵在△ABC中,∠A+∠OCA+∠OCB+∠B=180°,即2(∠OCA+∠OCB)=180°,∴∠ACB=90°,∴△ABC是直角三角形.故选C.
3.答案:D
解析:如图,连接OA,OB.∵∠BAC=80°,∴∠ABC+∠ACB=100°.∵点O是AB,AC的垂直平分线的交点,∴OA=OB,OA=OC,∴∠OAB=∠OBA,∠OCA=∠OAC,OB=OC,∴∠OBA+∠OCA=80°,∴∠OBC+∠OCB=100°-80°=20°.∵OB=OC,∴∠BCO=∠CBO=10°.故选D.
4.答案:∵是AB边的垂直平分线,∴DA=DB,OA=OB.∵是AC边的垂直平分线,∴EA=EC,OA=OC,∴OB=OC =OA.,∴BC= BD +DE +EC= DA +DE +EA=6 cm.∵OB +OC +BC= 16 cm. ∴OA=OB=OC=5 cm.
解析:
5.答案:B
解析:如图,已知:直线AB和AB外一点C.求作:AB的垂线,使它经过点C.作法:①任意取一点K,使点K和点C在AB的两旁.②以点C为圆心,CK的长为半径作弧,交AB于点D,E.③分别以点D,E为圆心,大于DE长为半径作弧,两弧交于点F.④作直线CF.直线CF.就是所求的垂线.故选B.
6.答案:(1)线段垂直平分线上的点到线段两个端点的距离相等
(2)有两条边相等的三角形是等腰三角形
解析:由作图得,DE垂直平分BC,AB=AC.故△ABC是等腰三角形.
7.答案:如图所示,点D即为所求.
解析:
8.答案:【解】如图所示:
解析:
9.答案:【解】如图,连接AB,AC.
①分别以A,B为圆心,大于AB的长为半径画弧,两弧相交于H,D两点,连接HD;
②分别以A,C为圆心,大于AC的长为半径画弧,两弧相交于E,F两点,连接EF;
③HD与EF的交点为G,则点G即为所求.
解析:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
